-
The search for the Odderon has concentrated for a long time on the difference between particle-particle and antiparticle-particle scattering at high energies. The t dependence of
pp andˉpp elastic collisions was measured at the CERN ISR and SPS [1–3], and a marked difference was found between the differential cross-sections forpp andˉpp elastic collisions at√s = 52.8 GeV.(dσdt)ˉpp is smooth for that momentum transfer, but(dσdt)pp has a characteristic dip around∣t∣ = 1.35 GeV2. The total cross-sectionσpptot and the ratio of the real to imaginary parts of the forward scattering amplitudeρpp at√s = 2.76 TeV, 7 TeV and 8 TeV were measured by the TOTEM collaboration at the LHC [4–9]. Recently, the TOTEM collaboration measured the total cross-sectionσtot = (110.6 ±3.4) mb [10], and the ratio of the real to imaginary parts of the forward scattering amplitudeρ = Re/Im = (0.098 ±0.01) [11] for thepp elastic collisions at√s = 13 TeV. There is some experimental evidence for the Odderon, related to the scattering amplitude with odd parity C = −1 under charge conjugation. In particular, the TOTEM experimental data show a possible contribution of the odd signature amplitude to the total cross-section. Evidence of the Odderon would lead to many interesting aspects of high energy scattering in QCD.Let us make a very short review of the Odderon. Regge proposed a new method for calculating the scattering amplitude in quantum mechanics in 1959 [12, 13]. The Regge theory assumes that the scattering amplitude is an asymptotic function of the center-of-mass energy
√s and four-momentum transfer t. It relates the orbital angular momentum J and the mass M of particles with the same quantum numbers (charge Q, baryon B, strangeness, isospin I, etc.) as J =αR (t = m2), the Regge trajectory [12, 13]. For two-hadron collision process1+2→3+4 , the total cross-section increases slowly with energyσtot(s)∼sαR−1 and should vanish fors→∞ . In fact, the total cross-section does not vanish as the energy increases. The interaction between colliding particles is explained by the exchange between them, the so-called Regge trajectory. In the Pomeron exchange model of the 1960's, the Regge theory framework was widely studied. The Pomeron is different from the intercept (αR⩽1 ) of the Regge trajectory for all existing particles in nature, and its intercept isαP≃ 1.08>1. The Pomeron is assumed to be an object composed of two gluons in a colorless state with a C-parity of C = +1. Hence the Pomeron may have a close relative with a C-parity of C = −1. The relative, the Odderon, was proposed in 1973 by Lukaszuk and Nicolescu [14].QCD is the fundamental theory of the strong interaction. It was discovered in early 1973. In perturbative QCD, the Odderon is considered to be composed of three interacting reggeized gluons in a symmetric color state [15, 16]. In many theories, it is assumed that the Odderon leads to a difference between the total cross-sections of particle-particle and particle-antiparticle collisions, and many models have been proposed [17–24] to explain the experimental data for the
pp andˉpp elastic collisions. Does the Odderon exist? If the existence of the Odderon is experimentally confirmed, it would become a very interesting object in high energy scattering in QCD.We attempt to build a relationship between the Regge theory and the QCD dynamics. We first describe the
pp andˉpp elastic collisions at high energy by using the crossing symmetry and unitarity [25–27]. In Sec. 2, we introduce a very important consequence of analyticity - the crossing symmetry - and present the related formalism of the total cross-sectionσtot and the ratio of the real to imaginary parts of the forward scattering amplitudeρ in the FPO mode1. In Sec. 3, we give our theoretical predictions and a comparison with the TOTEM experimental results. A comparison with other calculations of the Odderon intercept is given in Sec. 4. Our summary and concluding remarks are presented in Sec. 5. -
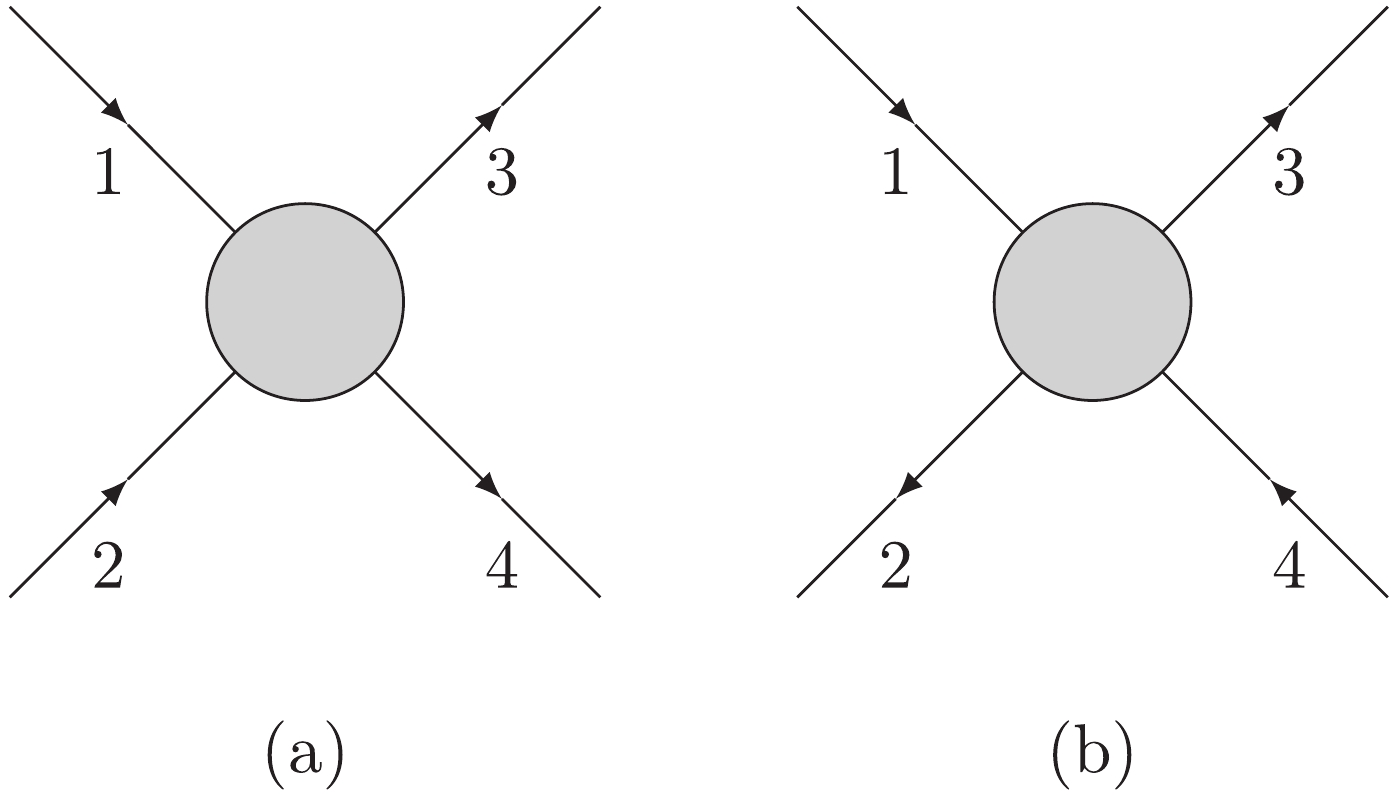
In quantum field theory, the amplitude of the two-to-two elastic collisions process in the u-channel
1+ˉ4→3+ˉ2 (Fig. 1(b)) can be obtained from the amplitude of the two-to-two elastic collisions process in the s -channel1+2→3+4 (Fig. 1(a)). As a consequence of analyticity - the crossing symmetry relationship - we haveF1+ˉ4→3+ˉ2(s,t,u)=F1+2→3+4(u,t,s).

(1) The fermion-antifermion elastic collision with an amplitude
F1+ˉ2→1+ˉ2(s,t) can be obtained from the fermion-fermion elastic collision with an amplitudeF1+2→1+2(s,t) by crossing to the u-channelF1+ˉ2→1+ˉ2(s,t)=F1+2→1+2(s,t).

(2) Let us now define two new amplitudes
F± usingF12(s,t) andF1ˉ2(s,t) such thatF±(s,t)=12(F12(s,t)±F1ˉ2(s,t)),

(3) F12(s,t)=F+(s,t)+F−(s,t),

(4) F1ˉ2(s,t)=F+(s,t)−F−(s,t).

(5) For fermion-fermion and fermion-antifermion elastic collisions, the amplitude
F+ is the same. It has an even (or positive) C-parity, C = +1. It is considered that its main contribution is from the Froissart bound, a Reggeon-Pomeron exchange at high energy. The amplitudeF− changes sign from fermion-fermion to fermion-antifermion elastic collisions, and corresponds to an odd (or negative) C-parity, C = −1. It is dominated by the Odderon exchange and its contribution does not decrease rapidly at high energy.F+ andF− are called even and odd amplitudes under the crossing symmetry. -
Proton is a compound fermion. The proton-proton and proton-antiproton elastic collision process satisfies the crossing symmetry in quantum field theory.
Let us now define two amplitudes
F± for thepp andˉpp elastic collisionsF±(s,t)=12(Fpp(s,t)±Fˉpp(s,t)).

(6) From Eq. (6), we get the following expressions for the amplitudes of
pp andˉpp elastic collisions composed of the even amplitudeF+ and the odd amplitudeF− under the crossing symmetry asFpp(s,t)=F+(s,t)+F−(s,t),

(7) Fˉpp(s,t)=F+(s,t)−F−(s,t).

(8) -
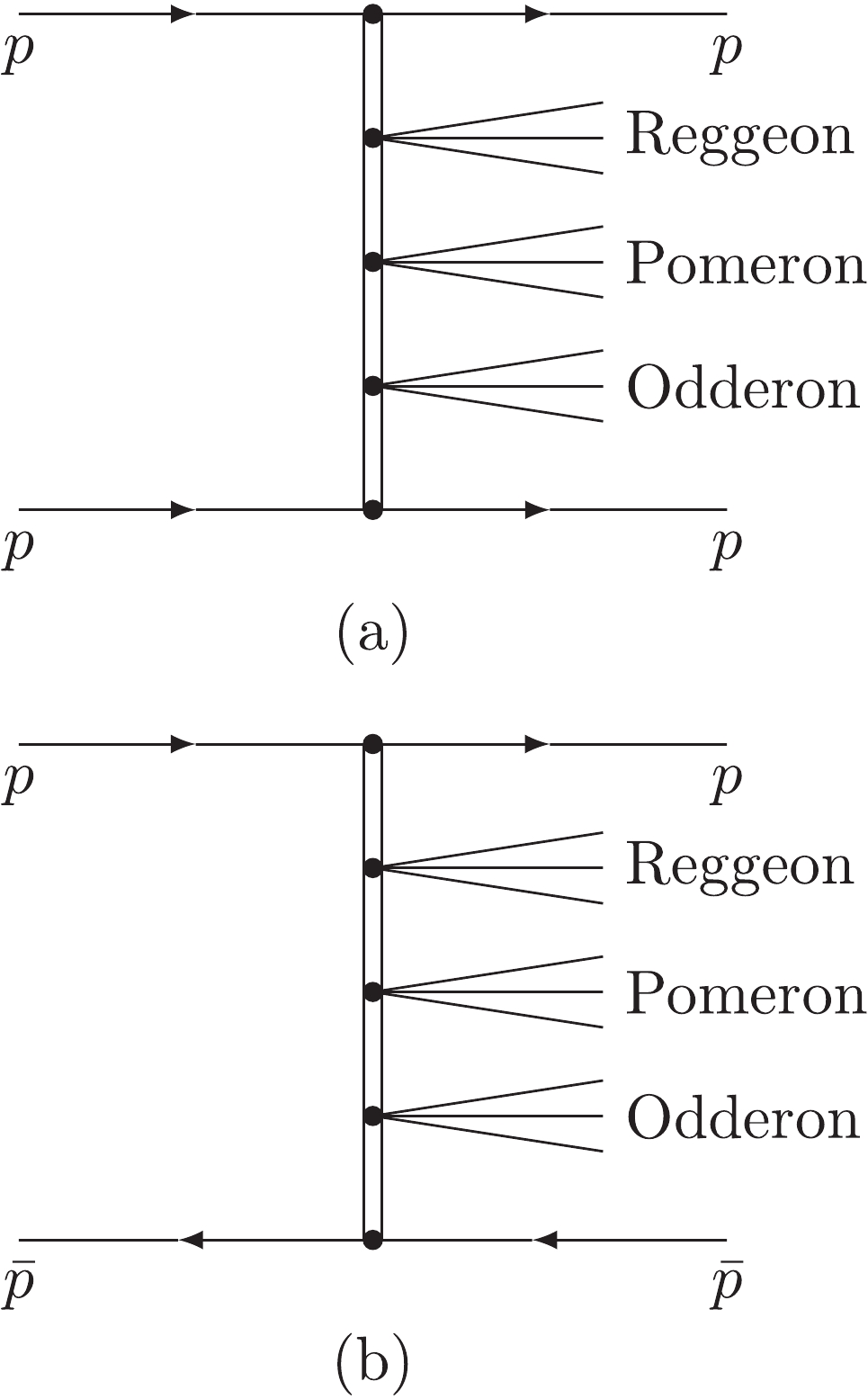
In the 1960's, the process
pp→p+X1+X2+⋯(groups ofparticles)+p , has been recognized [28, 29] as shown in Fig. 2(a, b).Large rapidity gaps (LRG) separate small groups of particles (Xi). These groups of particles may be Reggeons, Pomerons and Odderons. The gaps between them may cause a problem of unitarity.
A consequence of unitarity is the Froissart-Martin theorem [25, 26]. The total hadronic cross-section grows as a logarithm of energy. Specifically
σtot⩽πm2πlog2(ss0),

(9) where
s0 is a free parameter,˜s=ss0 , The usual Froissart bound coefficient ism2π ,1m2π=20mb . The total hadronic cross-section rapidly increases and is 10 barns at the LHC energy.In the Regge theory [12, 13], the scattering amplitude F(s,t) for the process
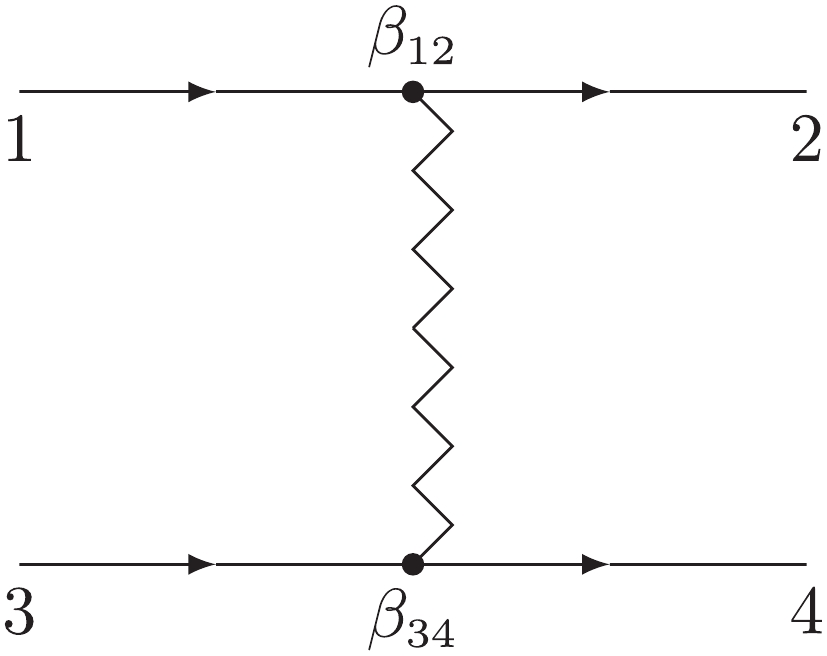
1+2→3+4 can be expressed byα(t) asF1+2→3+4=η+e−iπα(t)2β(t)⋅sα(t).

(10) β(t) in Eq. (10) is a product of two factors which depend only on the coupling of the exchanged object to the scattering particles, as shown in Fig. 3.β(t)=β12(t)β34(t),

(11) α(t)=α0+α′t.

(12) α(t) in Eq. (10) is the Regge trajectory of a particle;α0 is the intercept of the particle trajectory, andα ' its slope.We define our Froissart Pomeron Odderon model (FPO) such that the contributions of the Froissart bound and of the Pomeron, Reggeon and Odderon exchange are taken into account in the forward amplitude
F(s,t) of thepp andˉpp elastic collisions.The even forward amplitudes
F+ of thepp andˉpp elastic collisions are given as the sum of three parts: the first part,FH+ , saturates at the asymptotic bound of the Froissart-Martin theorem. The second partFP+ , is given by the Pomeron pole with an intercept of about 1. The third part,FR+ , describes the conventional Regge poles and cuts.F+=FH++FP++FR+.

(13) FH+ in Eq. (13) denotes the contribution of the Froissart bound to the forward scattering amplitude of thepp andˉpp elastic collisions. The capital H is for "Heisenberg".1isFH+(s,t)=Aln2ˉs2J1(K+ˉτ)K+ˉτexp(b+1t)+BlnˉsJ0(K+ˉτ)exp(b+2t)+H[J0(K+ˉτ)−(K+ˉτ)J1(K+ˉτ)]exp(b+3t),

(14) where
J0,J1 are the Bessel functions, and A, B, H,K+ andbk(k=1,2,3) are constants.ˉs=ss0exp(−12iπ),withs0=1GeV2,

(15) ˉτ=√−tt0lnˉs,witht0=1GeV2.

(16) FP+ andFR+ in Eq. (13) denote the Pomeron and Reggeon contributions to the forward scattering amplitude of thepp andˉpp elastic collisions, and are expressed as:1sFP+(s,t)=Cexp(βPt)[i−cot(π2αP(t))](ss0)(αP(t)−1).

(17) αP(t)=αP(0)+α′Pt,

(18) with
αP(0)=1andα′P=0.25GeV−2,

(19) 1sFR+(s,t)=Dexp(βRt)×[isin(π2αR(t))−cos(π2αR(t))](ss0)(αR(t)−1).

(20) αR(t)=αR(0)+α′Rt,

(21) with
αR(0)=0.5,

(22) where C, D,
βP andβR are constants.The conventional odd forward scattering amplitude of the
pp andˉpp elastic collisions in Regge theory is obtained by the Odderon exchangeF−=FO−.

(23) 1sFO−(s,t)=Eexp(βOt)×[sin(π2αO(t))+icos(π2αO(t))](ss0)(αO(t)−1),

(24) where E and
βO are constants, andαO(t)=αO(0)+α′Ot,

(25) with
αO(0)=0.5.

(26) -
Based on the optical theorem for purely elastic collisions, the total cross-section is related to the elastic forward scattering amplitude
F(s,t=0) σtot=1sImF(s,t=0).

(27) We can then obtain the even and odd cross-sections under the crossing symmetry from the even and odd forward scattering amplitudes
F+ andF− :σeven=1sImF+(s,t=0),

(28) σodd=1sImF−(s,t=0).

(29) The total cross-section for the
pp andˉpp elastic collisions is composed of even and odd cross-sections under the crossing symmetry:σpptot=σeven+σodd,

(30) σˉpptot=σeven−σodd.

(31) The Froissart bound contribution to the total cross-section for the
pp andˉpp elastic collisions can now be written as:σH=Aln2˜s+Bln˜s.

(32) The Pomeron, Reggeon and Odderon exchange terms in the scattering amplitude lead to the cross-section expressed by the Pomeron, Reggeon and Odderon trajectory as
σP∝(s)αP(0)−1,withαP(0)=1,

(33) σR∝(s)αR(0)−1,withαR(0)=0.5.

(34) Here,
αP(0) andαR(0) are the intercepts of the Pomeron trajectoryαP(t) and Reggeon trajectoryαR(t) .The Odderon exchange contribution to the total cross-section of the
pp andˉpp elastic collisions contains the odd forward amplitudeF− , and is given byσO∝(s)αO(0)−1,withαO(0)=0.5,

(35) αO(0) is the intercept of the Odderon trajectoryαO(t) .The difference between the total cross-sections of the
pp andˉpp elastic collisions is the Odderon term, which is due to the odd forward scattering amplitude. In other words, the odd cross-sections of thepp andˉpp elastic collisions change sign under the crossing symmetry. The even and odd cross-sections can be written asσeven=1sIm[FH++FP++FR+]=Imi{A[lnss0−iπ2]2+B[lnss0−iπ2]}+C(ss0)αP(0)−1+Dsin(π2αR(0))(ss0)αR(0)−1,

(36) σodd=1sImFO−=Ecos(π2αO(0))(ss0)αO(0)−1.

(37) The corresponding total cross-sections
σtot can be rewritten respectively asσpptot=σeven+σodd=A[ln2(ss0)−π24]+Blnss0+C(ss0)αP(0)−1+Dsin(π2αR(0))(ss0)αR(0)−1+Ecos(π2αO(0))(ss0)αO(0)−1,

(38) σˉpptot=σeven−σodd=A[ln2(ss0)−π24]+Blnss0+C(ss0)αP(0)−1+Dsin(π2αR(0))(ss0)αR(0)−1−Ecos(π2αO(0))(ss0)αO(0)−1.

(39) The ratio of the real to imaginary parts of the forward scattering amplitude
ρ(s) is defined as [30],ρ(s)=ReF(s,t=0)ImF(s,t=0).

(40) In the FPO model, it can be written for the
pp andˉpp elastic collisions as:ρpp=s[Aπlnss0+Bπ2−Dcos(π2αR(0))(ss0)αR(0)−1−Esin(π2αO(0))(ss0)αO(0)−1]s{A[ln2(ss0)−π24]+Blnss0+C(ss0)αP(0)−1+Dsin(π2αR(0))(ss0)αR(0)−1+Ecos(π2αO(0))(ss0)αO(0)−1},

(41) ρˉpp=s[Aπlnss0+Bπ2−Dcos(π2αR(0))(ss0)αR(0)−1+Esin(π2αO(0))(ss0)αO(0)−1]s{A[ln2(ss0)−π24]+Blnss0+C(ss0)αP(0)−1+Dsin(π2αR(0))(ss0)αR(0)−1−Ecos(π2αO(0))(ss0)αO(0)−1}.

(42) σtot andρ are therefore parametrized in terms of five parameters A, B, C, D and E. -
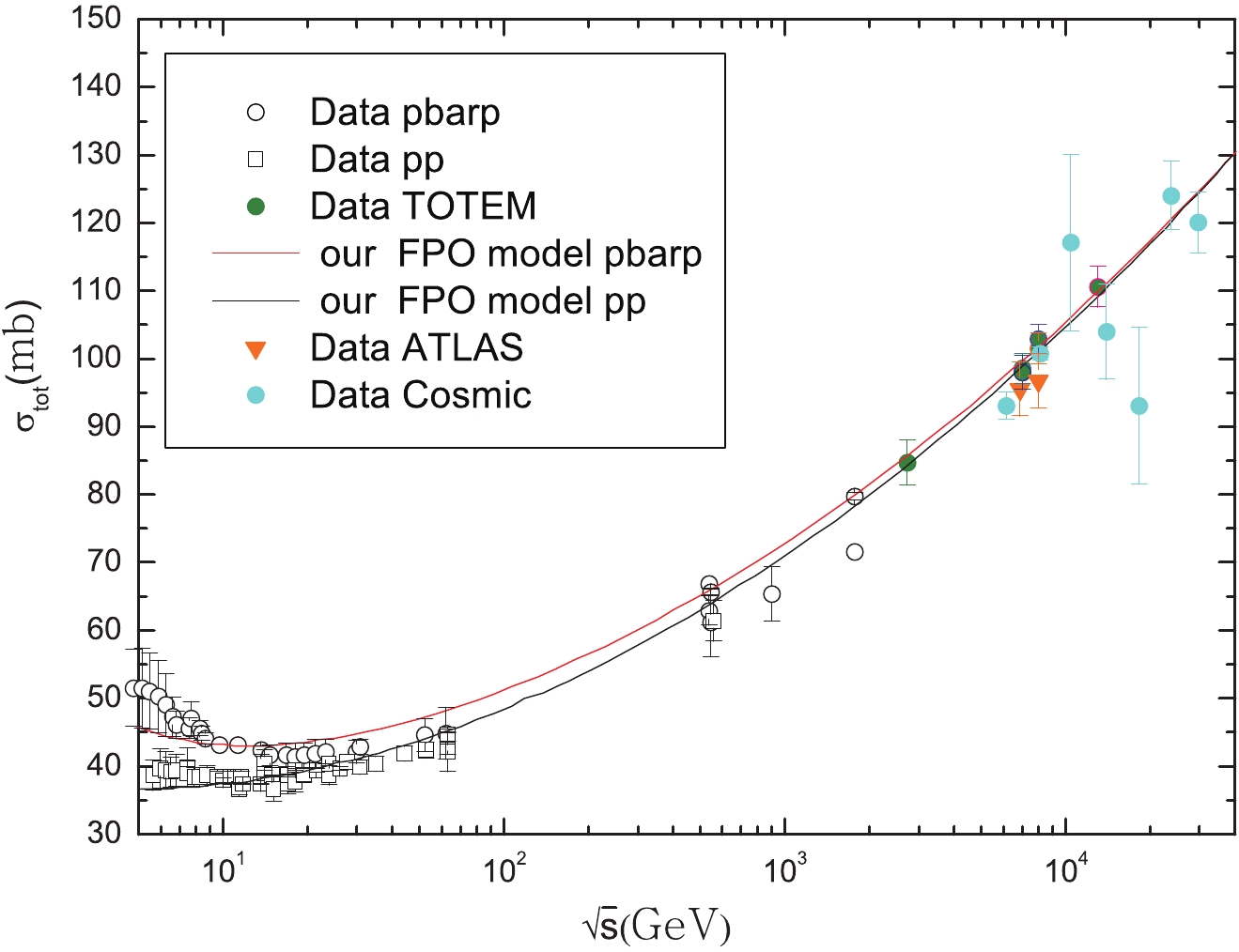
The total cross-section
σtot and the ratio of the real to imaginary parts of the forward scattering amplitudeρ in thepp andˉpp elastic collisions are calculated using the above formulism. The fitted values of the parameters of our FPO model in Eqs. (38, 39, 41, 42) are given in Table 1. Comparison between our theoretical predictions and the experimental data are shown in Fig. 4 and Fig. 5.parameters/mb fitted number error A 0.25 ±0.05 B 0.1964 ±0.0056 C 38.0 ±1.6 D 48.0 ±10.0 E 40.2910 ±2.0005 Table 1. The fit values of the parameters used in the FPO model.
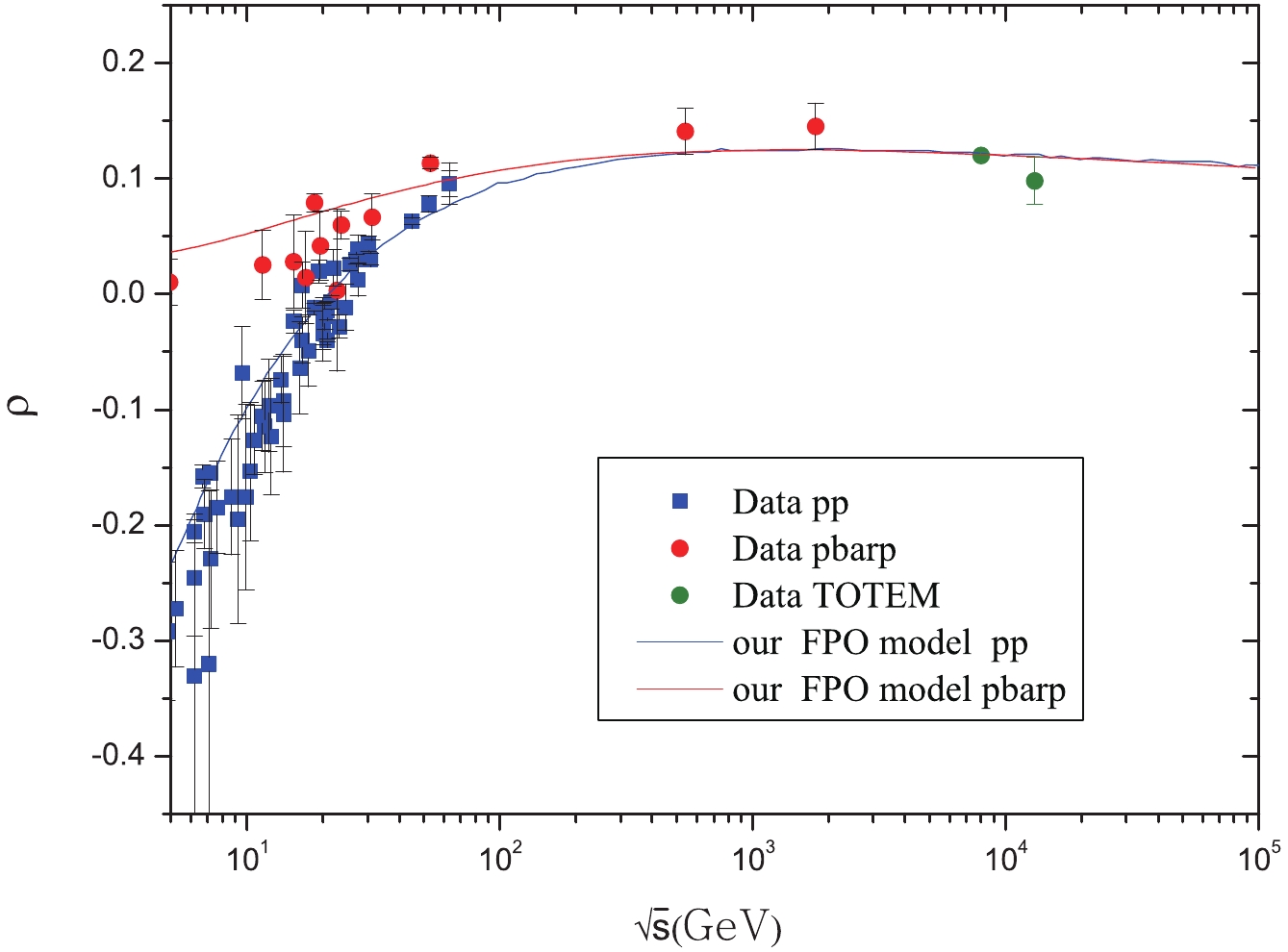
Figure 5. (color online) The ratio of the real to imaginary parts of the forward scattering amplitude
ρ in thepp andˉpp elastic collisions as a function of the center-of-mass energy√s (in GeV) given by the FPO model. Measurements by TOTEM in the whole energy range explored by the LHC [1–11] are also shown.As can be seen from Fig. 4, there is a good agreement with all experimental data [1–11], including the new data by TOTEM for
σpptot at√s = 2.76, 7, 8 and 13 TeV [4–11]. However, the ATLAS and cosmic data are incompatible with the TOTEM data and our theoretical predictions. The ATLAS measurement forσpptot at√s = 8 TeV is (96.07±0.92) mb, but the new TOTEM measurement forσpptot at√s = 8 TeV is (102.9±2.3) mb and (101.5±2.1) mb. Our theoretical predictions are consistent with the new TOTEM data. In Table 2, we show all TOTEM data compared with the FPO predictions.√s /TeV

σpptot/mb 

σpptot/mb 

ρpp 

ρpp 

TOTEM FPO TOTEM FPO 2.76 84.7±3.3 85.4 − − 7 98.6±2.2 99.7 − − 98.0±2.5 8 101.5±2.3 101.9 0.12±0.3 

0.121 

102.9±2.1 13 110.6±3.4 109.9 0.098±0.01 

0.110 Table 2. TOTEM measurements for
σtot andρ and the results of the FPO model.We show in Fig. 5 the ratio of the real to imaginary parts of the forward scattering amplitude
ρ as a function of the center-of-mass energy√s . The theoretical curve from the FPO model is also given in Fig. 5. One can see a good agreement between the TOTEM measurement ofρpp (0.12±0.3) at√s = 8 TeV and our prediction. However, the TOTEM value ofρpp (0.098±0.01) at√s = 13 TeV is smaller than our theoretical prediction. -
In Ref. [31], the Reggeon-Pomeron exchange model is proposed to describe the proton- antiproton elastic scattering
Fpp(s,t)=FR(s,t)+FP(s,t).

(43) The total cross-section in the Reggeon-Pomeron model is the sum of two terms:
σtot=XsαR(0)−1+YsαP(0)−1,

(44) where the Pomeron intercept
αP(0)=1.08 and the Reggeon interceptαR(0)=0.5 fit the experimental data perfectly in the region of center-of-mass energy5.3GeV⩽√s⩽2TeV .The total cross-section of the pp and
ˉpp elastic collisions in our FPO model is given by the sum of four parts:σppˉpp(tot)=σH+CsαP(0)−1+DsαR(0)−1±EsαO(0)−1.

(45) We expect a value of the Odderon intercept of about 0.5 in the fit. It is interesting that the Odderon intercept is much smaller than the Pomeron intercept.
Various calculations were performed of the Odderon intercept. The Bartels Kwieci
ˊn ski Praszalowicz (BKP) equation [32, 33] is known to give an excellent description of the Odderon in perturbative QCD. The Odderon singularity is the solution of the BKP equation for three color symmetric gluons. The Odderon interceptαO is calculated by the variational method asαO(0)=1+ωBKP(0)=1+Ncαsπ32ε3,

(46) where
Nc=3 , andαs=0.2 is the QCD coupling constant.The BKP equation has two explicit solutions. The intercept
αO of the BLC Odderon solution [34] is equal to 1,αO(0)=1,

(47) while the JW solution [35] gives the Odderon intercept as
αO(0)=0.96.

(48) Let us assume that the Odderon intercept in our FPO model is the solution of the BKP equation. Our result is compatible with
−32ε3=−2.625 , which is a supercritical Odderon, so that the Odderon intercept isαO=0.5 .We compare our result to other calculations in Table 3. A number of possible solutions were found in [34–43]. Different schemes of variational calculation were proposed, so that the corresponding Odderon intercepts are also different. As can be seen from Table 3, the Odderon intercept lies in the interval
1−(Ncαs/π)2.625⩽αO(0)⩽ 1+(Ncαs/π)4.16 .Table 3. Comparison of our result with other calculations of the Odderon intercept.
-
We propose a new approach to investigate the phenomenological Odderon based on the crossing symmetry, the Froissart-Martin theorem and the conventional Regge theory, which we call the Froissart Pomeron Odderon model (FPO).
We have calculated the total cross-section and the ratio of the real to imaginary parts of the forward scattering amplitude in the
pp andˉpp elastic collisions in the FPO model. With a smaller number of adjustable parameters than other models, the FPO model provides a fit to all existing experimental data for the high energypp andˉpp elastic collisions, including the new TOTEM data forσpptot at√s = 2.76, 7, 8 and 13 TeV, and the new TOTEM data forρ [4–11]. The results show that the Odderon, which includes the odd amplitudeF− , predicts the difference between thepp andˉpp elastic collisions.We assume an Odderon intercept
αO (0) = 0.5, which corresponds to the odd amplitudeF− in the Regge limit. Many models have studied the Odderon intercept [34–43], with the values of the intercept of exactly one or close to one. We also considered two cases in our model, a non-maximal Odderon with an intercept equal to 0.5 based on the fit results, and an Odderon which couples to external particles. We will continue to study the case of the maximal Odderon, and the Odderon intercept in general.The Odderon is identified as a triple-gluon exchange in
pp andˉpp scattering. The new TOTEM data forσtot andρ could be considered as an experimental proof of the Odderon. Our next goal is to extend the FPO model to the nuclear slope parameter [44] and the differential cross-sectiondσdt [45], and use the Odderon to explain the dip mechanism in the differential cross-sectiondσdt at high energies.
Possible Odderon exchange in pp and ˉpp elastic collisions at the TOTEM experiment
- Received Date: 2019-07-12
- Available Online: 2020-02-01
Abstract: Based on the Froissart-Martin theorem, the Regge theory and the possible Odderon exchange, the total cross-section






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF










































 DownLoad:
DownLoad: