THE SU2×SU2 BASIS AND THE PHYSICAL BASES FOR THE STATE VECTORS OF d-BOSON SYSTEMS AND THE TRACELESS BOSON OPERATORS (Ⅰ)
- Received Date: 1982-03-04
- Accepted Date: 1900-01-01
- Available Online: 1982-10-05
Abstract: The group chain U5![]() O5
O5![]() SU2×SU2 used by K. T. Hecht (1965) and by the othersprovides an important representation for expressing the physical basis of d-boson sys-tems. However the methods which have been introduced for this SU2×SU2 representa-tion to construct a physical basis is poorer in comparison with those for the otherrepresentations. In view of this we try to find appropriate methods to obtain the SU2×SU2 representation wave functions of the existing physical bases constructed byChacon et al. and by Szpikowski et al., In the present paper we analyse the SU2×SU2 tensor properties of the,bosonoperators and Vilenkin's traceless boson operators and express succinctly the elementaryvectors of the SU2×SU2 basis, the |PP SU2×SU2 > vectors, in terms of the tracelessoperators. With the help of this form of the| PP SU2 SU2> vectors we derive a simpleformula for obtaining the SU2×SU2 -representation wave functions of a physical basisfrom its (nμ)-representation wave functions. Thus the problem mentioned above is partlysolved. The other parts of the solution of the problem will be found in a coming paper.
SU2×SU2 used by K. T. Hecht (1965) and by the othersprovides an important representation for expressing the physical basis of d-boson sys-tems. However the methods which have been introduced for this SU2×SU2 representa-tion to construct a physical basis is poorer in comparison with those for the otherrepresentations. In view of this we try to find appropriate methods to obtain the SU2×SU2 representation wave functions of the existing physical bases constructed byChacon et al. and by Szpikowski et al., In the present paper we analyse the SU2×SU2 tensor properties of the,bosonoperators and Vilenkin's traceless boson operators and express succinctly the elementaryvectors of the SU2×SU2 basis, the |PP SU2×SU2 > vectors, in terms of the tracelessoperators. With the help of this form of the| PP SU2 SU2> vectors we derive a simpleformula for obtaining the SU2×SU2 -representation wave functions of a physical basisfrom its (nμ)-representation wave functions. Thus the problem mentioned above is partlysolved. The other parts of the solution of the problem will be found in a coming paper.


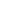
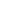
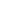
 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: