-
Since the discovery of
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons produced in electron-positron collisions [1−3], the three mesons have been of interest to hadron physicists [4−10]. They are easily produced at electron-positron colliders. Via electromagnetic interactions, the electron and positron become a virtual photon that splits into a charm quark and charm antiquark. This colorless$ c\bar c $ pair of a small size evolves into a$ c\bar c $ meson directly if the$ c\bar c $ relative momentum is small or indirectly by radiating gluons if the relative momentum is large. The production of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ in$ e^+ e^- $ annihilation can be studied in nonrelativistic quantum chromodynamics (QCD) that includes color-singlet and color-octet contributions [11] or from an electron-positron-photon vertex, a photon propagator, and the direct connection between the photon and the$ \psi (4040) $ and$ \psi (4160) $ meson fields [12, 13].Further interest in
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons has arisen in the context of ultrarelativistic heavy-ion collisions. The history of ultrarelativistic heavy-ion collisions is divided into the following stages: initial nucleus-nucleus collisions, thermalization of deconfined quark-gluon matter that has no temperatures, evolution of quark-gluon plasmas, hadronization of the quark-gluon plasma at the critical temperature$ T_{\rm{c}} $ , and evolution of hadronic matter until kinetic freeze-out. Some species of hadrons produced in Pb-Pb collisions at the Large Hadron Collider (LHC) have been measured. We expect the production of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons in Pb-Pb collisions within QCD.$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons are generally identified with the$ 3 ^3S_1 $ ,$ 2 ^3D_1 $ , and$ 4 ^3S_1 $ states of a charm quark and charm antiquark, respectively [14−17]. Because$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons are dissolved in hadronic matter when the temperature of hadronic matter is larger than$ 0.97T_{\rm{c}} $ ,$ 0.95T_{\rm{c}} $ , and$ 0.87T_{\rm{c}} $ , respectively [18], they can only be produced in hadronic matter. An open-charm meson contains only a charm quark or charm antiquark. Quark interchange between two open-charm mesons in association with color interactions between two constituents may produce charmonia. Therefore, the production of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ can be used to probe hadronic matter that results from the quark-gluon plasma created in ultrarelativistic heavy-ion collisions [18].The production of
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons in$ e^+ e^- $ annihilation relates to electromagnetic and strong interactions, whereas the one in ultrarelativistic heavy-ion collisions invloves only strong interactions. The mechanism of the latter is different from that of the former. Models differ according to the corresponding mechanisms.Hadronic matter contains not only charmed mesons (for example,
$ D^+ $ ,$ D^- $ ,$ D^0 $ ,$ \bar{D}^0 $ ,$ D^{*+} $ ,$ D^{*-} $ ,$ D^{*0} $ , and$ \bar{D}^{*0} $ mesons) but also charmed strange mesons (for example,$ D_s^+ $ ,$ D_s^- $ ,$ D_s^{*+} $ , and$ D_s^{*-} $ mesons). In this work, we study the production of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ via quark interchange between a charmed meson and charmed strange meson and between two charmed strange mesons in hadronic matter. This includes establishing master rate equations with new source terms that involve charmed strange mesons, calculating cross sections for the production of the charmonia in meson scattering by charmed strange mesons, and studying the number densities of the charmonia yielded in central Pb-Pb collisions at the center-of-mass energy per nucleon-nucleon pair$\sqrt{s_{_{NN}}}=5.02$ TeV at the LHC. We note that the charmonium production in the scattering of charmed strange mesons by open-charm mesons has not been studied.In a vacuum,
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons decay to two open-charm mesons, where the masses of the three charmonia are larger than the sum of the masses of the two open-charm mesons. The Schrödinger equation with the potential that will be presented in Sec. III yields energy eigenvalues and quark-antiquark relative-motion wave functions. The sum of an eigenvalue, the quark mass, and the antiquark mass produces a meson mass. The potential originates from perturbative QCD at short distances and lattice QCD at intermediate and large distances. The confining potential that corresponds to the lattice results depends on temperature, and its value becomes increasingly smaller with increasing temperature. It contributes to the eigenvalues and meson masses. Corresponding to meson quantum numbers, the Schrödinger equation indicates that the quark-antiquark relative-motion wave functions of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ occupy a large space and those of D,$ D^* $ ,$ D_s $ , and$ D_s^* $ occupy a small space at zero temperature. Hence,$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons are more sensitive to confinement than D,$ D^* $ ,$ D_s $ , and$ D_s^* $ mesons. When the temperature increases from zero, confinement becomes weaker, and confinement contributions to$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ masses decrease faster than contributions to D,$ D^* $ ,$ D_s $ , and$ D_s^* $ masses. In hadronic matter, the masses of the three charmonia become smaller than the sum of the masses of the two open-charm mesons [18]. Thus, the charmonium decays to the two open-charm mesons are forbidden by energy conservation. Hence,$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons are stable in hadronic matter.The remainder of this paper is organized as follows. In Sec. II, we establish master rate equations for
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons. In Sec. III, we provide the cross-section formulas for the inelastic meson-meson scattering governed by quark interchange and introduce the temperature-dependent interquark potential. In Sec. IV, we present numerical cross sections for twenty-seven reactions, show number densities of the three mesons produced in central Pb-Pb collisions, and provide relevant discussions. In Sec. V, we summarize this paper. -
We use the notation
$ D=\left(\begin{array}{c}D^+\\ D^0 \end{array} \right) $ ,$ \bar{D}=\left(\begin{array}{c}\bar{D}^0\\ D^- \end{array} \right) $ ,$ K=\left( \begin{array}{c}K^+\\ K^0 \end{array} \right) $ ,$ \bar{K}=\left( \begin{array}{c}\bar{K}^0\\ K^- \end{array} \right) $ ,$ D^{\ast}=\left( \begin{array}{c}D^{\ast +}\\ D^{\ast 0} \end{array} \right) $ ,$ \bar{D}^{\ast}=\left( \begin{array}{c}\bar{D}^{\ast 0}\\ D^{\ast -} \end{array} \right) $ ,$ K^{\ast}=\left(\begin{array}{c}K^{\ast +}\\ K^{\ast 0} \end{array} \right) $ , and$ \bar{K}^{\ast}=\left(\begin{array}{c}\bar{K}^{\ast 0}\\ K^{\ast -} \end{array} \right) $ for the isospin doublets. Hadronic matter produced in Pb-Pb collisions at LHC energies contains many charmed mesons and charmed strange mesons. The production of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons from two charmed mesons has been studied in Ref. [19]. Now we consider the production of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ from a charmed strange meson and charmed meson and from two charmed strange mesons as follows:$ D_s^+ \bar{D} \to K^\ast \psi(4040),\; D_s^+ \bar{D} \to K^\ast \psi(4160), \; D_s^+ \bar{D} \to K^\ast \psi(4415), $

$ D_s^+ \bar{D}^\ast \to K \psi(4040),\; D_s^+ \bar{D}^\ast \to K \psi(4160), \; D_s^+ \bar{D}^\ast \to K \psi(4415), $

$ D_s^+ \bar{D}^\ast \to K^\ast \psi(4040), \; D_s^+ \bar{D}^\ast \to K^\ast \psi(4160), \; D_s^+ \bar{D}^\ast \to K^\ast \psi(4415), $

$ D_s^{\ast +} \bar{D} \to K \psi(4040),\; D_s^{\ast +} \bar{D} \to K \psi(4160), \; D_s^{\ast +} \bar{D} \to K \psi(4415), $

$ D_s^{\ast +} \bar{D} \to K^\ast \psi(4040), \; D_s^{\ast +} \bar{D} \to K^\ast \psi(4160), \; D_s^{\ast +} \bar{D} \to K^\ast \psi(4415), $

$ D_s^{\ast +} \bar{D}^\ast \to K \psi(4040), \; D_s^{\ast +} \bar{D}^\ast \to K \psi(4160), \; D_s^{\ast +} \bar{D}^\ast \to K \psi(4415), $

$ D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4040), \; D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4160), \; D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4415), $

$ D_s^+ D_s^{\ast -} \to \eta \psi(4040),\; D_s^+ D_s^{\ast -} \to \eta \psi(4160), \; D_s^+ D_s^{\ast -} \to \eta \psi(4415), $

$ D_s^{\ast +} D_s^{\ast -} \to \eta \psi(4040), \; D_s^{\ast +} D_s^{\ast -} \to \eta \psi(4160), \; D_s^{\ast +} D_s^{\ast -} \to \eta \psi(4415). $

Applying charge conjugation to the above reactions, we obtain
$ D_s^- D $ ,$ D_s^- D^\ast $ ,$ D_s^{\ast -} D $ ,$ D_s^{\ast -} D^\ast $ , and$ D_s^- D_s^{\ast +} $ reactions. In total, in this study, we consider fifty-one new reactions to produce$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons.We denote the number densities of
$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons by$ n_{\psi (4040)} $ ,$ n_{\psi (4160)} $ , and$ n_{\psi (4415)} $ , respectively. These number densities change according to the following rate equation:$ \begin{aligned} \partial_{\mu}(n_{R}u^{\mu})=\varTheta_{R}, \end{aligned} $

(1) where μ is the space-time index, R represents
$ \psi (4040) $ ,$ \psi (4160) $ , or$ \psi (4415) $ , and$ u^{\mu} $ is the four-velocity of a fluid element in hadronic matter. We use$ v_{ij} $ for the relative velocity of mesons i and j and$ \sigma_{ij \to i^\prime j^\prime} $ for the isospin-averaged unpolarized cross section of$ ij \to i^\prime j^\prime $ . The source terms are given by$ \begin{aligned}[b] \varTheta_R= \;&\langle\sigma_{D\bar{D} \rightarrow \rho R}v_{D\bar D}\rangle n_Dn_{\bar D} +\langle\sigma_{D\bar{D}^* \rightarrow \pi R}v_{D\bar{D}^*}\rangle n_D n_{\bar{D}^*} +\langle\sigma_{D^*\bar{D} \rightarrow \pi R}v_{D^*\bar D}\rangle n_{D^*} n_{\bar D} +\langle\sigma_{D\bar{D}^* \rightarrow \rho R}v_{D\bar{D}^*}\rangle n_D n_{\bar{D}^*} \\ &+\langle\sigma_{D^*\bar{D} \rightarrow \rho R}v_{D^*\bar D}\rangle n_{D^*} n_{\bar D} +\langle\sigma_{D^*\bar{D}^* \rightarrow \pi R}v_{D^*\bar{D}^*}\rangle n_{D^*} n_{\bar{D}^*} +\langle\sigma_{D^*\bar{D}^* \rightarrow \rho R}v_{D^*\bar{D}^*}\rangle n_{D^*}n_{\bar{D}^*} +\langle\sigma_{D_s^+\bar{D} \rightarrow K^* R}v_{D_s^+\bar D}\rangle n_{D_s^+}n_{\bar D} \\ &+\langle\sigma_{D_s^-D \rightarrow \bar{K}^* R}v_{D_s^-D}\rangle n_{D_s^-}n_D +\langle\sigma_{D_s^+\bar{D}^* \rightarrow K R}v_{D_s^+\bar{D}^*}\rangle n_{D_s^+}n_{\bar{D}^*} +\langle\sigma_{D_s^-D^* \rightarrow \bar{K} R}v_{D_s^-D^*}\rangle n_{D_s^-}n_{D^*} +\langle\sigma_{D_s^+\bar{D}^* \rightarrow K^* R}v_{D_s^+\bar{D}^*}\rangle n_{D_s^+}n_{\bar{D}^*} \\ &+\langle\sigma_{D_s^-D^* \rightarrow \bar{K}^* R}v_{D_s^-D^*}\rangle n_{D_s^-}n_{D^*} +\langle\sigma_{D_s^{*+}\bar{D} \rightarrow K R}v_{D_s^{*+}\bar D}\rangle n_{D_s^{*+}}n_{\bar D} +\langle\sigma_{D_s^{*-}D \rightarrow \bar{K} R}v_{D_s^{*-}D}\rangle n_{D_s^{*-}}n_D +\langle\sigma_{D_s^{*+}\bar{D} \rightarrow K^* R}v_{D_s^{*+}\bar D}\rangle n_{D_s^{*+}}n_{\bar D} \\ &+\langle\sigma_{D_s^{*-}D \rightarrow \bar{K}^* R}v_{D_s^{*-}D}\rangle n_{D_s^{*-}}n_D +\langle\sigma_{D_s^{*+}\bar{D}^* \rightarrow K R}v_{D_s^{*+}\bar{D}^*}\rangle n_{D_s^{*+}}n_{\bar{D}^*} +\langle\sigma_{D_s^{*-}D^* \rightarrow \bar{K} R}v_{D_s^{*-}D^*}\rangle n_{D_s^{*-}}n_{D^*} +\langle\sigma_{D_s^{*+}\bar{D}^* \rightarrow K^* R}v_{D_s^{*+}\bar{D}^*} \rangle n_{D_s^{*+}}n_{\bar{D}^*} \\ &+\langle\sigma_{D_s^{*-}D^* \rightarrow \bar{K}^* R}v_{D_s^{*-}D^*}\rangle n_{D_s^{*-}}n_{D^*} +\langle\sigma_{D_s^+D_s^{*-} \rightarrow \eta R}v_{D_s^+D_s^{*-}}\rangle n_{D_s^+}n_{D_s^{*-}} +\langle\sigma_{D_s^{*+}D_s^- \rightarrow \eta R}v_{D_s^{*+}D_s^-}\rangle n_{D_s^{*+}}n_{D_s^-} +\langle\sigma_{D_s^{*+}D_s^{*-} \rightarrow \eta R}v_{D_s^{*+}D_s^{*-}}\rangle n_{D_s^{*+}}n_{D_s^{*-}} \\ &-\langle\sigma_{\rho R \rightarrow D\bar{D}}v_{\rho R}\rangle n_\rho n_R -\langle\sigma_{\pi R \rightarrow D\bar{D}^*}v_{\pi R}\rangle n_\pi n_R -\langle\sigma_{\pi R \rightarrow D^*\bar{D}}v_{\pi R}\rangle n_\pi n_R -\langle\sigma_{\rho R \rightarrow D\bar{D}^*}v_{\rho R}\rangle n_\rho n_R \\ &-\langle\sigma_{\rho R \rightarrow D^*\bar{D}}v_{\rho R}\rangle n_\rho n_R -\langle\sigma_{\pi R \rightarrow D^*\bar{D}^*}v_{\pi R}\rangle n_\pi n_R -\langle\sigma_{\rho R \rightarrow D^*\bar{D}^*}v_{\rho R}\rangle n_\rho n_R -\langle\sigma_{K^* R \rightarrow D_s^+\bar{D}}v_{K^* R}\rangle n_{K^*} n_R \\ &-\langle\sigma_{\bar{K}^* R \rightarrow D_s^-D}v_{\bar{K}^* R}\rangle n_{\bar{K}^*} n_R -\langle\sigma_{K R \rightarrow D_s^+\bar{D}^*}v_{K R}\rangle n_K n_R -\langle\sigma_{\bar{K} R \rightarrow D_s^-D^*}v_{\bar{K} R}\rangle n_{\bar{K}} n_R -\langle\sigma_{K^* R \rightarrow D_s^+\bar{D}^*}v_{K^* R}\rangle n_{K^*}n_R \\ &-\langle\sigma_{\bar{K}^* R \rightarrow D_s^-D^*}v_{\bar{K}^* R}\rangle n_{\bar{K}^*} n_R -\langle\sigma_{K R \rightarrow D_s^{*+}\bar{D}}v_{K R}\rangle n_Kn_R -\langle\sigma_{\bar{K} R \rightarrow D_s^{*-}D}v_{\bar{K} R}\rangle n_{\bar{K}} n_R -\langle\sigma_{K^* R \rightarrow D_s^{*+}\bar{D}}v_{K^* R}\rangle n_{K^*}n_R \\ &-\langle\sigma_{\bar{K}^* R \rightarrow D_s^{*-}D}v_{\bar{K}^* R}\rangle n_{\bar{K}^*} n_R -\langle\sigma_{K R \rightarrow D_s^{*+}\bar{D}^*}v_{K R}\rangle n_K n_R -\langle\sigma_{\bar{K} R \rightarrow D_s^{*-}D^*}v_{\bar{K} R}\rangle n_{\bar{K}} n_R -\langle\sigma_{K^* R \rightarrow D_s^{*+}\bar{D}^*}v_{K^* R} \rangle n_{K^*} n_R \\ &-\langle\sigma_{\bar{K}^* R \rightarrow D_s^{*-}D^*}v_{\bar{K}^* R}\rangle n_{\bar{K}^*} n_R -\langle\sigma_{\eta R \rightarrow D_s^+D_s^{*-}}v_{\eta R}\rangle n_\eta n_R -\langle\sigma_{\eta R \rightarrow D_s^{*+}D_s^-}v_{\eta R}\rangle n_\eta n_R -\langle\sigma_{\eta R \rightarrow D_s^{*+}D_s^{*-}}v_{\eta R}\rangle n_\eta n_R , \end{aligned} $

(2) where
$ n_D $ ,$ n_{\bar D} $ ,$ n_{D^*} $ ,$ n_{\bar{D}^*} $ ,$ n_{D_s^+} $ ,$ n_{D_s^-} $ ,$ n_{D_s^{*+}} $ ,$ n_{D_s^{*-}} $ ,$ n_\pi $ ,$ n_\rho $ ,$ n_K $ ,$ n_{\bar K} $ ,$ n_{K^\ast} $ ,$ n_{\bar{K}^\ast} $ , and$ n_\eta $ are the number densities of D,$ \bar D $ ,$ D^* $ ,$ \bar{D}^* $ ,$ D_s^+ $ ,$ D_s^- $ ,$ D_s^{*+} $ ,$ D_s^{*-} $ , π, ρ, K,$ \bar K $ ,$ K^\ast $ ,$ \bar{K}^\ast $ , and η mesons, respectively;$ \langle \sigma_{ij\to i^\prime j^\prime} v_{ij}\rangle $ indicates the average cross section weighted by the relative velocity,$ \langle \sigma_{ij\to i^\prime j^\prime} v_{ij}\rangle =\frac{\int\dfrac{{\rm d}^3 k_i}{(2\pi)^3}f_i(k_i) \dfrac{{\rm d}^3 k_j}{(2\pi)^3}f_j(k_j)\sigma_{ij \to i^\prime j^\prime} (\sqrt{s}, T)v_{ij}} {\int\dfrac{{\rm d}^3 k_i}{(2\pi)^3}f_i(k_i)\int\dfrac{{\rm d}^3 k_j}{(2\pi)^3} f_j(k_j)}, $

(3) where
$ \sqrt s $ is the center-of-mass energy of mesons i and j, T is the temperature, and$ f_i(k_i) $ is the momentum distribution function of meson i with the four-momentum$ k_i $ in the rest frame of hadronic matter. The first seven terms on the right-hand side of Eq. (2) have been considered in Ref. [19]. While the first twenty-four terms produce$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons, the last twenty-four terms break them.The master rate equations involve the temperature and transverse velocity of hadronic matter, which are given by the relativistic hydrodynamic equation:
$ \begin{aligned} \partial_{\mu}T^{\mu\nu}=0, \end{aligned} $

(4) where
$ T^{\mu\nu} $ is the energy-momentum tensor [20],$ \begin{aligned}[b] T^{\mu\nu}=\;&(\epsilon+P)u^{\mu}u^{\nu}-Pg^{\mu\nu} +\eta [\nabla^\mu u^\nu +\nabla^\nu u^\mu\\& -\frac{2}{3} (g^{\mu \nu}-u^\mu u^\nu)\nabla \cdot u], \end{aligned} $

(5) where
$ \nabla^\mu =\partial^\mu -u^\mu u \cdot \partial $ ; ϵ, P,$ g^{\mu \nu} $ , and η are the energy density, pressure, metric, and shear viscosity, respectively.For a large volume of particles, if cross sections for particle-particle scattering are very large, the mean free path of particles is very short, and the particles form a perfect fluid [20, 21]. Thus, the first two terms on the right-hand side of Eq. (5) produce the hydrodynamic equation
$ \begin{aligned} \partial_{\mu}[(\epsilon+P)u^{\mu}u^{\nu}-Pg^{\mu\nu}]=0. \end{aligned} $

(6) If the cross sections are not very large, the matter that the particles form is not a perfect fluid. Therefore, viscosities such as the shear viscosity, which is proportional to the inverse of the cross sections, must be considered when studying matter evolution. The influence of the bulk viscosity may be neglected [22]. By including the shear viscosity in the energy-momentum tensor in Eq. (5), we establish Eq. (4) [20].
If matter is in thermal equilibrium, hydrodynamics can be applied to it. To establish thermal equilibrium, particles must frequently collide with each other. Because pions are the dominant hadron species in hadronic matter, we study collision cases of pions. The average transverse momenta of charged pions and charged kaons produced in central Pb-Pb collisions at
$\sqrt{s_{_{NN}}}=5.02$ TeV are 0.5682 GeV/c and 0.9177 GeV/c, respectively [23]. Thus, we consider pions with a momentum of 0.5682 GeV/c and kaons with a momentum of 0.9177 GeV/c.We denote the Mandelstam variable by
$ \sqrt{s_{\pi \pi}} $ , which equals the square of the sum of two pion four-momenta. If two pions move in opposite directions, they produce the maximum of$ \sqrt{s_{\pi \pi}} $ . If the two pions move in the same direction, they produce the minimum of$ \sqrt{s_{\pi \pi}} $ . The average of the maximum and minimum is 0.723 GeV. From the cross section formulas presented in Ref. [24], we obtain the cross sections for elastic$ \pi \pi $ scattering for$ I=2 $ ,$ I=1 $ , and$ I=0 $ at$ \sqrt{s_{\pi \pi}}=0.723 $ GeV as 8.5 mb, 260.3 mb, and 112.1 mb, respectively. The three values agree with the measured cross sections for I=2 [25−27] and the data derived from the measured phase shifts for$ I=1 $ [28−34] and$ I=0 $ [30−36]. Consequently, the isospin-averaged cross section for elastic$ \pi \pi $ scattering is$ \sigma_{\pi \pi}^{\rm{un}}=103.9 $ mb.If a pion and kaon move in opposite (identical) directions, they produce the maximum (minimum) of the Mandelstam variable
$ \sqrt{s_{\pi K}} $ , which is the square of the sum of the pion and kaon four-momenta. The average of the maximum and minimum is 1.127 GeV. We obtain cross sections for elastic$ \pi K $ scattering for$ I=3/2 $ and$ I=1/2 $ at$ \sqrt{s_{\pi K}}=1.127 $ GeV as 2.59 mb and 21.7 mb, respectively. The two values agree with the measured cross sections for$ I=3/2 $ [37, 38] and the data derived from the experimental phase shifts for$ I=1/2 $ [39−42]. Consequently, the isospin-averaged cross section for elastic$ \pi K $ scattering is$ \sigma_{\pi K}^{\rm{un}}=8.96 $ mb.We denote the number density of pions in hadronic matter by
$ n_\pi $ . The mean free path of pions due to elastic$ \pi \pi $ scattering is$ 1/(n_\pi \sigma_{\pi \pi}) $ . However, pions may also collide with kaons. To include$ \pi K $ collisions, the mean free path is taken as$ 1/[n_\pi (\sigma_{\pi \pi}^{\rm{un}} +\dfrac{n_K}{n_\pi}\sigma_{\pi K}^{\rm{un}})] $ , where$ n_K $ is the number density of kaons in hadronic matter. The contribution of kaons to the mean free path of pions is weighted by$ n_K/n_\pi $ . When hadronic matter is produced at the critical temperature, the π and K number densities are 0.243$ {\rm{fm}}^{-3} $ and 0.0915$ {\rm{fm}}^{-3} $ , respectively, and hadronic matter has a size of 20.1 fm along the Pb beam and a size of 34.3 fm in the direction perpendicular to the beam. The mean free path of pions is 0.384 fm. When a pion moves from the center of hadronic matter to the matter surface along or perpendicular to the beam, the collision number is 26.2 or 44.7. When hadronic matter expands, the collision number decreases. At kinetic freeze-out, the π and K number densities are 0.0539$ {\rm{fm}}^{-3} $ and 0.0203$ {\rm{fm}}^{-3} $ , respectively, and hadronic matter has a size of 38.45 fm along the Pb beam and 52.65 fm in the direction perpendicular to the beam. The mean free path of pions is 1.73 fm. When a pion moves from the center of hadronic matter to the matter surface along or perpendicular to the beam, the collision number is 11.1 or 15.2. With the four collision numbers, thermal equilibrium can be established, and we suggest using hydrodynamics in hadronic matter that is created in central Pb-Pb collisions at$\sqrt{s_{_{NN}}}=5.02$ TeV.The foundation of hydrodynamics has been related to the Klein-Gordon and Schrödinger equations in Refs. [43, 44]. First- and second-order conformal viscous hydrodynamics were derived from the exact solution of the Boltzmann equation in the relaxation time approximation with Gubser symmetry in Ref. [45]. These works aid us in understanding the application of hydrodynamics to hadronic matter.
-
For the twenty-seven reactions listed in Sec. II, we consider the meson-meson scattering in which a meson consists of the charm quark c and light antiquark
$ \bar{q}_{2} $ and another meson consists of the light quark$ q_1 $ and charm antiquark$ \bar c $ . When the two mesons collide, the interchange of the c quark and$ q_1 $ quark leads to the reaction$ c\bar{q}_2 + q_1\bar{c} \rightarrow q_1\bar{q}_2 + c\bar{c} $ . We denote the mass and four-momentum of meson i (i =$ c\bar{q}_2 $ ,$ q_1\bar{c} $ ,$ q_1\bar{q}_2 $ ,$ c\bar{c} $ ) by$ m_i $ and$ P_i=(E_i,\vec{P}_i) $ , respectively. The Mandelstam variable is$ s=(P_{c\bar{q}_2}+P_{q_1\bar{c}})^2 $ . The unpolarized cross section for$ c\bar{q}_2 + q_1\bar{c} \rightarrow q_1\bar{q}_2 + c\bar{c} $ is$ \begin{aligned} \sigma^{\rm{unpol}}(\sqrt {s},T) & = \frac {1}{(2J_{c\bar{q}_2}+1)(2J_{q_1\bar{c}}+1)} \frac{1}{64\pi s}\frac{|\vec{P}^{\prime }(\sqrt{s})|}{|\vec{P}(\sqrt{s})|} \\ & \int_{0}^{\pi }{\rm d}\theta \sum\limits_{J_{c\bar{q}_2z}J_{q_1\bar{c}z}J_{q_1\bar{q}_2z}J_{c\bar{c}z}} (\mid {\cal M}_{\rm{fi}}^{\rm{prior}} \mid^2 + \mid {\cal M}_{\rm{fi}}^{\rm{post}} \mid^2) \sin \theta , \end{aligned} $

(7) where
$ J_{c\bar{q}_2z} $ ($ J_{q_1\bar{c}z} $ ,$ J_{q_1\bar{q}_2z} $ ,$ J_{c\bar{c}z} $ ) denotes the magnetic projection quantum number of the total angular momentum$ J_{c\bar{q}_2} $ ($ J_{q_1\bar{c}} $ ,$ J_{q_1\bar{q}_2} $ ,$ J_{c\bar{c}} $ ) of meson$ c\bar{q}_2 $ ($ q_1\bar{c} $ ,$ q_1\bar{q}_2 $ ,$ c\bar{c} $ );$ \vec{P} $ equals$ \vec{P}_{c\bar{q}_2} $ , and$ \vec{P}^{'} $ equals$ \vec{P}_{q_1\bar{q}_2} $ ;$ \theta $ is the angle between$ \vec{P} $ and$ \vec{P}' $ .Quark interchange produces two forms in the Born-order meson-meson scattering, prior form, and post form [46, 47]. Scattering in the prior form means that gluon exchange occurs prior to quark interchange. The transition amplitude for scattering in the prior form is
$ \begin{aligned}[b] {\cal M}_{\rm{fi}}^{\rm{prior}} =\;&4\sqrt{E_{c\bar{q}_2} E_{q_1\bar{c}} E_{q_1\bar{q}_2} E_{c\bar{c}}} \langle\psi_{q_1\bar{q}_2} \mid \langle\psi_{c\bar{c}} \mid \\&\times(V_{c\bar{c}}+V_{\bar{q}_2q_1}+V_{cq_1}+V_{\bar{q}_2\bar{c}} ) \mid \psi_{c\bar{q}_2}\rangle \mid \psi_{q_1\bar{c}}\rangle, \end{aligned} $

(8) where
$ \psi_{c\bar{q}_2} $ ($ \psi_{q_1\bar{c}} $ ,$ \psi_{q_1\bar{q}_2} $ ,$ \psi_{c\bar{c}} $ ) is the wave function of meson$ c\bar{q}_2 $ ($ q_1\bar{c} $ ,$ q_1\bar{q}_2 $ ,$ c\bar{c} $ ) and is the product of the color, spin, flavor, and mesonic quark-antiquark relative-motion wave functions;$ V_{ab} $ is the potential between constituents a and b. Scattering in the post form means that quark interchange is followed by gluon exchange. The transition amplitude for scattering in the post form is$ \begin{aligned}[b] {\cal M}_{\rm{fi}}^{\rm{post}} =\;&4\sqrt{E_{c\bar{q}_2} E_{q_1\bar{c}} E_{q_1\bar{q}_2} E_{c\bar{c}}} \langle\psi_{q_1\bar{q}_2} \mid \langle\psi_{c\bar{c}} \mid \\&\times(V_{q_1\bar{c}}+V_{\bar{q}_2c}+V_{cq_1}+V_{\bar{q}_2\bar{c}}) \mid \psi_{c\bar{q}_2}\rangle \mid \psi_{q_1\bar{c}}\rangle. \end{aligned} $

(9) Both
$ {\cal M}_{\rm{fi}}^{\rm{prior}} $ and$ {\cal M}_{\rm{fi}}^{\rm{post}} $ contain$ V_{cq_1} $ and$ V_{\bar{q}_2\bar{c}} $ . However,$\langle \psi_{q_1\bar{q}_2} \mid \langle \psi_{c\bar{c}} \mid (V_{c\bar{c}}+V_{\bar{q}_2q_1}) \mid \psi_{c\bar{q}_2} \rangle \mid \psi_{q_1\bar{c}}\rangle$ in$ {\cal M}_{\rm{fi}}^{\rm{prior}} $ may not to the same as$\langle \psi_{q_1\bar{q}_2} \mid \langle\psi_{c\bar{c}} \mid (V_{q_1\bar{c}}+ V_{\bar{q}_2c}) \mid \psi_{c\bar{q}_2} \rangle \mid \psi_{q_1\bar{c}}\rangle$ in$ {\cal M}_{\rm{fi}}^{\rm{post}} $ . Hence,$ {\cal M}_{\rm{fi}}^{\rm{post}} $ may not be equal to$ {\cal M}_{\rm{fi}}^{\rm{prior}} $ , which is the so-called post-prior discrepancy [48−50].The transition amplitudes result from interactions between all constituent pairs in different mesons. In this work, we consider a central spin-independent potential, spin-spin interaction, and tensor interaction. Derived from perturbative QCD and lattice gauge calculations [51−53], the potential for
$ T<T_{\rm{c}} $ is$ \begin{aligned}[b] V_{ab}(\vec{r}_{ab}) =\;& - \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \xi_1 \left[ 1.3- \left( \frac {T}{T_{\rm{c}}} \right)^4 \right] \tanh (\xi_2 r_{ab}) \\&+ \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {6\pi}{25} \frac {v(\lambda r_{ab})}{r_{ab}} \exp (-\xi_3 r_{ab}) \\ & -\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {16\pi^2}{25}\frac{{\rm d}^3}{\pi^{3/2}}\exp(-{\rm d}^2r^2_{ab}) \frac {\vec {s}_a \cdot \vec {s}_b} {m_am_b}\\& +\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2}\frac {4\pi}{25} \frac {1} {r_{ab}} \frac {{\rm d}^2v(\lambda r_{ab})}{{\rm d}r_{ab}^2} \frac {\vec {s}_a \cdot \vec {s}_b}{m_am_b} \\ & -\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {6\pi}{25m_am_b}\Bigg[ v(\lambda r_{ab}) -r_{ab}\frac {{\rm d}v(\lambda r_{ab})}{{\rm d}r_{ab}} \\&+\frac{r_{ab}^2}{3} \frac {{\rm d}^2v(\lambda r_{ab})}{{\rm d}r_{ab}^2} \Bigg] \left( \frac{3\vec {s}_a \cdot \vec{r}_{ab}\vec {s}_b \cdot \vec{r}_{ab}} {r_{ab}^5} -\frac {\vec {s}_a \cdot \vec {s}_b}{r_{ab}^3} \right) , \end{aligned} $

(10) where
$ \vec{r}_{ab} $ is the relative coordinate of constituents a and b;$ m_a $ ,$ \vec{s}_a $ , and$ \vec{\lambda}_a $ are the mass, spin, and Gell-Mann matrices for the color generators of constituent a, respectively;$ \xi_1=0.525 $ GeV,$ \xi_2=1.5[0.75+ 0.25 (T/{T_{\rm{c}}})^{10}]^6 $ GeV,$ \xi_3=0.6 $ GeV,$ T_{\rm{c}}=0.175 $ GeV, and$ \lambda=\sqrt{25/16\pi^2 \alpha'} $ with$ \alpha'=1.04 $ GeV$ ^{-2} $ ; the function v is given by Buchmüller and Tye [51]; the quantity d is related to constituent masses [19]. The constituent masses are 0.32 GeV, 0.32 GeV, 0.5 GeV, and 1.51 GeV for the up, down, strange, and charm quarks, respectively. The Schrödinger equation with$ V_{ab} (\vec{r}_{ab}) $ at zero temperature yields meson masses that are close to the experimental masses [54] of π, ρ, K,$ K^* $ , η,$ J/\psi $ ,$ \chi_{c} $ ,$ \psi' $ ,$ \psi (3770) $ ,$ \psi (4040) $ ,$ \psi (4160) $ ,$ \psi (4415) $ , D,$ D^* $ ,$ D_s $ , and$ D^*_s $ mesons. With the mesonic quark-antiquark relative-motion wave functions determined by the Schrödinger equation, the experimental data [25, 27−36, 55, 56] of S- and P-wave elastic phase shifts for$ \pi \pi $ scattering in a vacuum are reproduced in the Born approximation [57, 58].By including color screening in medium, the lattice gauge calculations [52] provide a numerical spin-independent and temperature-dependent potential at intermediate and large distances. The first and second terms on the right-hand side of Eq. (10) fit the numerical quark potential at
$ T>0.55T_{\rm{c}} $ well [59]. The expression$ \dfrac {\vec{\lambda}_a}{2} \cdot \dfrac {\vec{\lambda}_b}{2} \dfrac {6\pi}{25} \dfrac {v(\lambda r_{ab})}{r_{ab}} $ in the second term results from one-gluon exchange plus perturbative one- and two-loop corrections in a vacuum [51], and the factor$ \exp (-\xi_3 r_{ab}) $ is a medium modification factor. When the distance$ r_{ab} $ increases from zero, the numerical potential increases and becomes a distance-independent value at large distances at$ T>0.55T_{\rm{c}} $ . The value decreases with increasing temperature, which means that confinement becomes increasingly weaker. The value is parametrized as$ - \dfrac {\vec{\lambda}_a}{2} \cdot \dfrac {\vec{\lambda}_b}{2} \xi_1 \left[1.3- \left(\dfrac {T}{T_{\rm{c}}} \right)^4 \right] $ such that the first term isobtained. The function$ \tanh (\xi_2 r_{ab}) $ increases from 0 to 1 when$ r_{ab} $ increases from 0 to$ +\infty $ .$ \xi_2 $ increases when T increases. The larger the value of$ \xi_2 $ , the smaller the distance at which$ \tanh (\xi_2 r_{ab}) $ is nearly 1, i.e., the stronger the medium screening on the quark potential. The first term is the confining potential that corresponds to the lattice results. The third term is the smeared spin-spin interaction that results from one-gluon exchange between constituents a and b. The fourth term is the spin-spin interaction that originates from perturbative one- and two-loop corrections to one-gluon exchange. The fifth term is the tensor interaction that results from one-gluon exchange plus perturbative one- and two-loop corrections. -
We solve the Schrödinger equation with the potential given in Eq. (10) to obtain temperature-dependent meson masses and mesonic quark-antiquark relative-motion wave functions in coordinate space. The transition amplitudes in the prior and post forms are calculated from the Fourier transform of the potential and the wave functions. Temperature-dependent unpolarized cross sections are obtained from Eq. (7). The cross sections are plotted in Figs. 1−27 for the twenty-seven reactions listed in Sec. II. The cross sections for
$ D_s^- D $ ,$ D_s^- D^* $ ,$ D_s^{*-} D $ ,$ D_s^{*-} D^* $ , and$ D_s^- D_s^{*+} $ reactions are equal to those for$ D_s^+ \bar{D} $ ,$ D_s^+ \bar{D}^* $ ,$ D_s^{*+} \bar{D} $ ,$ D_s^{*+} \bar{D}^* $ , and$ D_s^+ D_s^{*-} $ reactions, respectively. These unpolarized cross sections lead to the isospin-averaged unpolarized cross sections in the source terms by a formula given in the appendix of Ref. [19].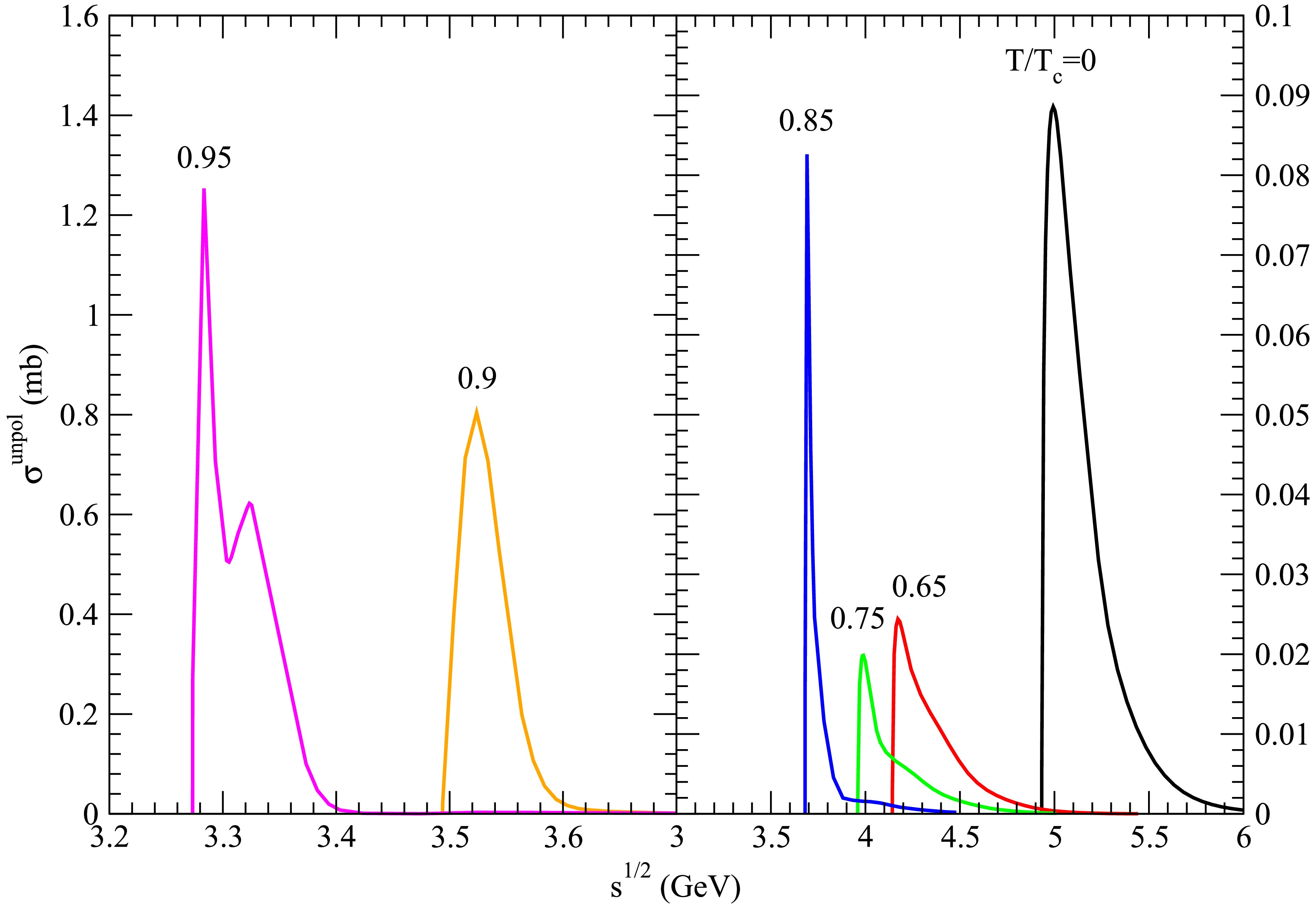
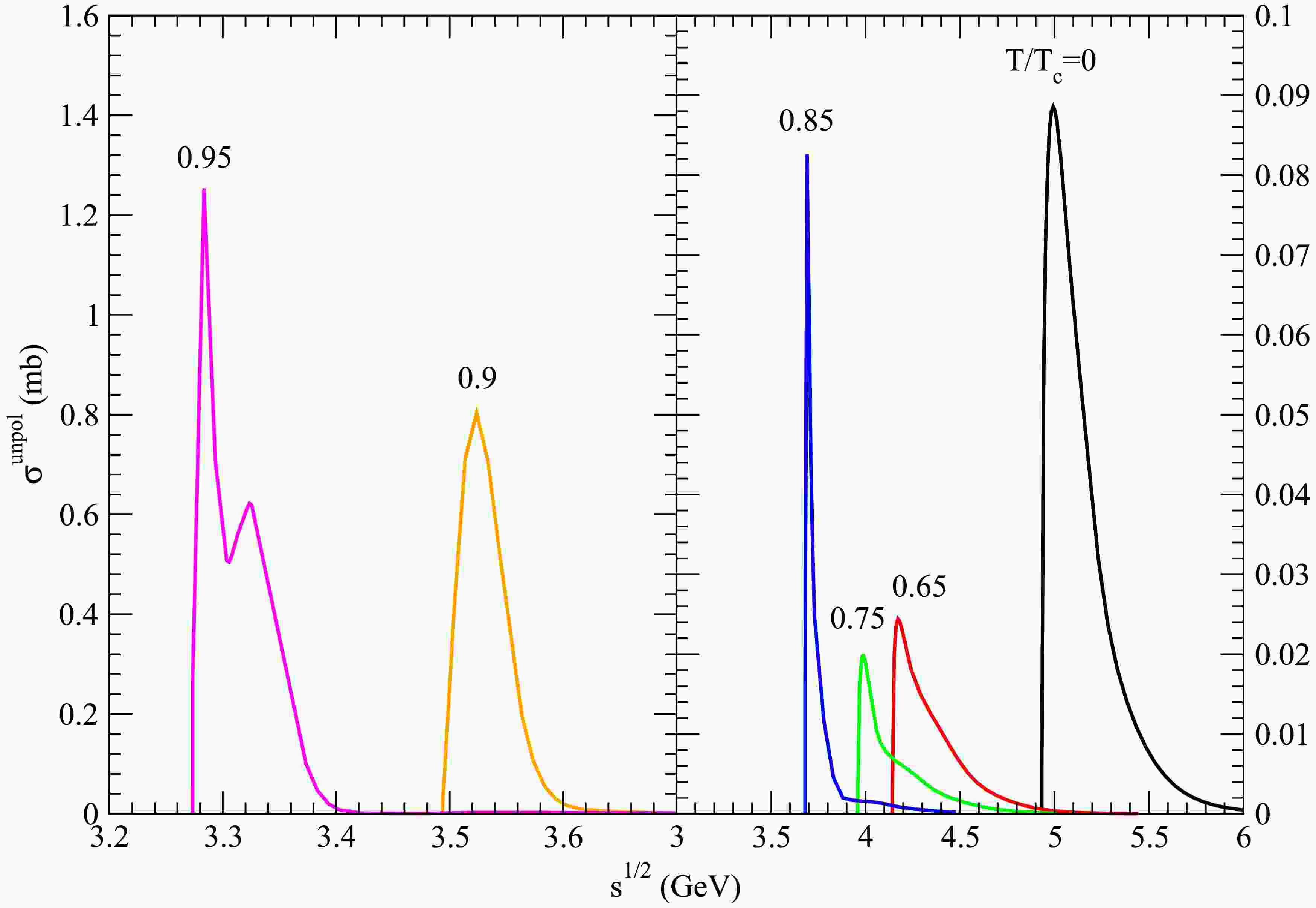
Figure 1. (color online) Cross sections for
$ D_s^+ \bar{D} \rightarrow K^\ast \psi(4040) $ at various temperatures.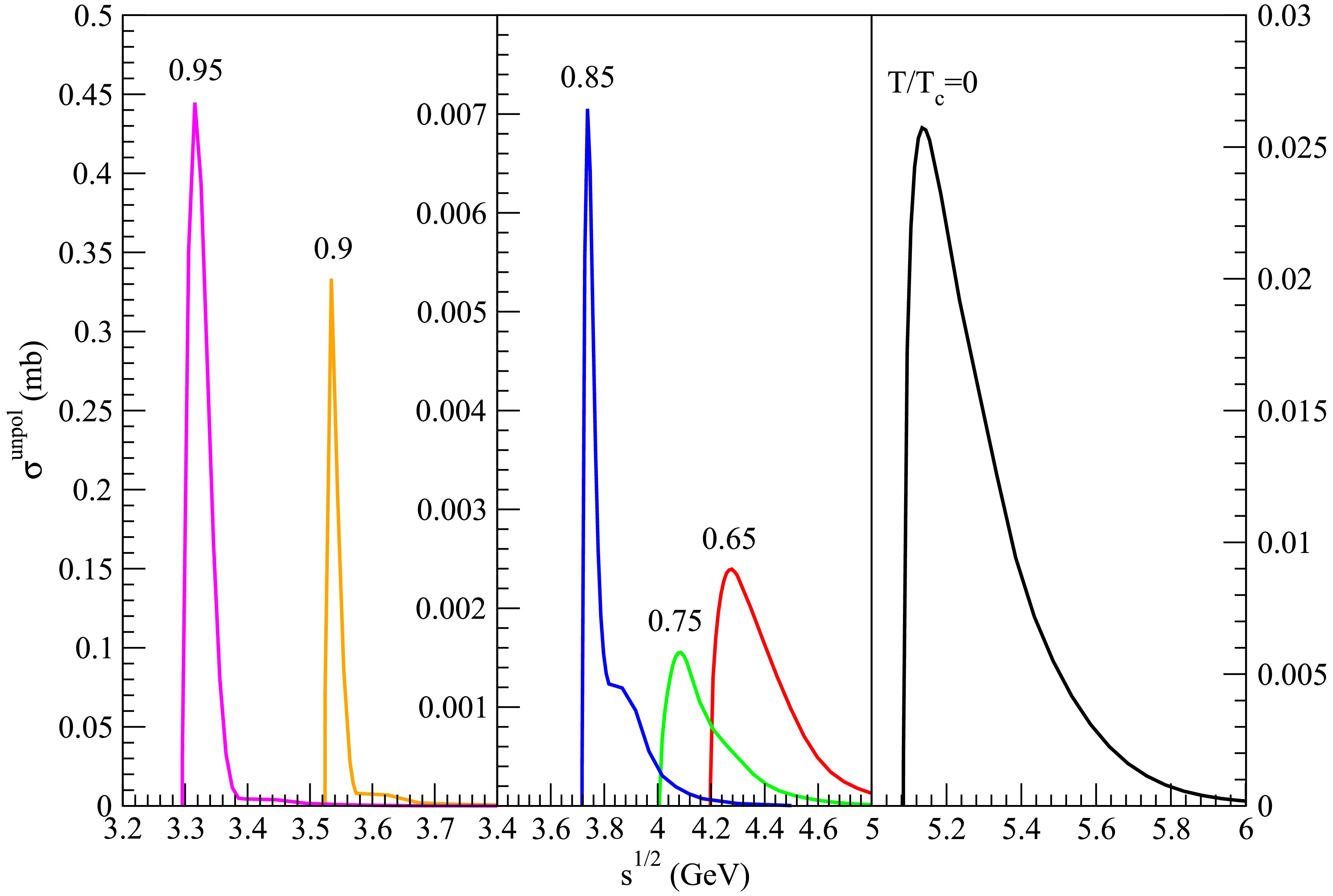
Figure 2. (color online) Cross sections for
$ D_s^+ \bar{D} \rightarrow K^\ast \psi(4160) $ at various temperatures.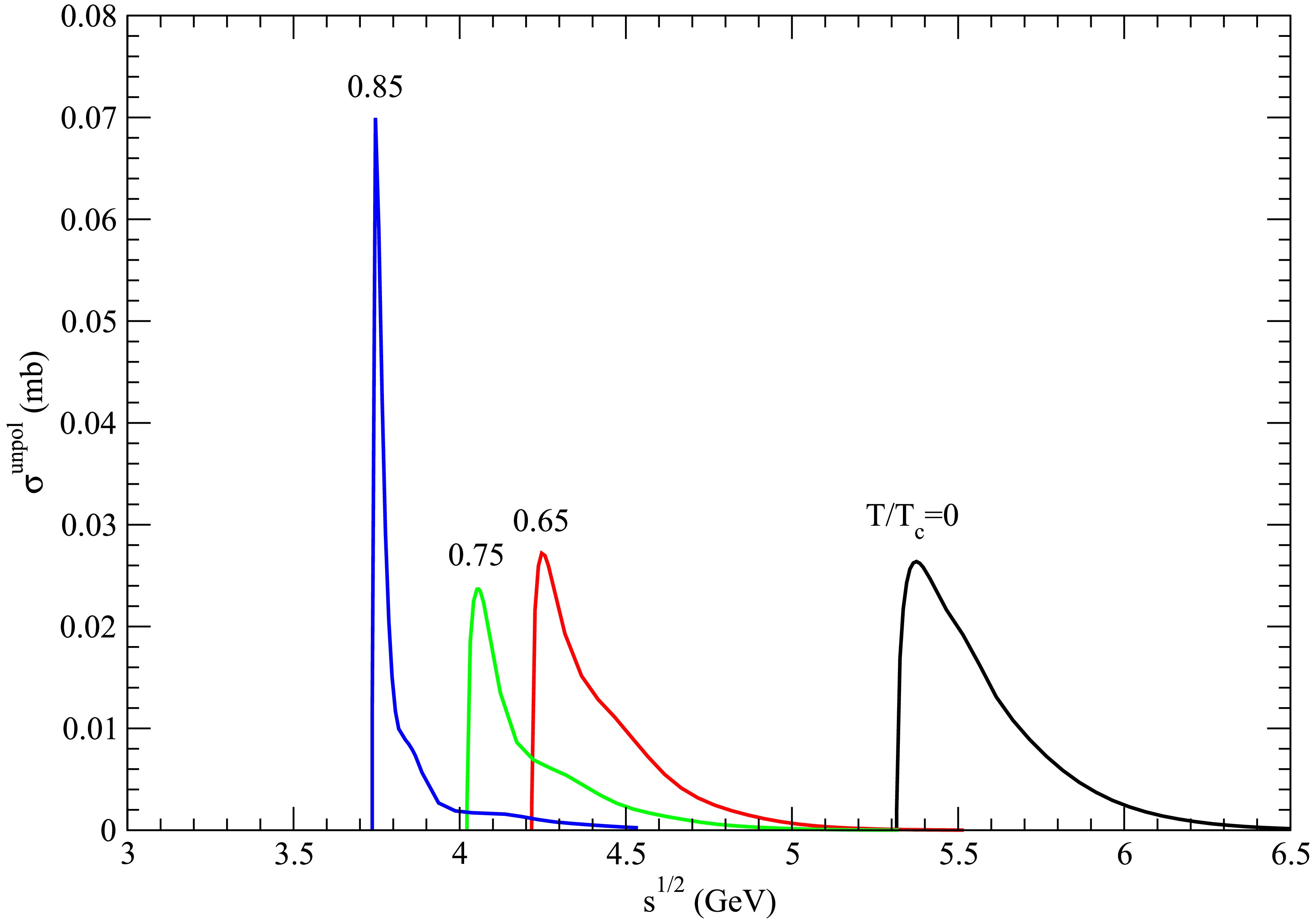
Figure 3. (color online) Cross sections for
$ D_s^+ \bar{D} \rightarrow K^\ast \psi(4415) $ at various temperatures.
Figure 4. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K \psi(4040) $ at various temperatures.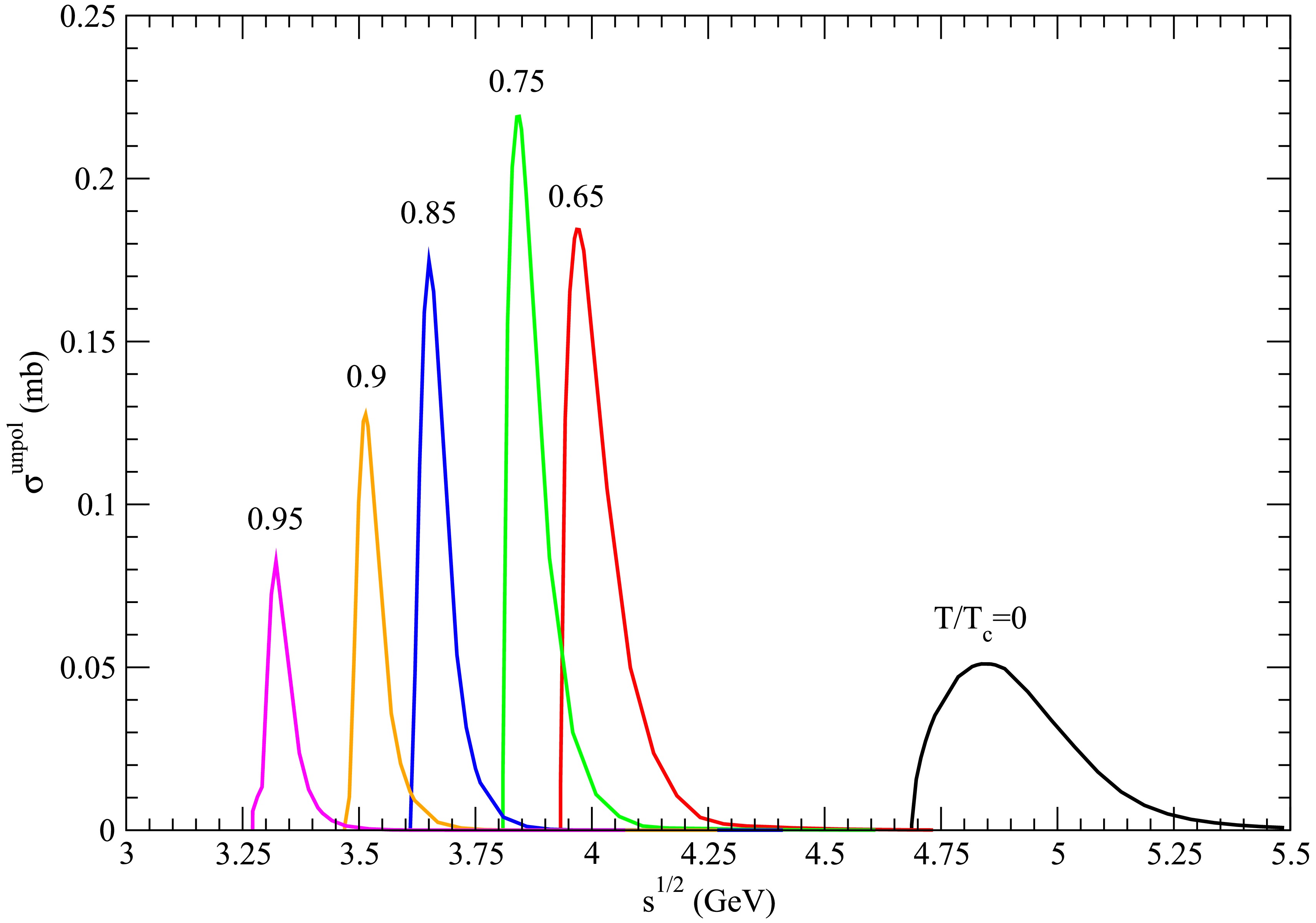
Figure 5. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K \psi(4160) $ at various temperatures.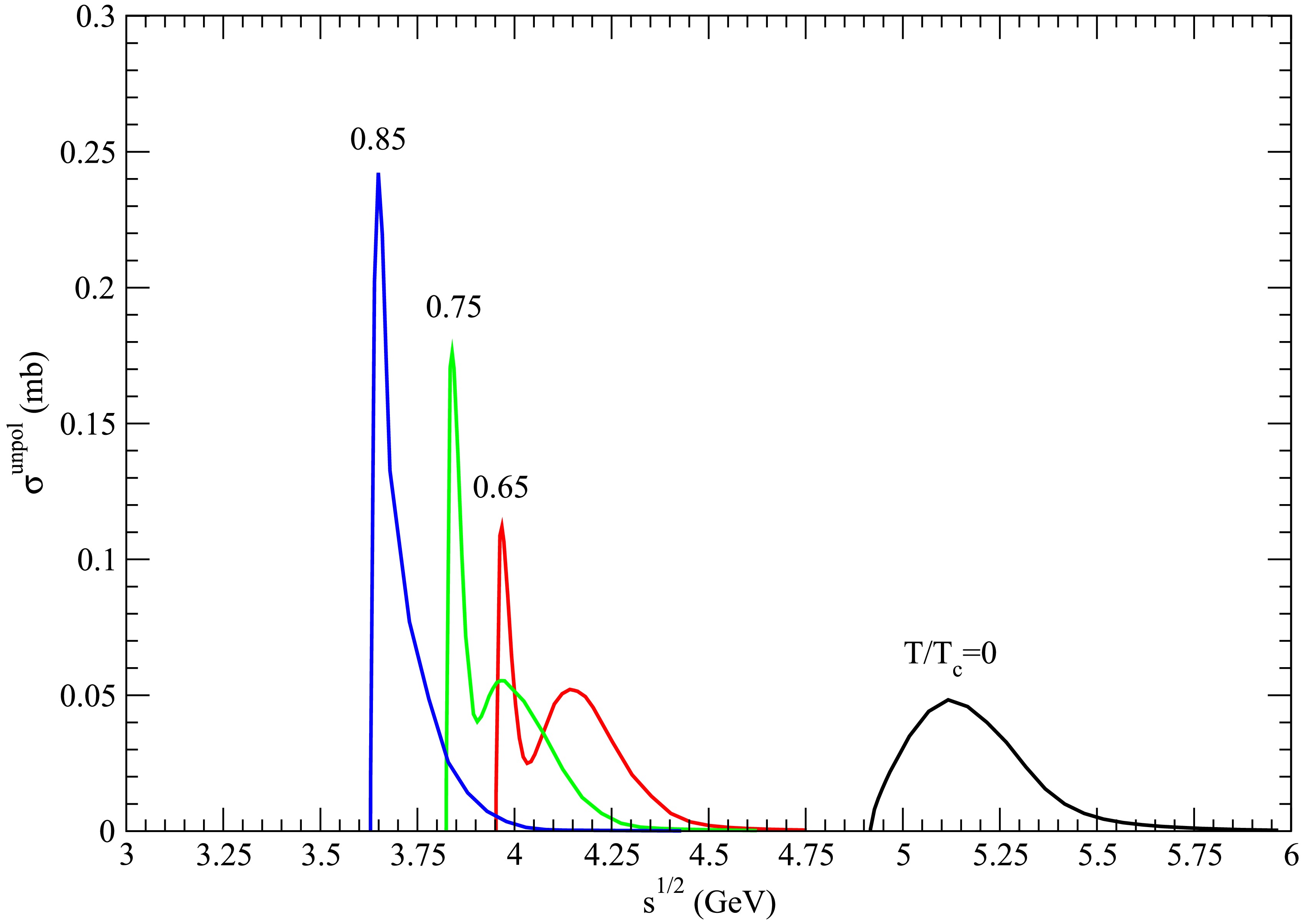
Figure 6. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K \psi(4415) $ at various temperatures.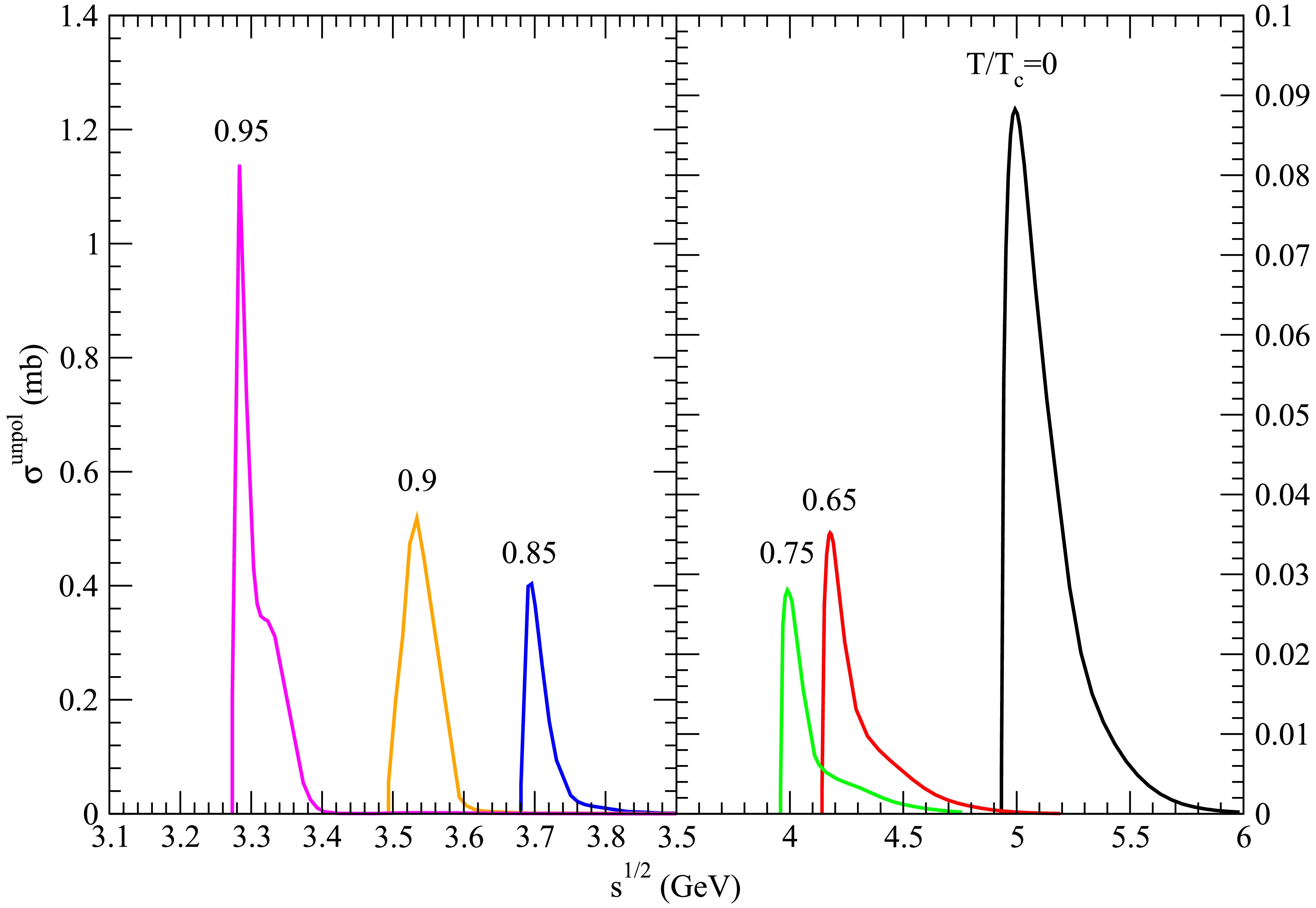
Figure 7. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K^\ast \psi(4040) $ at various temperatures.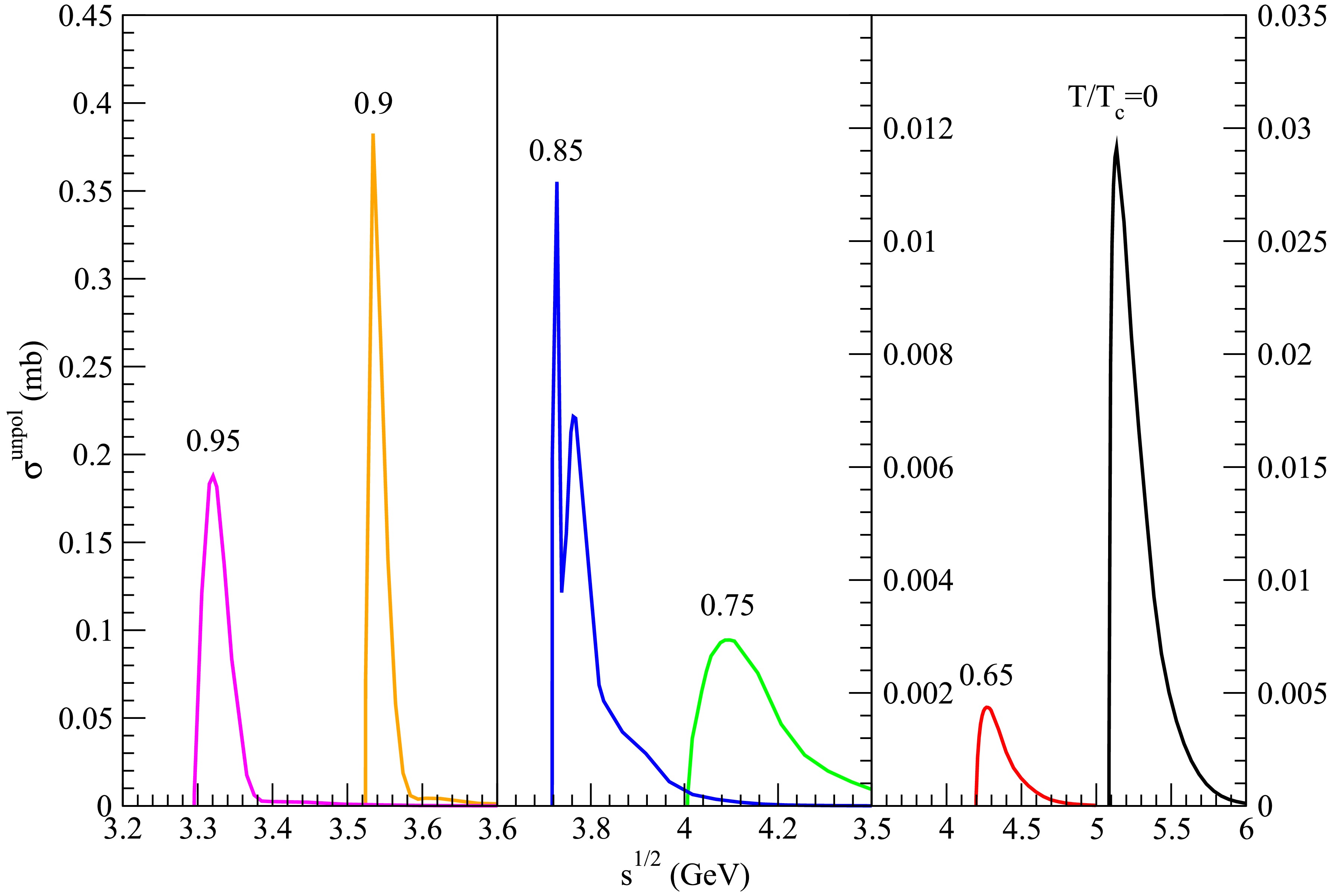
Figure 8. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K^\ast \psi(4160) $ at various temperatures.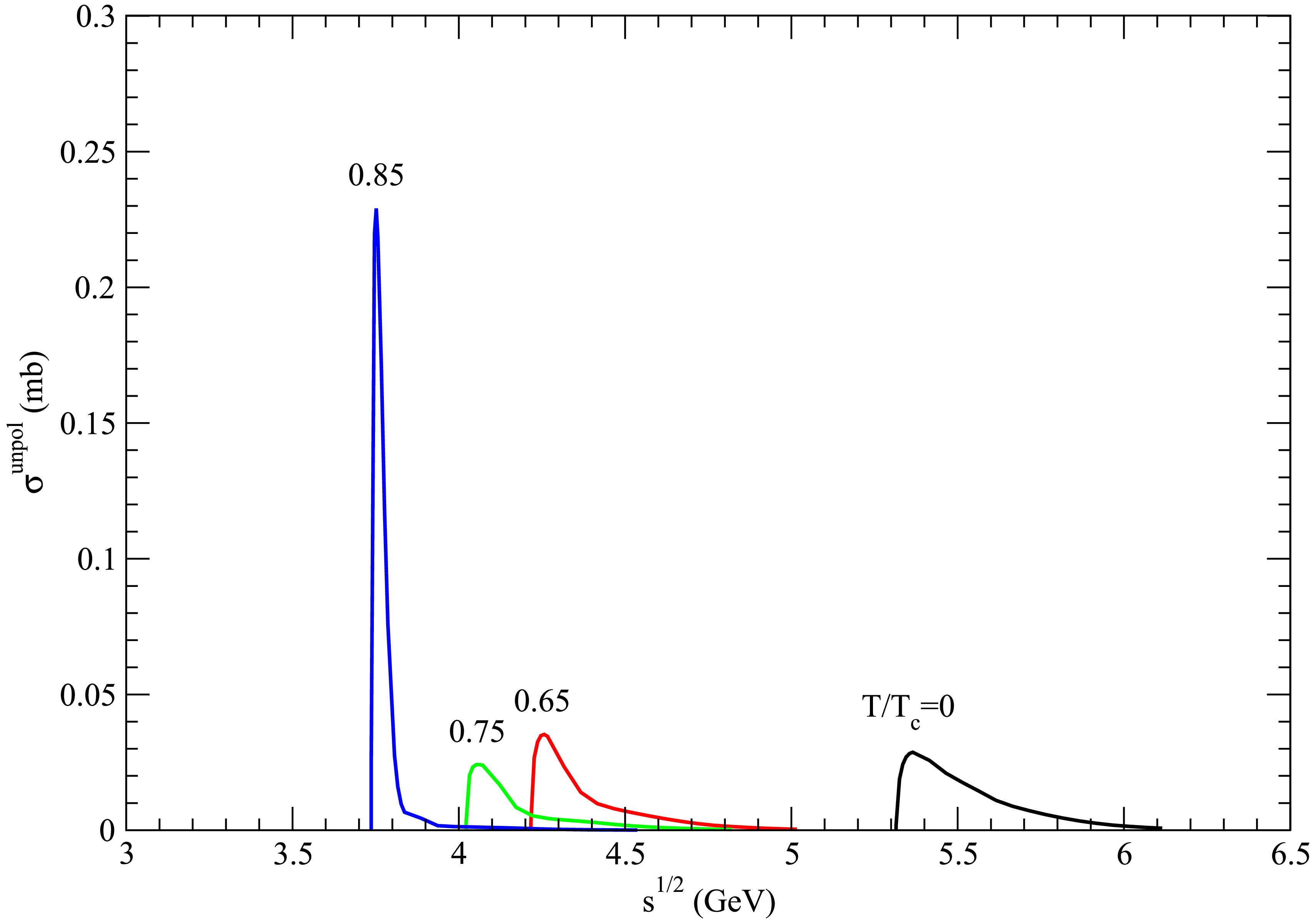
Figure 9. (color online) Cross sections for
$ D_s^+ \bar{D}^{\ast} \rightarrow K^\ast \psi(4415) $ at various temperatures.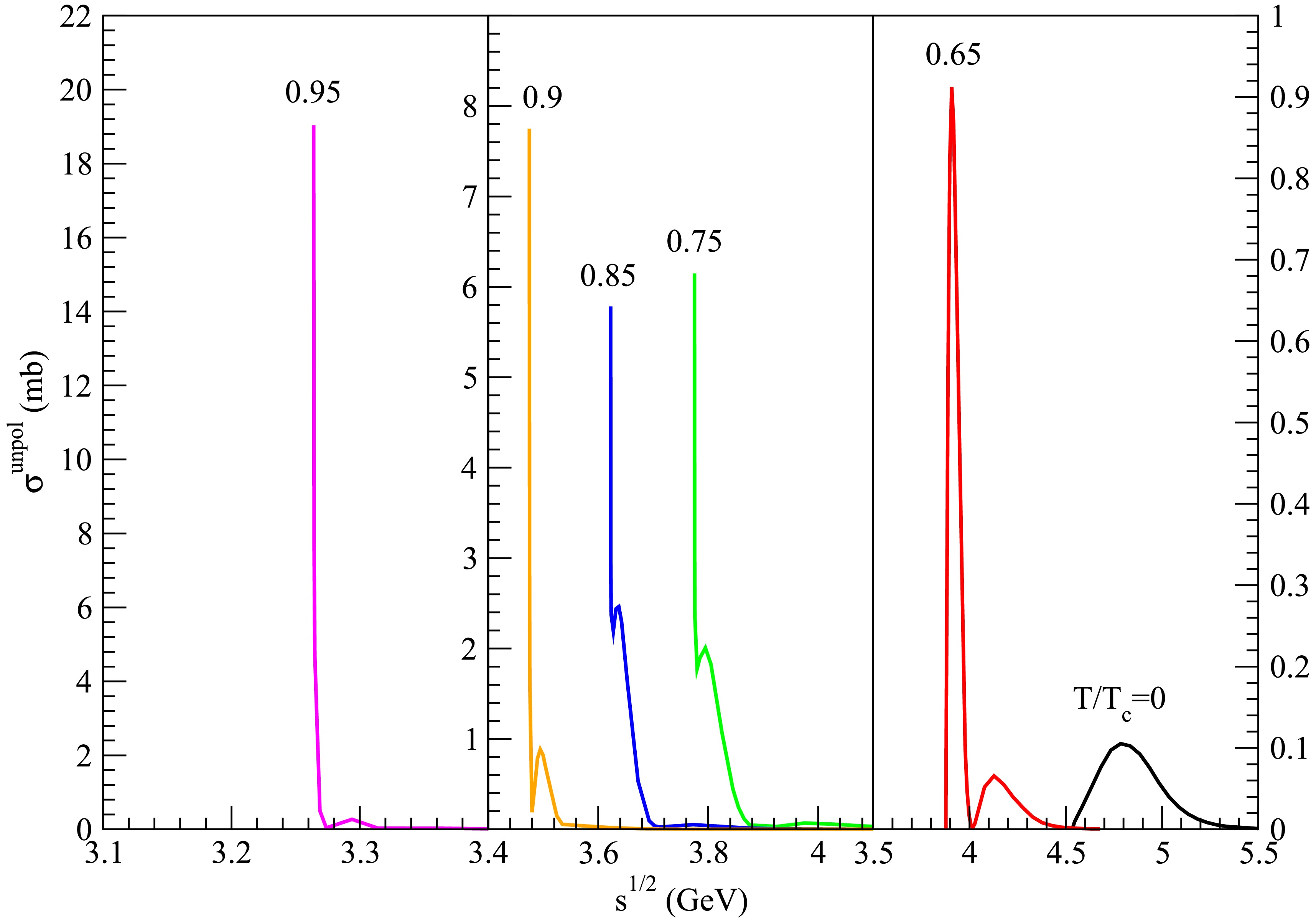
Figure 10. (color online) Cross sections for
$ D_s^{\ast +} \bar{D} \rightarrow K \psi(4040) $ at various temperatures.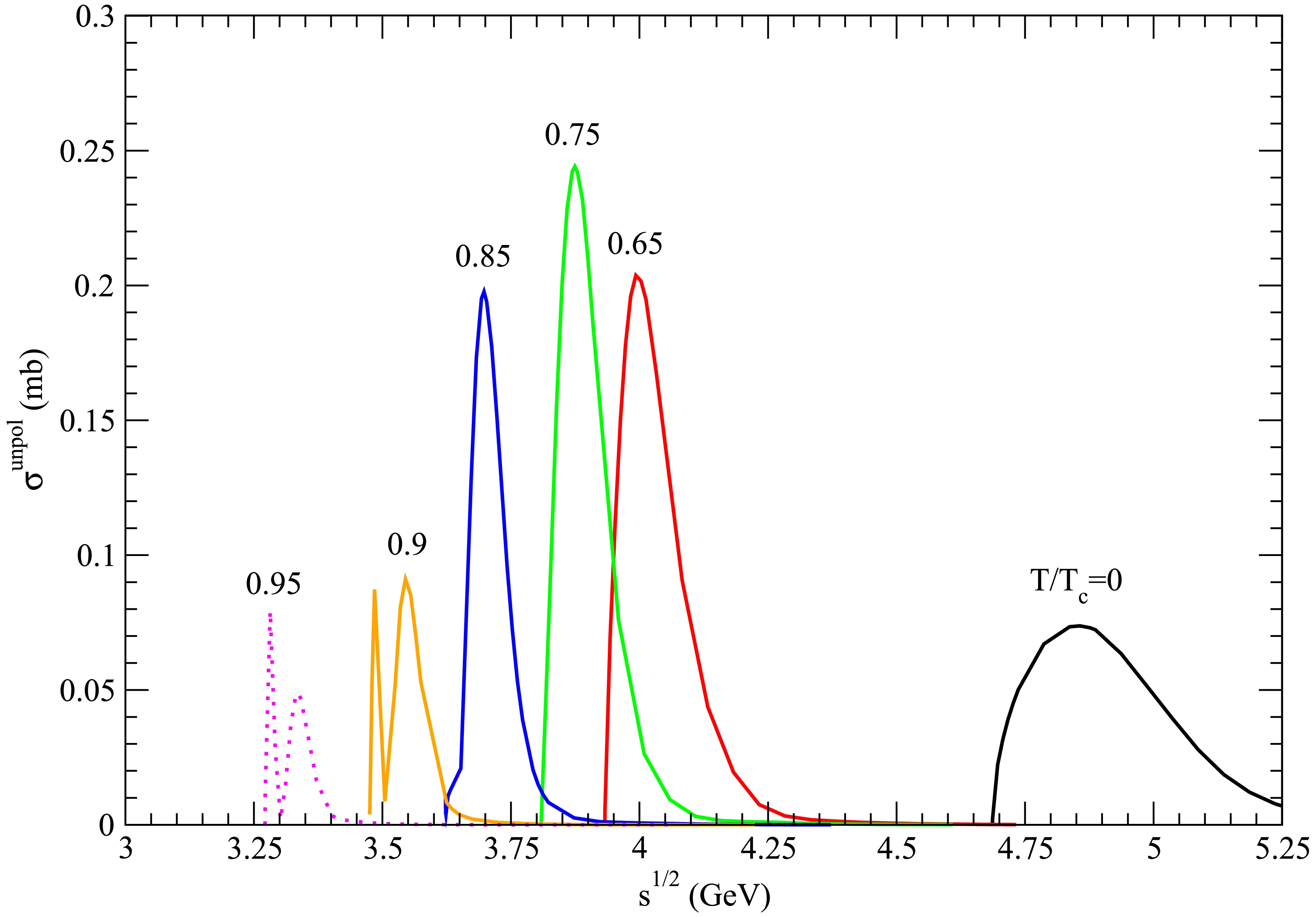
Figure 11. (color online) Cross sections for
$ D_s^{\ast +} \bar{D} \rightarrow K \psi(4160) $ at various temperatures.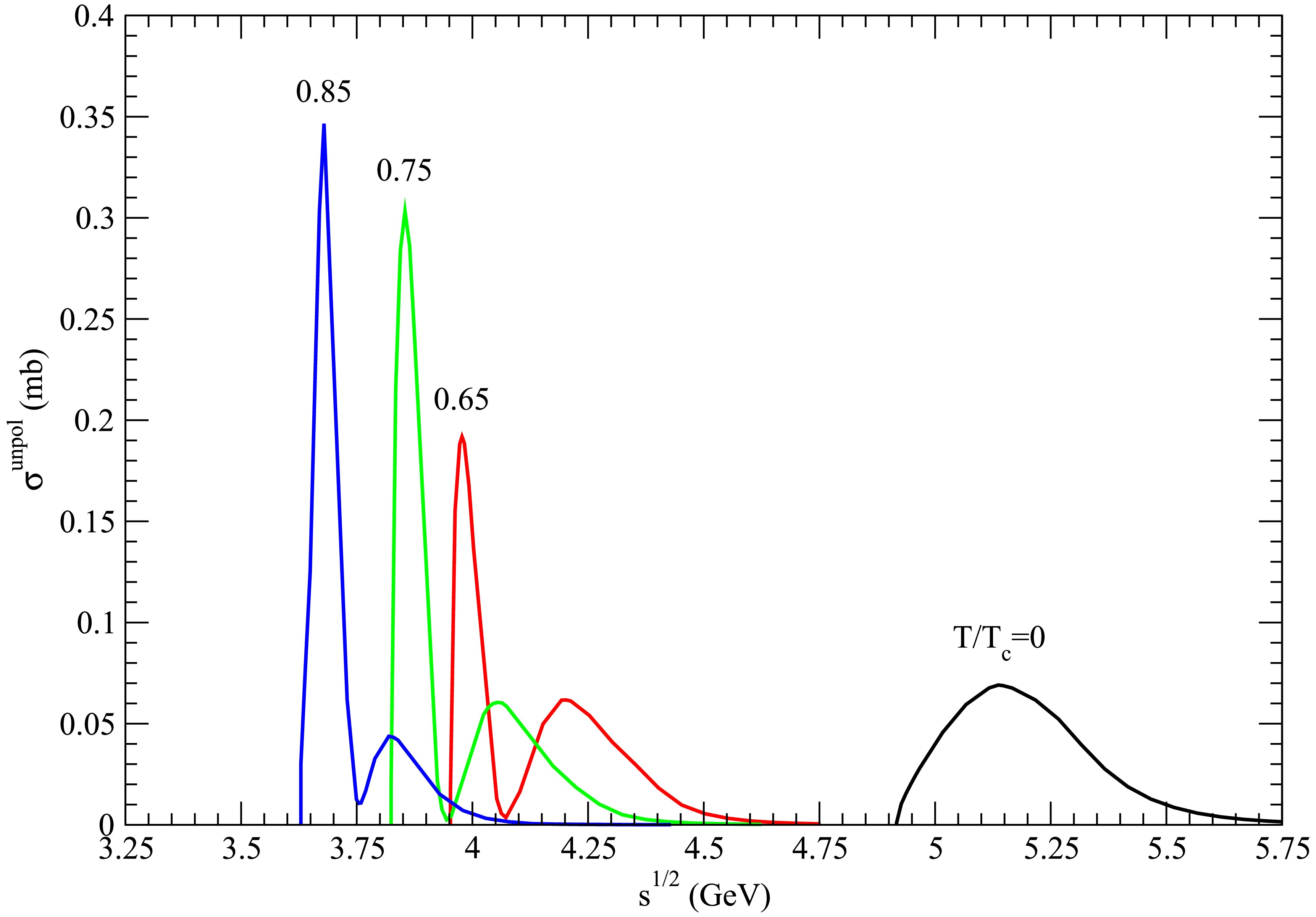
Figure 12. (color online) Cross sections for
$ D_s^{\ast +} \bar{D} \rightarrow K \psi(4415) $ at various temperatures.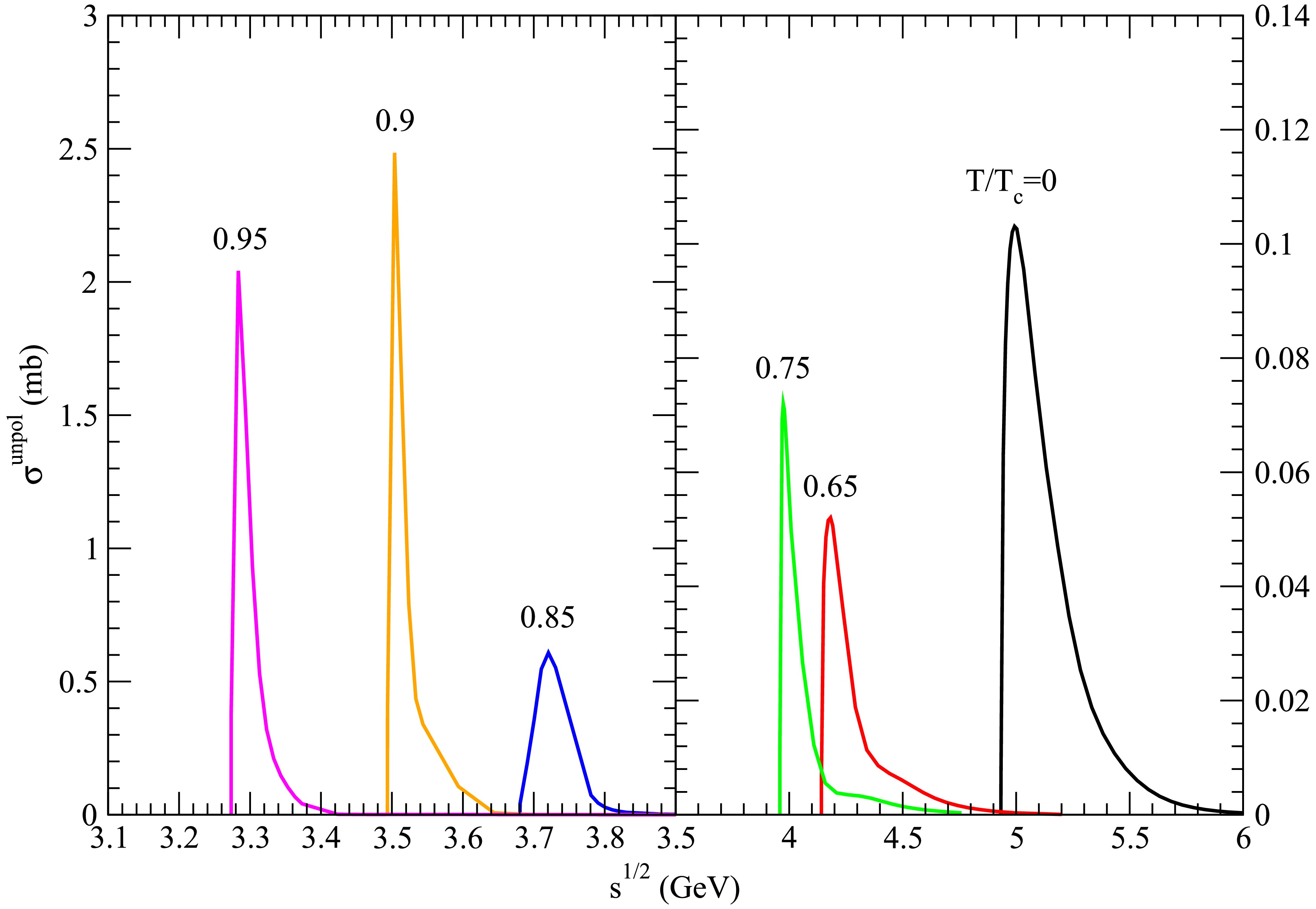
Figure 13. (color online) Cross sections for
$ D_s^{\ast +} \bar{D} \rightarrow K^\ast \psi(4040) $ at various temperatures.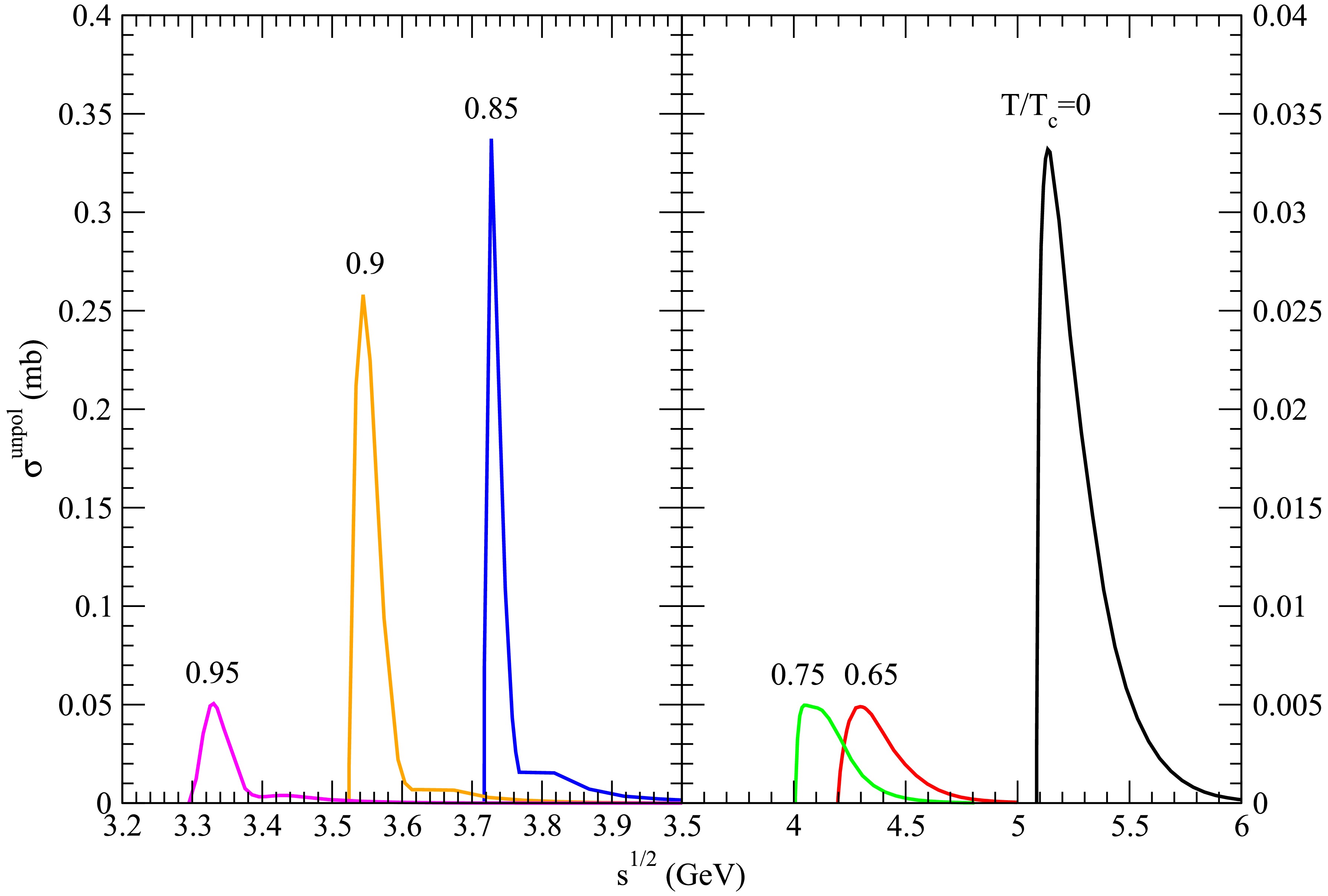
Figure 14. (color online) Cross sections for
$ D_s^{\ast +} \bar{D} \rightarrow K^\ast \psi(4160) $ at various temperatures.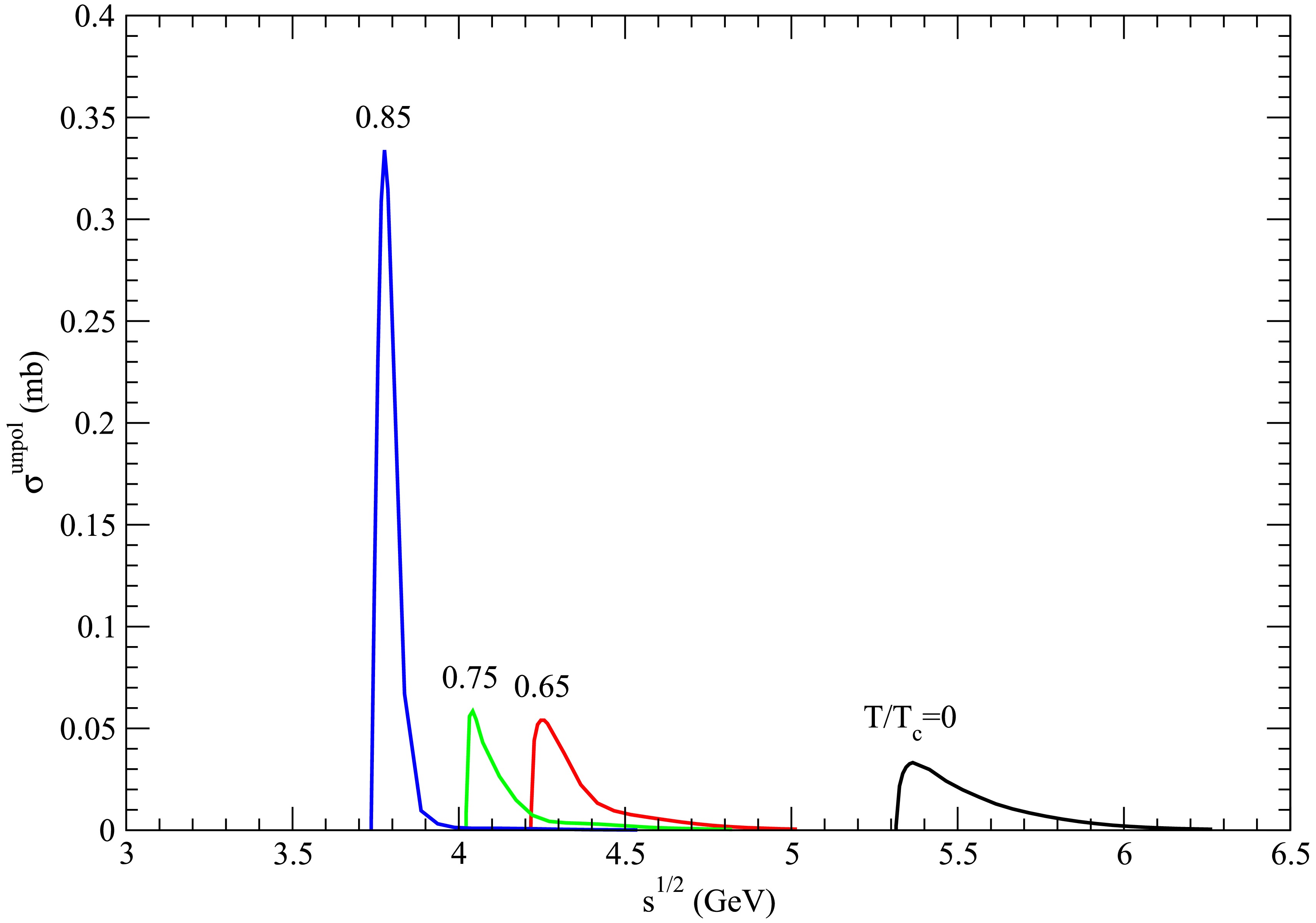
Figure 15. (color online) Cross sections for
$ D_s^{\ast +}\bar{D} \rightarrow K^\ast \psi(4415) $ at various temperatures.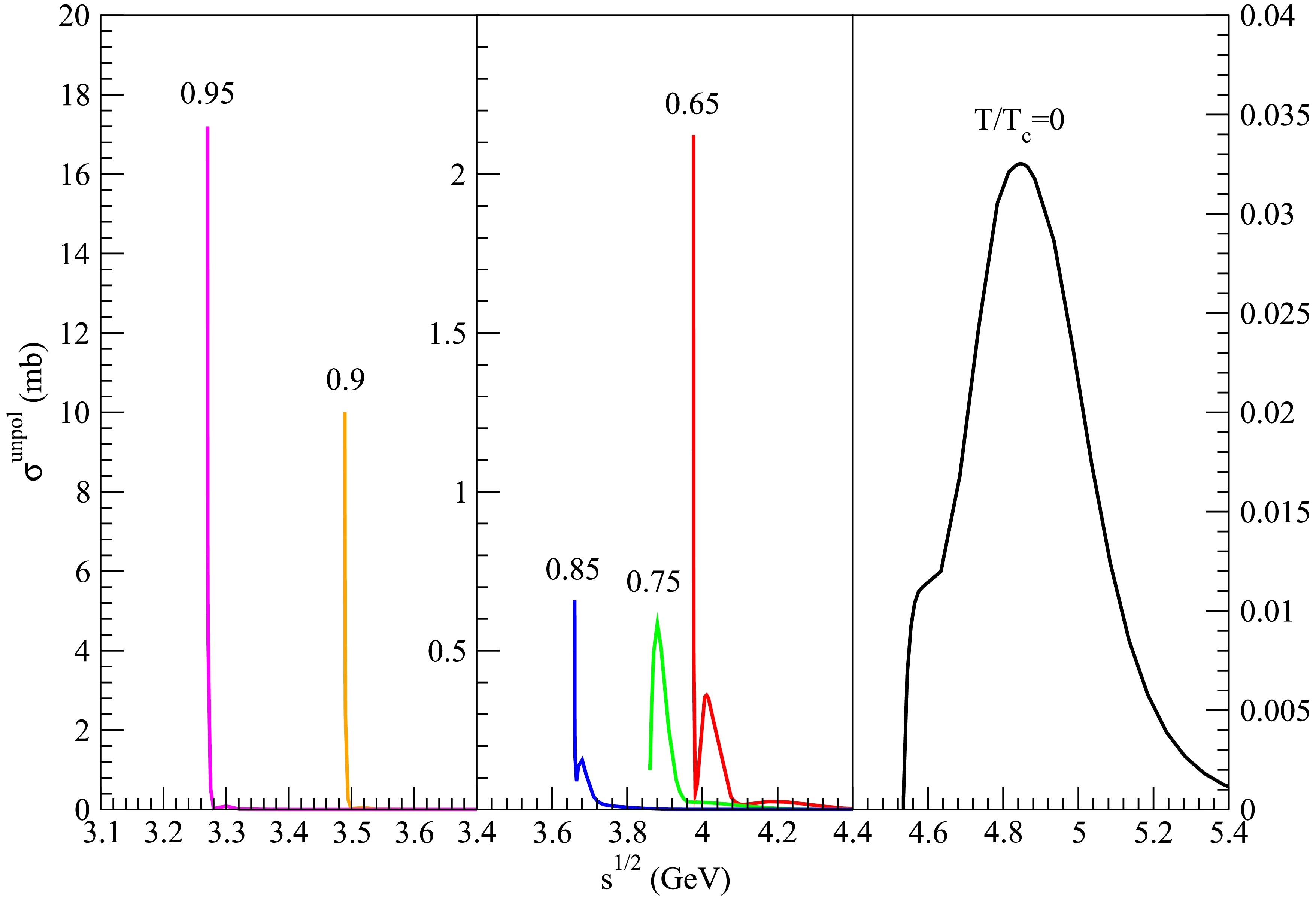
Figure 16. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K \psi(4040) $ at various temperatures.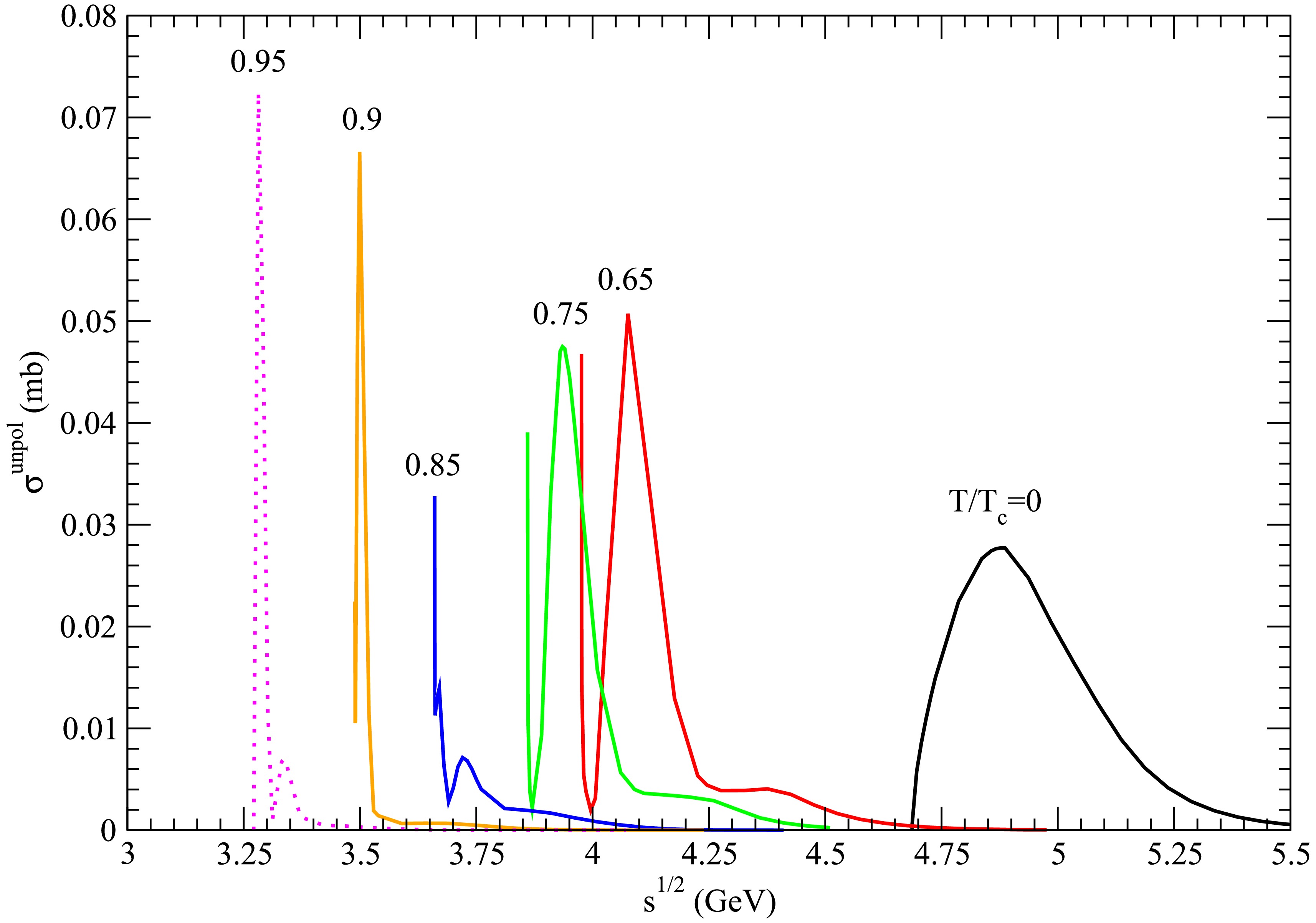
Figure 17. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K \psi(4160) $ at various temperatures.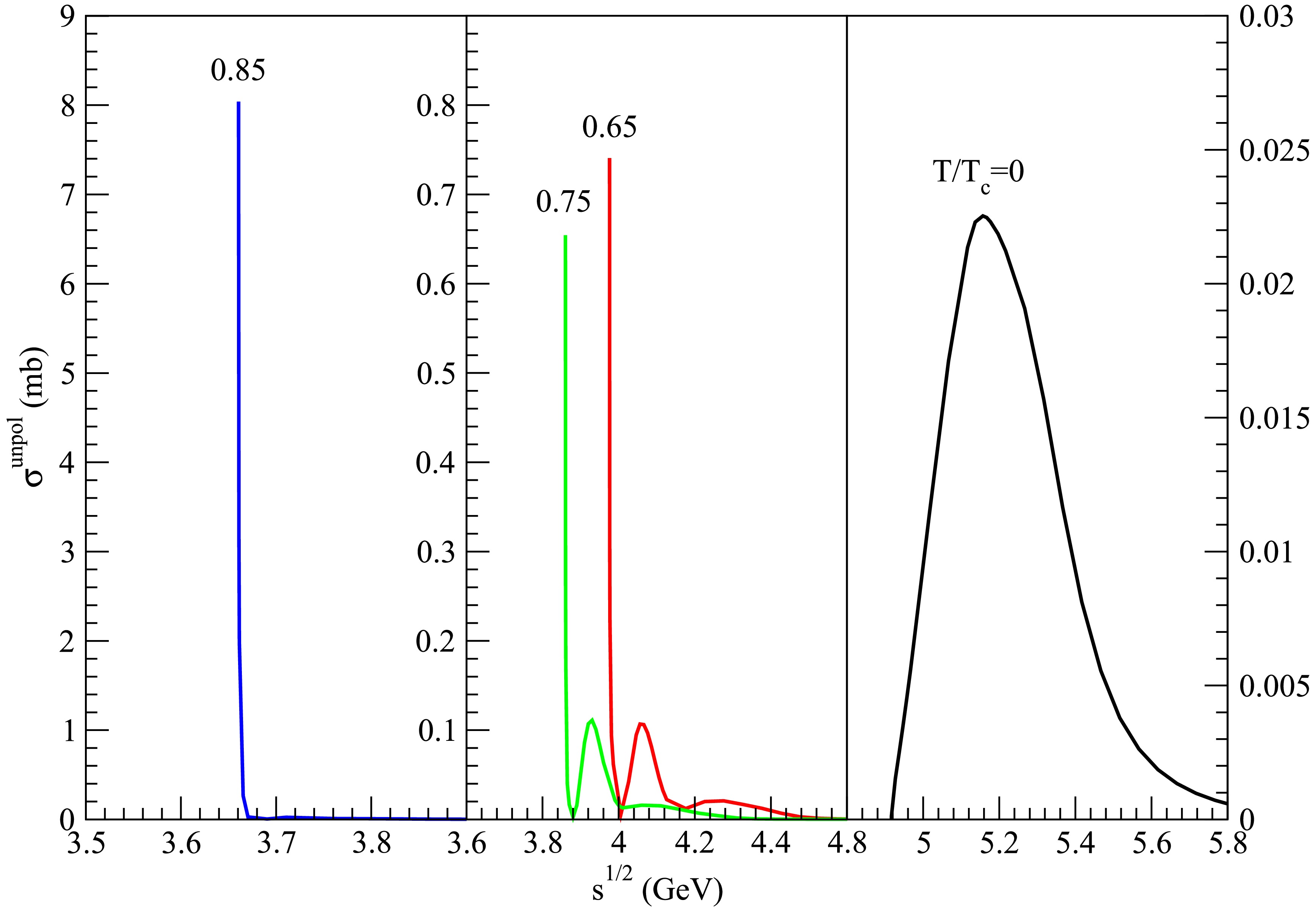
Figure 18. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K \psi(4415) $ at various temperatures.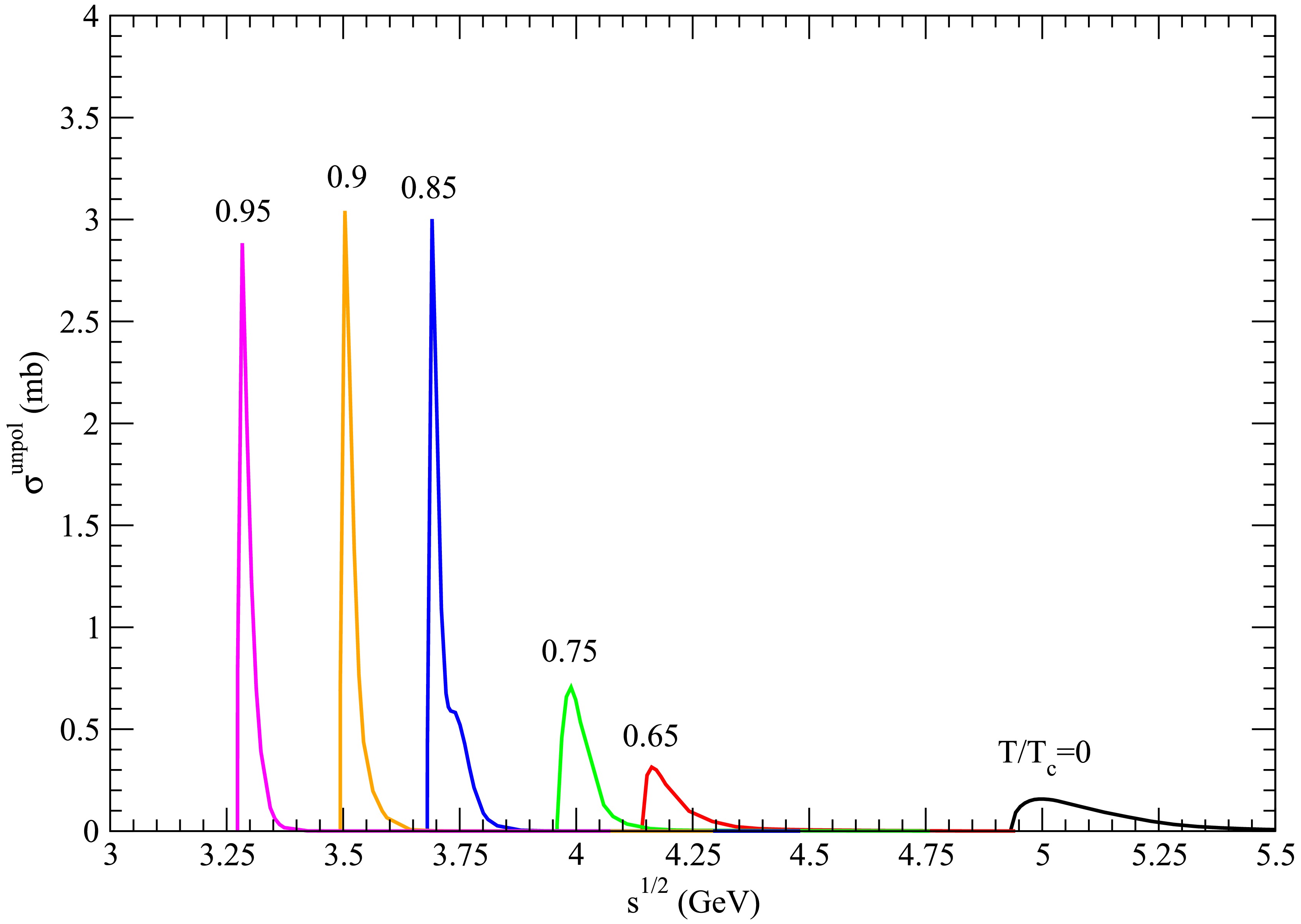
Figure 19. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K^\ast \psi(4040) $ at various temperatures.
Figure 20. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K^\ast \psi(4160) $ at various temperatures.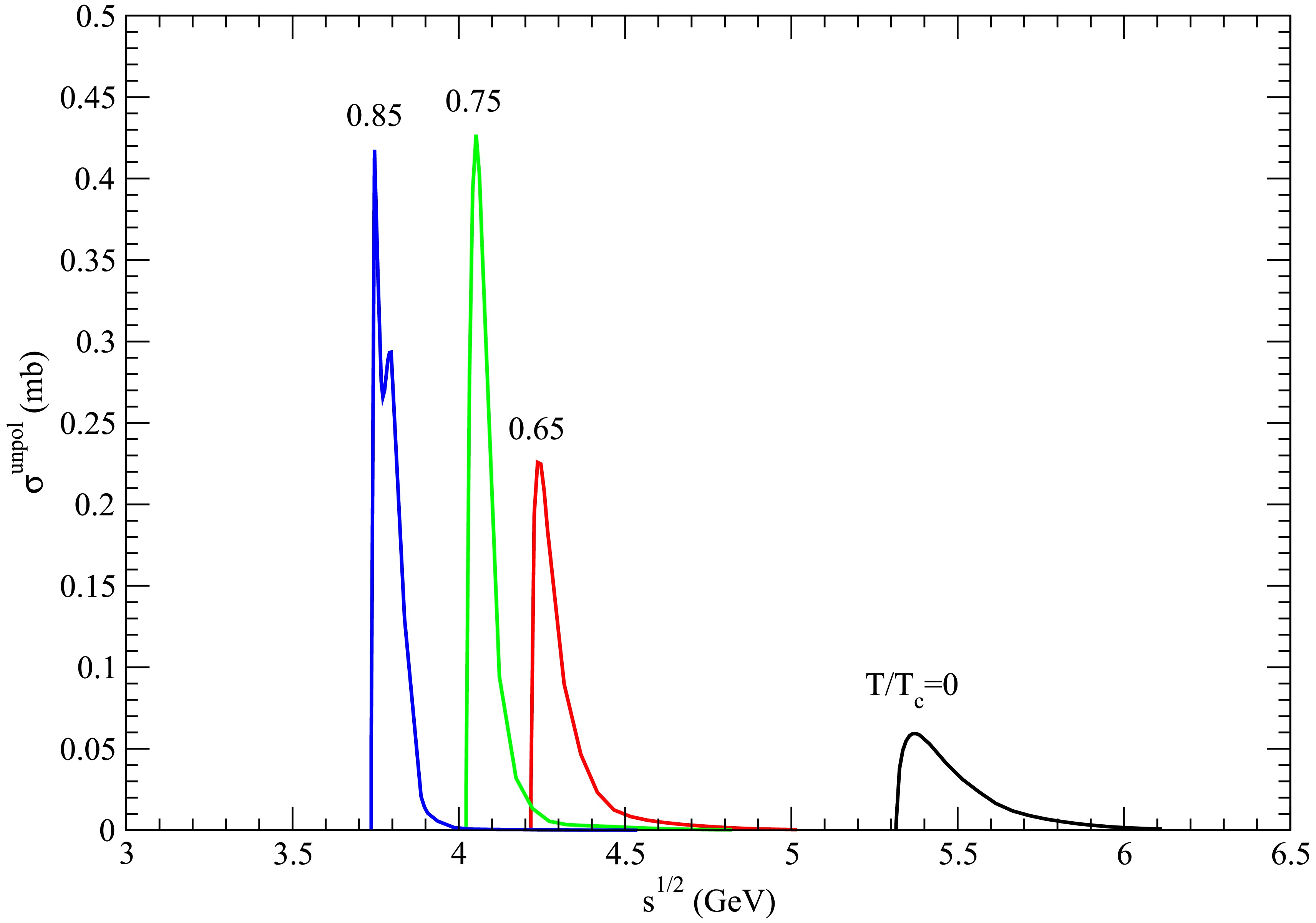
Figure 21. (color online) Cross sections for
$ D_s^{\ast +} \bar{D}^{\ast} \rightarrow K^\ast \psi(4415) $ at various temperatures.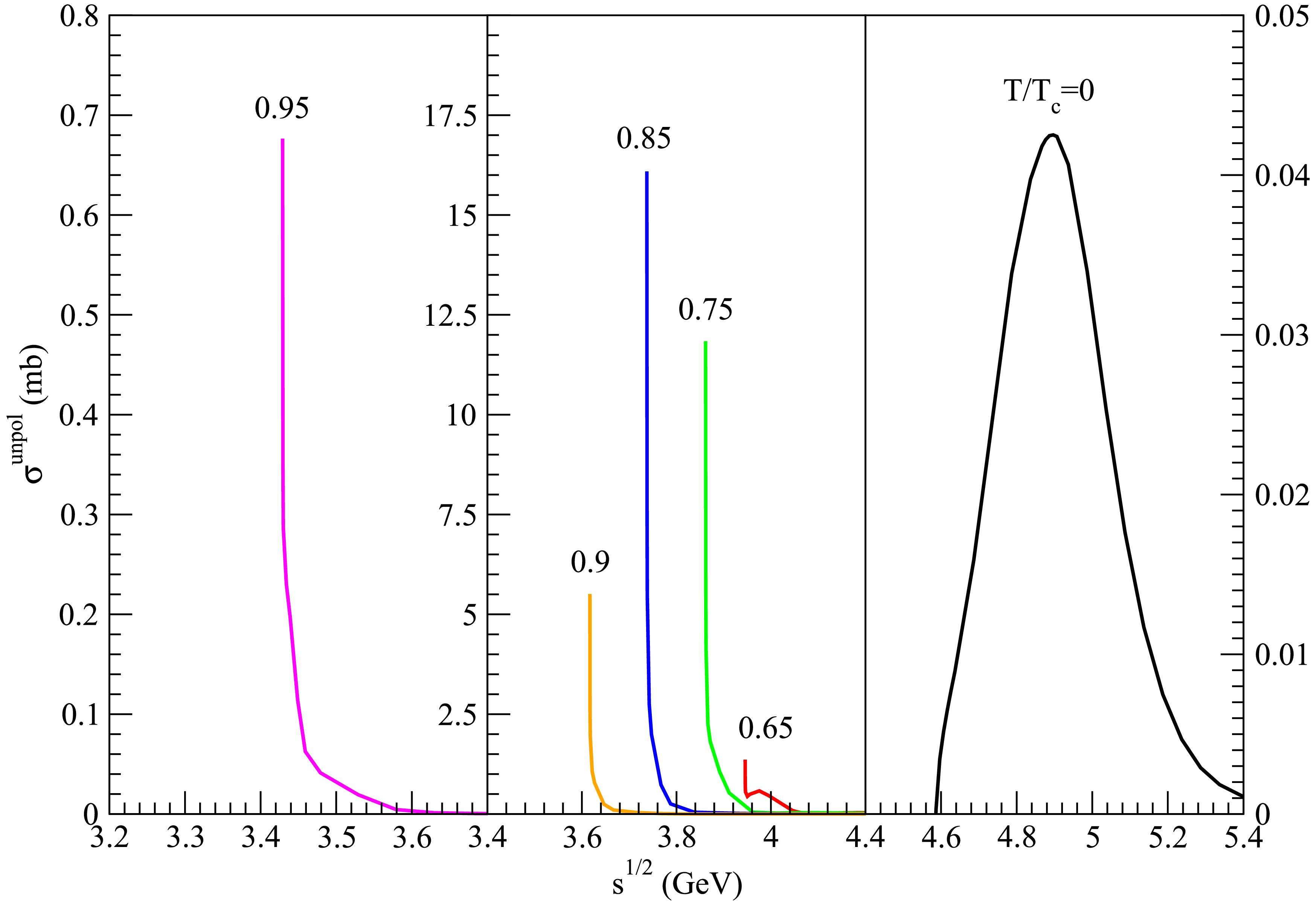
Figure 22. (color online) Cross sections for
$ D_s^+ D_s^{\ast -} \rightarrow \eta \psi(4040) $ at various temperatures.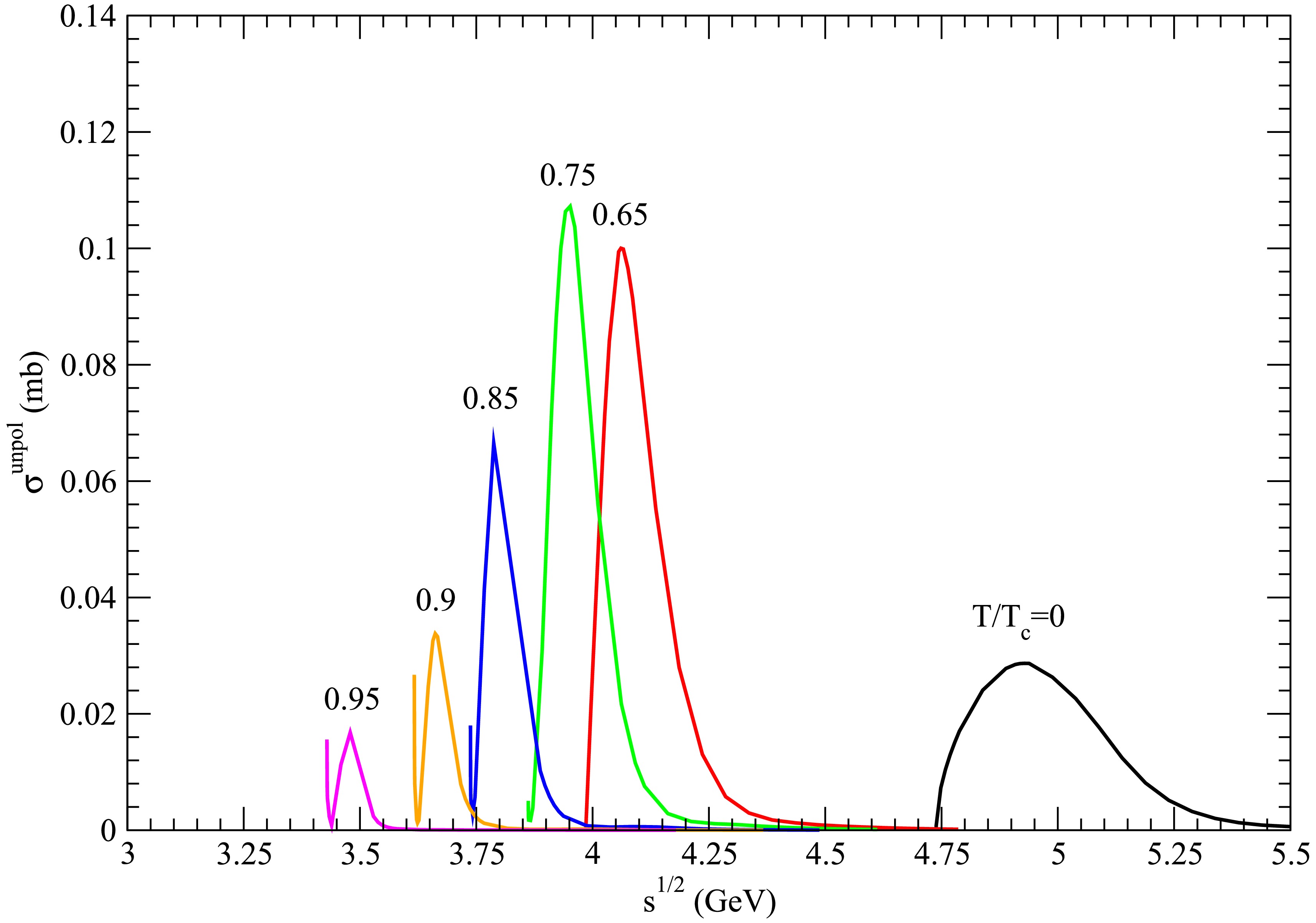
Figure 23. (color online) Cross sections for
$ D_s^+ D_s^{\ast -} \rightarrow \eta \psi(4160) $ at various temperatures.
Figure 24. (color online) Cross sections for
$ D_s^+ D_s^{\ast -} \rightarrow \eta \psi(4415) $ at various temperatures.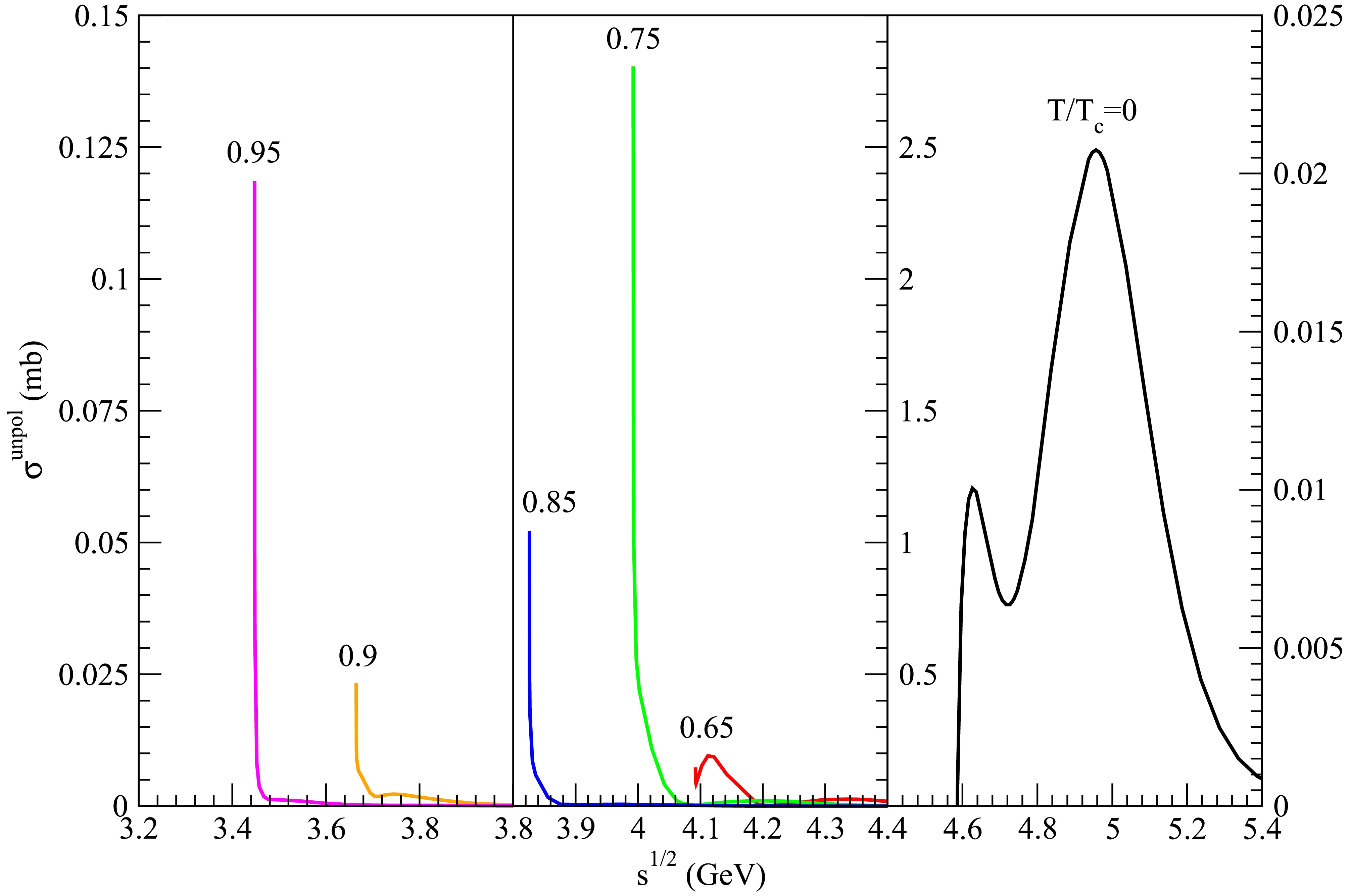
Figure 25. (color online) Cross sections for
$ D_s^{\ast +} D_s^{\ast -} \rightarrow \eta \psi(4040) $ at various temperatures.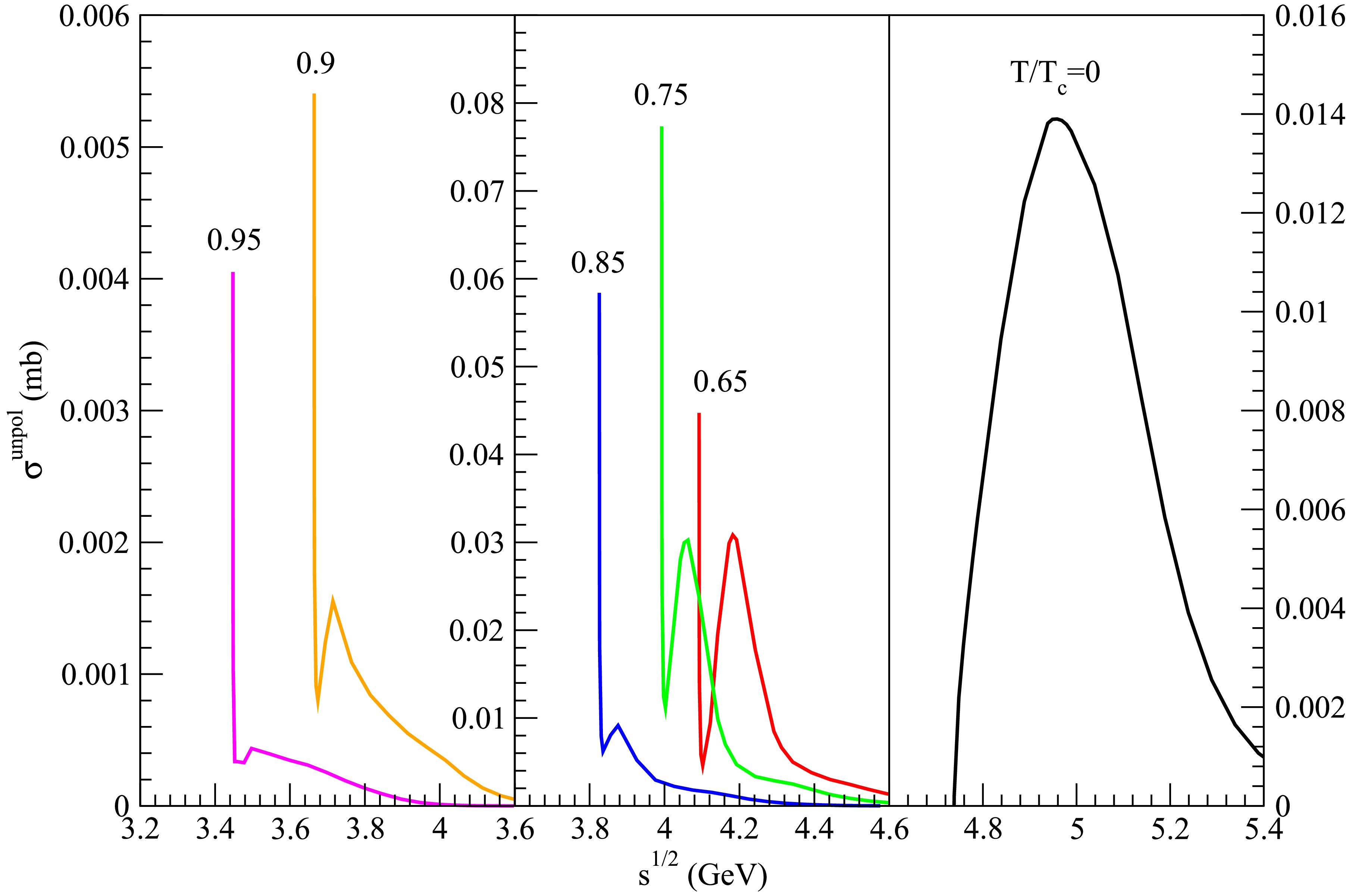
Figure 26. (color online) Cross sections for
$ D_s^{\ast +} D_s^{\ast -} \rightarrow \eta \psi(4160) $ at various temperatures.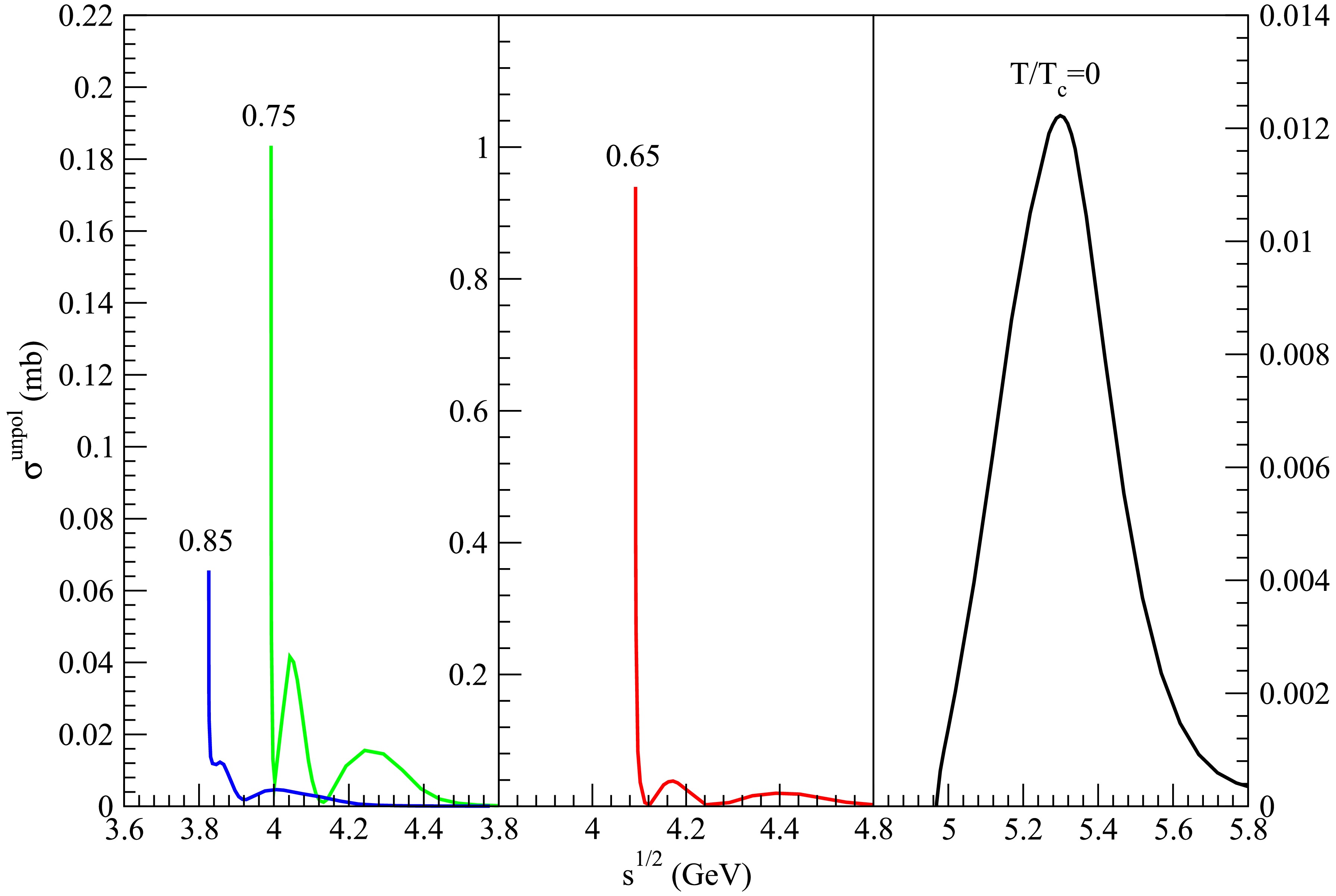
Figure 27. (color online) Cross sections for
$ D_s^{\ast +} D_s^{\ast -} \rightarrow \eta \psi(4415) $ at various temperatures.For the reaction
$ c\bar{q}_2 + q_1\bar{c} \to q_1\bar{q}_2 + c\bar{c} $ , the absolute values of the three-dimensional momenta of mesons$ c\bar{q}_2 $ and$ q_1\bar{q}_2 $ in the center-of-mass frame are given by$ \mid \vec{P} \mid =\frac {1}{2} \sqrt {\frac {(s-m_{c\bar{q}_2}^2-m_{q_1\bar c}^2)^2 -4m_{c\bar{q}_2}^2m_{q_1\bar c}^2}{s}}, $

$ \mid \vec{P}^\prime \mid =\frac {1}{2} \sqrt {\frac {(s-m_{q_1\bar{q}_2}^2-m_{c\bar c}^2)^2 -4m_{q_1\bar{q}_2}^2m_{c\bar c}^2}{s}}. $

If the sum of the masses of the two initial mesons of a reaction is smaller than that of the two final mesons, the reaction is endothermic. The threshold energy equals the sum of the masses of the two final mesons. At the threshold,
$ \mid \vec{P} \mid \neq 0 $ ,$ \mid \vec{P}^\prime \mid = 0 $ , and the factor$ \mid \vec{P}^\prime \mid / \mid \vec{P} \mid $ in Eq. (7) yields$ \sigma^{\rm{unpol}}=0 $ . Given a temperature, every endothermic reaction has at least a peak cross section. The initial mesons require kinetic energies to satisfy energy conservation and start the reaction, and a certain amount of the kinetic energies are converted into the masses of the final mesons. If the sum of the masses of the two initial mesons is larger than that of the two final mesons, the reaction is exothermic. The threshold energy equals the sum of the masses of the two initial mesons. At the threshold,$ \mid \vec{P} \mid = 0 $ ,$ \mid \vec{P}^\prime \mid \neq 0 $ , and$ \mid \vec{P}^\prime \mid / \mid \vec{P} \mid $ in Eq. (7) yields$ \sigma^{\rm{unpol}}=+\infty $ . Even slowly-moving initial mesons may start the reaction, and a certain amount of the masses of the initial mesons are converted into the kinetic energies of the final mesons. Because meson masses decrease with increasing temperature, the sum of the masses of the two initial mesons may be smaller than the one of the two final mesons at one temperature but may be larger than the one of the two final mesons at another. Therefore, a reaction may be endothermic at one temperature and exothermic at another. This phenomenon occurs to$ D_s^+ \bar{D}^* \to K \psi(4040) $ in Fig. 4,$ D_s^{*+} \bar{D} \to K \psi(4040) $ in Fig. 10,$ D_s^{*+} \bar{D} \to K \psi(4160) $ in Fig. 11,$ D_s^{*+} \bar{D}^* \to K \psi(4040) $ in Fig. 16,$ D_s^{*+} \bar{D}^* \to K \psi(4160) $ in Fig. 17,$D_s^{*+} \bar{D}^* \to K \psi(4415)$ in Fig. 18,$ D_s^+ D_s^{*-} \to \eta \psi(4040) $ in Fig. 22,$ D_s^+ D_s^{*-} \to \eta \psi(4160) $ in Fig. 23,$ D_s^+ D_s^{*-} \to \eta \psi(4415) $ in Fig. 24,$ D_s^{*+} D_s^{*-} \to \eta \psi(4040) $ in Fig. 25,$ D_s^{*+} D_s^{*-} \to \eta \psi(4160) $ in Fig. 26, and$ D_s^{*+} D_s^{*-} \to \eta \psi(4415) $ in Fig. 27.The Schrödinger equation with the potential given in Eq. (10) yields energy eigenvalues and quark-antiquark relative-motion wave functions in coordinate space. Through the Schrödinger equation, a meson mass is given as a sum of the quark mass, the antiquark mass, and an eigenvalue. Because the potential decreases with increasing temperature, eigenvalues and meson masses decrease [18]. Threshold energies, which are the sum of the masses of the two final (initial) mesons for endothermic (exothermic) reactions, decrease with increasing temperature, as shown in Figs. 1−27. The reduced amounts of meson masses are different for different mesons. For example, from
$ T=0 $ to$ T=0.85T_{\rm{c}} $ the$ K^\ast $ and$ \psi(4040) $ masses are reduced by 0.399 GeV and 0.859 GeV, respectively, and the threshold energy of$ D_s^+ \bar{D} \to K^\ast \psi(4040) $ is reduced by 1.258 GeV.When
$ \sqrt s $ increases from the threshold energy,$ \mid \vec{P} \mid $ of any endothermic reaction increases from a nonzero value,$ \mid \vec{P}^\prime \mid $ increases from zero, and$ \mid \vec{P}^\prime \mid / \mid \vec{P} \mid $ causes a rapid increase in the cross section close to the threshold energy. Because every mesonic quark-antiquark relative momentum is a linear combination of$ \vec{P} $ and$ \vec{P}^\prime $ , its absolute value increases with increasing$ \sqrt s $ . The radial wave functions of the quark-antiquark relative motion of D,$ \bar D $ ,$ D^* $ ,$ \bar{D}^* $ ,$ D_s^+ $ ,$ D_s^- $ ,$ D_s^{*+} $ ,$ D_s^{*-} $ , K,$ \bar K $ ,$ K^* $ ,$ \bar{K}^* $ , and η mesons are decreasing functions of relative momenta. The radial wave functions of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons have nodes and are decreasing functions of large relative momenta. The transition amplitudes may increase and then decrease rapidly with increasing$ \sqrt s $ . The increasing$ \mid \vec{P}^\prime \mid / \mid \vec{P} \mid $ and decreasing transition amplitudes produce a narrow peak in the cross-section curve near the threshold energy.Meson masses at zero temperature show that the sum of the masses of the two initial mesons of any reaction listed in Sec. II is smaller than that of the two final mesons, and the reaction is endothermic. Concerning three reactions such as
$ D_s^+ \bar{D} \to K^\ast \psi(4040) $ ,$ D_s^+ \bar{D} \to K^\ast \psi(4160) $ , and$ D_s^+ \bar{D} \to K^\ast \psi(4415) $ , which have the same initial mesons and one identical final meson, a characteristic observed in Figs. 1−27 is that the peak cross section of producing$ \psi(4040) $ is larger than those of producing$ \psi(4160) $ and$ \psi(4415) $ and the peak cross section of producing$ \psi(4160) $ is similar to the one of producing$ \psi(4415) $ . The$ \mid \vec{P}^\prime \mid / s\mid \vec{P} \mid $ value corresponding to the peak cross section of producing$ \psi(4040) $ is larger than that of producing$ \psi(4160) $ , and the latter is larger than that of producing$ \psi(4415) $ .$ \mid \vec{P}^\prime \mid / s\mid \vec{P} \mid $ in Eq. (7) reveals that the peak cross section of producing$ \psi(4040) $ is larger than those of producing$ \psi(4160) $ and$ \psi(4415) $ . In Eqs. (8) and (9), the wave function$ \psi_{c\bar c} $ contains the$ c\bar c $ relative-motion wave function, which is the product of the radial wave function of the relative motion and the spherical harmonics$ Y_{L_{c\bar c}M_{c\bar c}} $ , where$ L_{c\bar c} $ is the orbital-angular-momentum quantum number and$ M_{c\bar c} $ is the magnetic projection quantum number. According to the quantum numbers of$ \psi(4160) $ and$ \psi(4415) $ mesons, the relative-motion wave functions of$ \psi(4160) $ and$ \psi(4415) $ contain$ Y_{2M_{c\bar c}} $ ($ M_{c\bar c} $ =-2, -1, 0, 1, 2) and$ Y_{00} $ , respectively. Because the mass of$ \psi(4160) $ is smaller than that of$ \psi(4415) $ , we expect that producing$ \psi(4160) $ is easier than producing$ \psi(4415) $ . However, the cross section for producing$ \psi(4160) $ is more reduced by$ Y_{2M_{c\bar c}} $ than the cross section for producing$ \psi(4415) $ by$ Y_{00} $ . Consequently, the peak cross section of producing$ \psi(4160) $ is similar to the one of producing$ \psi(4415) $ .Figures 1−21 show that, below the critical temperature, the following reactions are endothermic:
$ D_s^+ \bar{D} \to K^\ast \psi(4040), D_s^+ \bar{D} \to K^\ast \psi(4160), D_s^+ \bar{D} \to K^\ast \psi(4415), $

$ D_s^+ \bar{D}^\ast \to K \psi(4160), D_s^+ \bar{D}^\ast \to K \psi(4415), D_s^+ \bar{D}^\ast \to K^\ast \psi(4040), $

$ D_s^+ \bar{D}^\ast \to K^\ast \psi(4160), D_s^+ \bar{D}^\ast \to K^\ast \psi(4415), D_s^{\ast +} \bar{D} \to K \psi(4415), $

$ D_s^{\ast +} \bar{D} \to K^\ast \psi(4040), D_s^{\ast +} \bar{D} \to K^\ast \psi(4160), D_s^{\ast +} \bar{D} \to K^\ast \psi(4415), $

$\begin{aligned}& D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4040),\quad D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4160),\\& D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4415). \end{aligned}$

As the temperature increases from zero, confinement shown by the potential in Eq. (10) becomes increasingly weaker, the Schrödinger equation yields increasing meson radii, and mesonic quark-antiquark states become increasingly looser. On one hand, the weakening confinement with increasing temperature makes combining final quarks and antiquarks into final mesons more difficult, and thus reduces cross sections. On the other hand, the increasing radii of initial mesons cause increasing cross sections as the temperature increases. The two factors determine the change in the peak cross section with respect to the temperature, which is shown in Figs. 1−21.
The
$ K^\ast $ meson is a loose bound state and is more affected by confinement. Regarding the six reactions,$ D_s^+ \bar{D} \to K^\ast \psi(4040), D_s^+ \bar{D} \to K^\ast \psi(4160), D_s^+ \bar{D} \to K^\ast \psi(4415), $

$\begin{aligned}& D_s^+ \bar{D}^\ast \to K^\ast \psi(4040), \quad D_s^+ \bar{D}^\ast \to K^\ast \psi(4160),\\& D_s^+ \bar{D}^\ast \to K^\ast \psi(4415), \end{aligned}$

at
$ T/T_{\rm{c}}=0.65 $ and 0.75, the reduced amount of the cross section due to the weakening confinement exceeds the increased amount of the cross section due to the increasing radii of the initial mesons. Thus, the peak cross sections decrease as$ T/T_{\rm{c}} $ increases from 0.65 to 0.75. The six reactions have the characteristic that the peak cross sections initially decrease and then generally increase as the temperature increases from$ 0.65T_{\rm{c}} $ . Note that the six reactions have the initial meson$ D_s^+ $ . If we replace the$ D_s^+ $ meson by the$ D_s^{*+} $ meson, which has a radius larger than the$ D_s^+ $ meson, the reduced amount of the cross section due to the weakening confinement is smaller than the increased amount of the cross section due to the increasing radii of the initial mesons. Thus, the peak cross sections of the following reactions$\begin{aligned}& D_s^{\ast +} \bar{D} \to K^\ast \psi(4040),\quad D_s^{\ast +} \bar{D} \to K^\ast \psi(4160),\\& D_s^{\ast +} \bar{D} \to K^\ast \psi(4415), \end{aligned}$

$\begin{aligned}& D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4040), \quad\; D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4160), \\& D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4415), \end{aligned}$

increase as
$ T/T_{\rm{c}} $ increases from 0.65 to 0.75. These reactions have the characteristic that the peak cross sections initially increase and then decrease as the temperature increases from$ 0.65T_{\rm{c}} $ .The K meson is a tight bound state and is less affected by confinement. For the three reactions,
$ D_s^+ \bar{D}^\ast \to K \psi(4160),\; D_s^+ \bar{D}^\ast \to K \psi(4415), \; D_s^{\ast +} \bar{D} \to K \psi(4415), $

at
$ T/T_{\rm{c}}=0.65 $ and 0.75, the decrease in cross sections due to the weakening confinement cannot balance the increase in cross sections due to the increasing radii of the initial mesons. Thus, the peak cross sections increase as$ T/T_{\rm{c}} $ increases from 0.65 to 0.75. The three reactions have the characteristic that the peak cross sections initially increases and then decreases as the temperature increases from$ 0.65T_{\rm{c}} $ .Now, we examine Fig. 4, Fig. 10, Fig. 11, Figs. 16−18, and Figs. 22−27 in which reactions are endothermic at some temperatures and exothermic at other temperatures. The final light-quark mesons of the reactions are the K and η mesons. The η meson is also a tight bound state and is less affected by confinement. Because the cross sections of exothermic reactions are infinite at the threshold energy,
$ m_{c\bar{q}_2}+m_{q_1\bar{c}} $ , we start calculations of the cross sections at$ \sqrt{s}=m_{c\bar{q}_2}+m_{q_1\bar{c}} +\Delta \sqrt{s} $ with$ \Delta \sqrt{s} = 10^{-4} $ GeV. At$ \sqrt{s}=m_{c\bar{q}_2}+m_{q_1\bar{c}}+\Delta \sqrt{s} $ ,$ \frac{\vec{P}^{\; \prime 2}}{\vec{P}^2} \approx \frac{m_{c\bar{q}_2}+m_{q_1\bar{c}}-m_{q_1\bar{q}_2}-m_{c\bar{c}}} {\Delta \sqrt{s}} \frac{m_{q_1\bar{q}_2}m_{c\bar{c}}}{m_{c\bar{q}_2}m_{q_1\bar{c}}} \frac{m_{c\bar{q}_2}+m_{q_1\bar{c}}}{m_{q_1\bar{q}_2}+m_{c\bar{c}}} , $

which depends on the difference between the sum of the masses of the two initial mesons and the sum of the masses of the two final mesons. If the difference is not close to zero,
$ \mid \vec{P}^{\; \prime} \mid / \mid \vec{P} \mid $ is not small. When$ \sqrt s $ increases from the threshold energy,$ \mid \vec{P}^{\; \prime} \mid / \mid \vec{P} \mid $ decreases rapidly initially and then slowly to a minimum value and further increases slowly. The transition amplitudes may increase and then decrease with increasing$ \sqrt s $ . From these changes, Eq. (7) may yield a peak in the cross-section curve of an exothermic reaction such as$ D_s^+ \bar{D}^* \to K \psi (4040) $ in Fig. 4 in the region$ \sqrt{s} > m_{c\bar{q}_2}+m_{q_1\bar{c}} + 10^{-4} $ GeV. Therefore, every exothermic reaction has the characteristic that the cross section decreases rapidly and then may increase to form a peak when$ \sqrt s $ increases from the threshold energy. The cross sections shown in Fig. 4, Fig. 10, Fig. 11, Figs. 16−18, and Figs. 22−27 have the second characteristic that the peak cross sections increase initially and then generally decrease as the temperature increases from zero.Since the naive quark model was proposed by Gell-Mann and Zweig in 1964, the cross sections for meson-meson scattering were first considered to be four times that for quark-quark scattering. However, this additive picture of cross sections has been deemed to be approximate since QCD was established. One reason for this is that the cross section for elastic quark-quark scattering is not identical to the one for elastic quark-antiquark scattering, which involves quark-antiquark annihilation and creation [60]. Assuming that the wave functions of quarks and antiquarks are plane waves, the cross sections for quark-quark scattering and quark-antiquark scattering have been obtained in perturbative QCD. In low-energy meson-meson scattering, confinement of quarks and antiquarks in mesons must be considered. The wave functions of quarks and antiquarks are no longer plane waves, and the cross sections for meson-meson scattering appear similar to those in Figs. 1−27. In this work, low-energy meson-meson scattering produces two mesons. When the total center-of-mass energy (
$ \sqrt s $ ) increases, three, four, and more mesons are produced. Two-to-three meson-meson scattering, two-to-four meson-meson scattering, etc., lead to finite cross sections for meson-meson scattering.At zero temperature, all reactions shown in Figs. 1−27 are endothermic. However, at
$ T=0.65T_{\rm{c}} $ ,$ 0.75T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ,$ 0.9T_{\rm{c}} $ , or$ 0.95T_{\rm{c}} $ , a reaction may be endothermic or exothermic. Hence, we use the following two expressions to parametrize the numerical cross sections shown in Figs. 1−27:$ \begin{aligned}[b]& \sigma^{\rm{unpol}}(\sqrt {s},T) \\=\;& a_1 \left( \frac {\sqrt {s} -\sqrt {s_0}}{b_1} \right)^{c_1} \exp \left[ c_1 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}}{b_1} \right) \right] \\ & + a_2 \left( \frac {\sqrt {s} -\sqrt {s_0}}{b_2} \right)^{c_2} \exp \left[ c_2 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}}{b_2} \right) \right] , \end{aligned} $

(11) for endothermic reactions and
$ \begin{aligned}[b]& \sigma^{\rm{unpol}}(\sqrt {s},T) \\ =\;& \frac{{\vec {P'}}^2}{{\vec P}^2} \left\{a_1 \left( \frac {\sqrt {s} -\sqrt {s_0}}{b_1} \right)^{c_1} \exp \left[ c_1 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}}{b_1} \right) \right]\right. \\ & \left. + a_2 \left( \frac {\sqrt {s} -\sqrt {s_0}}{b_2} \right)^{c_2} \exp \left[ c_2 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}}{b_2} \right) \right]\right\} , \end{aligned} $

(12) for exothermic reactions.
$ \sqrt{s}_0 $ is the threshold energy. To use the two parametrizations in the master rate equations, we require the separation ($ d_0 $ ) between the peak's location on the$ \sqrt s $ axis and the threshold energy and square root ($ \sqrt{s_z} $ ) of the Mandelstam variable at which the cross section is 1/100 of the peak cross section. The values of$ a_1 $ ,$ b_1 $ ,$ c_1 $ ,$ a_2 $ ,$ b_2 $ ,$ c_2 $ ,$ d_0 $ , and$ \sqrt{s_z} $ are listed in Tables 1−9.Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K^\ast \psi(4040) $ 

0 0.01 0.03 0.42 0.08 0.07 0.51 0.06 5.88 0.65 0.011 0.183 1.91 0.023 0.0243 0.49 0.03 5.06 0.75 0.008 0.07 0.26 0.013 0.024 0.9 0.03 4.87 0.85 0.014 0.048 0.25 0.072 0.008 0.56 0.01 4.19 0.9 0.21 0.007 0.71 0.76 0.031 3 0.03 3.62 0.95 0.81 0.012 10.7 0.88 3.37 0.132 0.01 3.4 $ K^\ast \psi(4160) $ 

0 0.004 0.02 0.55 0.023 0.07 0.48 0.05 5.95 0.65 0.001 0.019 0.44 0.002 0.113 1.08 0.08 5.02 0.75 0.0001 0.0003 1.22 0.00142 0.0727 0.7 0.08 4.77 0.85 0.0016 0.024 0.29 0.0056 0.02 1.66 0.02 4.17 0.9 0.08 0.0003 0.43 0.34 0.0086 1.11 0.01 3.66 0.95 0.07 0.003 0.35 0.44 0.021 1.86 0.02 3.4 $ K^\ast \psi(4415) $ 

0 0.005 0.025 0.59 0.023 0.088 0.47 0.06 6.41 0.65 0.018 0.068 0.37 0.011 0.022 0.91 0.03 5.14 0.75 0.006 0.123 0.19 0.019 0.03 0.8 0.035 4.93 0.85 0.007 0.03 0.07 0.063 0.01 0.64 0.01 4.33 Table 1. Values of the parameters in Eq. (11) for
$ D_s^+ \bar{D} \to K^\ast \psi(4040) $ ,$ K^\ast \psi(4160) $ , and$ K^\ast \psi(4415) $ .$ a_1 $ and$ a_2 $ are in units of millibarns;$ b_1 $ ,$ b_2 $ ,$ d_0 $ , and$ \sqrt{s_{\rm{z}}} $ are in units of GeV;$ c_1 $ and$ c_2 $ are dimensionless.Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K \psi(4040) $ 

0 0.014 0.081 0.585 0.066 0.236 3.05 0.22 5.42 0.65 0.059 0.001 0.12 0.502 0.017 0.91 0.015 4.34 0.75 0.053 0.0001 0.03 0.905 0.0134 0.731 0.015 4.12 0.85 0.042 0.0306 0.276 1.38 0.0244 2.07 0.025 3.82 0.9 0.46 0.00058 0.57 2.38 0.0266 3.2 0.025 3.67 0.95 1.55 0.0009 0.48 1.14 0.0257 4.6 0.001 3.48 $ K \psi(4160) $ 

0 0.022 0.04 0.54 0.044 0.18 2.24 0.15 5.53 0.65 0.04 0.051 2.16 0.15 0.03 0.52 0.035 4.29 0.75 0.11 0.014 0.49 0.14 0.044 1.53 0.035 4.09 0.85 0.01 0.01 0.65 0.17 0.042 2.23 0.04 3.85 0.9 0.005 0.001 1.02 0.129 0.047 3.33 0.045 3.7 0.95 0.01 0.09 0.09 0.083 0.053 7.8 0.05 3.5 $ K \psi(4415) $ 

0 0.0151 0.0658 0.561 0.0418 0.213 2.99 0.2 5.9 0.65 0.114 0.012 0.54 0.053 0.197 5.19 0.015 4.58 0.75 0.179 0.0119 0.56 0.056 0.164 4.8 0.015 4.31 0.85 0.105 0.032 0.35 0.145 0.018 1.84 0.02 4.01 Table 2. Values of the parameters in Eqs. (11) and (12) for
$ D_s^+ \bar{D}^* \to K \psi(4040) $ ,$ K \psi(4160) $ , and$ K \psi(4415) $ .$ a_1 $ and$ a_2 $ are in units of millibarns;$ b_1 $ ,$ b_2 $ ,$ d_0 $ , and$ \sqrt{s_{\rm{z}}} $ are in units of GeV;$ c_1 $ and$ c_2 $ are dimensionless.Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K^\ast \psi(4040) $ 

0 0.04 0.02 0.46 0.068 0.1 0.96 0.06 5.78 0.65 0.008 0.1 0.19 0.028 0.032 0.76 0.035 4.94 0.75 0.002 0.041 0.1 0.027 0.029 0.6 0.03 4.73 0.85 0.06 0.002 0.12 0.37 0.014 1.09 0.015 3.83 0.9 0.18 0.003 0.47 0.5 0.04 2.79 0.04 3.63 0.95 0.32 0.035 0.1 0.88 0.008 1.39 0.01 3.39 $ K^\ast \psi(4160) $ 

0 0.009 0.016 0.41 0.024 0.08 0.66 0.05 5.89 0.65 0.0002 0.028 0.04 0.0041 0.07 0.73 0.07 4.93 0.75 0.001 0.0024 0.82 0.003 0.076 1.04 0.09 4.67 0.85 0.007 0.0495 3.76 0.0275 0.0027 0.65 0.01 4.07 0.9 0.015 0.0001 0.025 0.407 0.0073 0.609 0.01 3.63 0.95 0.06 0.005 0.75 0.18 0.026 2.77 0.025 3.46 $ K^\ast \psi(4415) $ 

0 0.01 0.04 0.71 0.02 0.08 0.43 0.05 6.2 0.65 0.006 0.148 0.25 0.03 0.031 0.56 0.04 5.02 0.75 0.0024 0.076 19.8 0.0235 0.0316 0.443 0.04 4.82 0.85 0.052 0.003 0.3 0.207 0.017 1.17 0.015 3.93 Table 3. The same as Table 1 except for
$ D_s^+ \bar{D}^* \to K^\ast \psi(4040) $ ,$ K^\ast \psi(4160) $ , and$ K^\ast \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K \psi(4040) $ 

0 0.018 0.074 0.589 0.097 0.252 3.05 0.25 5.49 0.65 0.08 0.003 0.34 0.9 0.031 1.38 0.03 4 0.75 0.32 0.002 0.52 3.07 0.0249 1.59 0.03 4.16 0.85 0.19 0.006 0.61 1.57 0.023 2.21 0.02 3.9 0.9 0.118 0.0009 0.559 0.89 0.0242 4 0.025 3.69 0.95 0.2 0.003 1.42 0.88 0.001 0.52 0.001 3.43 $ K \psi(4160) $ 

0 0.033 0.044 0.54 0.062 0.189 2.35 0.17 5.48 0.65 0.08 0.04 0.54 0.13 0.07 2.23 0.06 4.33 0.75 0.04 0.017 0.64 0.23 0.067 2.55 0.065 4.13 0.85 0.02 0.06 0.95 0.23 0.08 5.2 0.075 3.89 0.9 0.15 0.073 18 0.069 0.0129 1.7 0.07 3.72 0.95 0.062 0.066 18.1 0.189 0.0044 1.18 0.01 3.47 $ K \psi(4415) $ 

0 0.02 0.072 0.554 0.059 0.228 2.96 0.22 5.86 0.65 0.073 0.253 18 0.224 0.0142 0.78 0.025 4.6 0.75 0.07 0.003 0.49 0.3 0.03 1.26 0.03 3.94 0.85 0.078 0.009 0.27 0.301 0.05 5.6 0.05 4.03 Table 4. The same as Table 2 except for
$ D_s^{\ast +}\bar{D} \to K \psi(4040) $ ,$ K \psi(4160) $ , and$ K \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K^\ast \psi(4040) $ 

0 0.005 0.17 0.47 0.099 0.06 0.5 0.06 5.81 0.65 0.003 0.026 0.03 0.05 0.034 0.57 0.04 4.93 0.75 0.034 0.01 0.54 0.043 0.03 0.46 0.015 4.63 0.85 0.2 0.03 0.33 0.41 0.04 4.79 0.04 3.85 0.9 0.145 0.0001 0.05 2.63 0.0074 0.71 0.01 3.63 0.95 0.128 0.0001 0.041 2.08 0.0085 0.63 0.01 3.4 $ K^\ast \psi(4160) $ 

0 0.01 0.19 2.03 0.03 0.04 0.5 0.05 5.91 0.65 0.001 0.044 0.33 0.004 0.108 1.12 0.1 4.98 0.75 0.0049 0.0424 0.573 0.00193 0.175 4.08 0.04 4.68 0.85 0.07 0.001 0.03 0.28 0.01 1.44 0.01 3.92 0.9 0.03 0.003 0.19 0.25 0.02 1.67 0.02 3.73 0.95 0.004 0.006 0.94 0.05 0.034 3.36 0.035 3.58 $ K^\ast \psi(4415) $ 

0 0.018 0.13 0.8 0.021 0.03 0.48 0.05 6.3 0.65 0.004 0.008 0.35 0.053 0.037 0.51 0.04 5.01 0.75 0.016 0.011 0.84 0.045 0.027 0.39 0.02 4.74 0.85 0.07 0.007 0.79 0.33 0.04 2.71 0.04 3.94 Table 5. The same as Table 1 except for
$ D_s^{\ast +} \bar{D} \to K^\ast \psi(4040) $ ,$ K^\ast \psi(4160) $ , and$ K^\ast \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K \psi(4040) $ 

0 0.011 0.053 0.56 0.031 0.321 5.24 0.31 5.51 0.65 0.011 0.00112 0.54 0.233 0.0439 3.73 0.04 4.43 0.75 0.01 0.014 0.87 0.26 0.03 2.26 0.03 4.23 0.85 0.016 0.059 0.4 0.063 0.024 3.6 0.02 3.94 0.9 0.037 0.003 1 0.099 0.001 0.499 0.001 3.67 0.95 0.128 0.03 15 0.79 0.00135 0.75 0.001 3.36 $ K \psi(4160) $ 

0 0.002 0.006 0.395 0.027 0.148 1.19 0.19 5.59 0.65 0.0015 0.008 0.55 0.0849 0.109 6.1 0.1 4.67 0.75 0.0008 0.0054 0.496 0.0679 0.0852 5.3 0.08 4.47 0.85 0.0062 0.097 1.66 0.0027 0.0089 0.962 0.07 4.21 0.9 0.0024 0.025 0.46 0.063 0.013 2.92 0.01 3.8 0.95 0.002 0.0008 0.142 0.078 0.0125 3.55 0.01 3.41 $ K \psi(4415) $ 

0 0.0027 0.055 0.59 0.0218 0.24 2.8 0.24 5.94 0.65 0.044 0.0052 0.625 0.223 0.088 10.5 0.09 4.54 0.75 0.195 0.0727 8.79 0.0156 0.00282 0.603 0.07 4.34 0.85 0.052 0.001 1.27 0.111 0.002 0.32 0.001 3.98 Table 6. The same as Table 2 except for
$ D_s^{\ast +}\bar{D}^\ast \to K \psi(4040) $ ,$ K \psi(4160) $ , and$ K \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ K^\ast \psi(4040) $ 

0 0.051 0.015 0.43 0.138 0.09 0.93 0.07 5.71 0.65 0.0001 0.002 0.002 0.305 0.021 0.5 0.02 4.63 0.75 0.05 0.002 0.29 0.7 0.028 1.27 0.03 4.19 0.85 0.49 0.03 0.04 2.53 0.01 1.57 0.01 3.83 0.9 0.01 0.001 0.01 3.24 0.007 0.48 0.01 3.62 0.95 0.16 0.02 0.95 2.98 0.006 0.43 0.01 3.37 $ K^\ast \psi(4160) $ 

0 0.01 0.03 0.47 0.05 0.06 0.5 0.05 5.81 0.65 0.0056 0.003 0.51 0.0178 0.108 1.7 0.1 4.84 0.75 0.025 0.096 3.74 0.094 0.0042 0.57 0.01 4.46 0.85 0.041 0.001 0.05 0.361 0.016 1.51 0.015 3.96 0.9 0.014 0.012 0.71 0.037 0.031 3.72 0.03 3.84 0.95 0.00234 0.22 0.23 0.00522 0.0336 3.79 0.04 3.67 $ K^\ast \psi(4415) $ 

0 0.01 0.11 0.63 0.05 0.05 0.49 0.05 6.13 0.65 0.04 0.04 0.2 0.19 0.023 0.67 0.02 4.75 0.75 0.12 0.008 0.48 0.37 0.034 1.61 0.03 4.3 0.85 0.25 0.065 6.2 0.42 0.009 0.59 0.01 3.95 Table 7. The same as Table 1 except for
$ D_s^{\ast +} \bar{D}^\ast \to K^\ast \psi(4040) $ ,$ K^\ast \psi(4160) $ , and$ K^\ast \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ \eta \psi(4040) $ 

0 0.009 0.113 0.59 0.037 0.285 4.7 0.31 5.46 0.65 0.14 0.009 0.55 0.8 0.037 1.66 0.03 4.44 0.75 0.3 0.011 0.53 0.54 0.03 1.73 0.03 4.29 0.85 0.19 0.009 0.53 0.23 0.023 1.61 0.01 4.07 0.9 0.032 0.099 0.25 0.109 0.014 0.93 0.01 3.9 0.95 0.03 0.04 0.6 0.022 0.012 2.82 0.02 3.75 $ \eta \psi(4160) $ 

0 0.012 0.053 0.54 0.024 0.205 2.71 0.19 5.62 0.65 0.03 0.057 0.58 0.07 0.078 2.69 0.075 4.48 0.75 0.0014 0.057 0.55 0.19 0.088 3.33 0.09 4.26 0.85 0.001 0.23 0.44 0.064 0.068 3.9 0.05 4.19 0.9 0.00023 0.0024 0.57 0.0278 0.0551 5.04 0.05 3.86 0.95 0.00028 0.0044 0.695 0.0162 0.0529 7.1 0.05 3.62 $ \eta \psi(4415) $ 

0 0.0053 0.065 0.58 0.0242 0.24 3.28 0.27 5.86 0.65 0.038 0.271 21.3 0.117 0.0188 0.7 0.035 4.64 0.75 0.07 0.026 0.26 0.15 0.055 3.68 0.05 4.41 0.85 0.08 0.022 0.55 0.17 0.047 3.69 0.05 4.17 Table 8. The same as Table 2 except for
$ D_s^+ D_s^{\ast -} \to \eta \psi(4040) $ ,$ \eta \psi(4160) $ , and$ \eta \psi(4415) $ .Final state $ T/T_{\rm{c}} $ 

$ a_1 $ 

$ b_1 $ 

$ c_1 $ 

$ a_2 $ 

$ b_2 $ 

$ c_2 $ 

$ d_0 $ 

$ \sqrt{s_{\rm{z}}} $ 

$ \eta \psi(4040) $ 

0 0.0097 0.042 0.58 0.0197 0.365 7.7 0.37 5.5 0.65 0.016 0.245 16.1 0.0343 0.026 1.33 0.03 4.63 0.75 0.055 0.0154 0.81 0.025 0.201 27 0.03 4.45 0.85 0.0118 0.011 0.69 0.0064 0.16 6.9 0.01 4.42 0.9 0.00076 0.026 0.75 0.00145 0.139 3.9 0.1 4.42 0.95 0.0007 0.004 0.39 0.0009 0.083 1.58 0.1 4.21 $ \eta \psi(4160) $ 

0 0.005 0.1 0.55 0.0105 0.229 3.25 0.22 5.64 0.65 0.0046 0.842 0.496 0.0259 0.103 4.15 0.1 4.86 0.75 0.003 0.147 0.52 0.018 0.079 3.46 0.07 4.71 0.85 0.002 0.128 0.56 0.003 0.075 3.24 0.05 4.52 0.9 0.0003 0.4 0.5 0.0009 0.106 1.9 0.1 4.33 0.95 0.00002 0.002 0.33 0.000475 0.132 1.3 0.15 4.08 $ \eta \psi(4415) $ 

0 0.002 0.14 0.61 0.0101 0.29 4.26 0.33 5.92 0.65 0.042 0.08 11.7 0.03 0.31 15.9 0.08 4.77 0.75 0.025 0.275 18.9 0.032 0.059 7.4 0.06 4.6 0.85 0.0052 0.227 13.3 0.0033 0.036 0.82 0.04 4.64 Table 9. The same as Table 2 except for
$ D_s^{\ast +} D_s^{\ast -} \to \eta \psi(4040) $ ,$ \eta \psi(4160) $ , and$ \eta \psi(4415) $ .The expression on the right-hand side of Eq. (11) equals 0 at
$ \sqrt{s} = \sqrt{s_0} $ ; thus, it can be used to parametrize numerical cross sections for endothermic reactions. We denote the spins of mesons$ c\bar{q}_2 $ ,$ q_1\bar{c} $ ,$ q_1\bar{q}_2 $ , and$ c\bar{c} $ by$ S_{c\bar{q}_2} $ ,$ S_{q_1\bar{c}} $ ,$ S_{q_1\bar{q}_2} $ , and$ S_{c\bar{c}} $ , respectively. If the reaction$ c\bar{q}_2 + q_1\bar{c} \to q_1\bar{q}_2 + c\bar{c} $ is exothermic, its cross section can be related to the endothermic reaction$ q_1\bar{q}_2 + c\bar{c} \to c\bar{q}_2 + q_1\bar{c} $ using the detailed balance$ \begin{aligned} \sigma_{c\bar{q}_2 + q_1\bar{c} \to q_1\bar{q}_2 + c\bar{c}}^{\rm{unpol}} = \frac{(2S_{q_1\bar{q}_2}+1)(2S_{c\bar{c}}+1)} {(2S_{c\bar{q}_2}+1)(2S_{q_1\bar c}+1)} \frac{\vec{P}^{\prime\; 2}}{\vec{P}^2} \sigma_{q_1\bar{q}_2 + c\bar{c} \to c\bar{q}_2 + q_1\bar{c}}^{\rm{unpol}} . \end{aligned} $

(13) Hence, the expression on the right-hand side of Eq. (12) has the factor
$ \vec{P}^{\prime\; 2} / \vec{P}^2 $ .We study the production of
$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons in central Pb-Pb collisions at the LHC. Hadronic matter produced in the collisions exhibits cylindrical symmetry, and the hydrodynamic equation is solved in terms of the cylindrical polar coordinates (r, ϕ, z) [20], where the z-axis in the rest frame of hadronic matter is set along the moving direction of a nucleus and passes through the nuclear center, r is the distance from the fluid-element center to the z-axis, and ϕ is the azimuth. With the shear viscosity given in Ref. [22], the hydrodynamic equation provides the temperature and transverse velocity of hadronic matter that expands.In the source terms of the master rate equations,
$ n_D $ ,$ n_{\bar D} $ ,$ n_{D^*} $ ,$ n_{\bar{D}^*} $ ,$ n_{D_s^+} $ ,$ n_{D_s^-} $ ,$ n_{D_s^{*+}} $ , and$ n_{D_s^{*-}} $ are obtained from momentum distribution functions of charmed mesons and charmed strange mesons. Unlike pion-pion scattering, the cross sections for pion scattering by open-charm mesons are small. The thermal states of open-charm mesons may not be established by such small cross sections. We describe a Lorentz-invariant form of the momentum distribution functions of open-charm mesons:$ \begin{aligned} f_i(k_i) =\frac{1+\sum_{l=1}^{\infty} c_l (k_i\cdot u)^l}{e^{k_i\cdot u/T_{\rm{dec}}}-1}, \end{aligned} $

(14) where
$ T_{\rm{dec}} $ is the inverse slope parameter. If$\sum_{l=1}^{\infty} c_l (k_i\cdot u)^l =0$ ,$ f_i(k_i) $ becomes the Bose-Einstein distribution function. The term$ \sum_{l=1}^{\infty} c_l (k_i\cdot u)^l $ indicates deviation from thermal equilibrium. After fitting to the experimental data [61] of${\rm d}N/{\rm d}p_T$ of prompt$ D^+ $ ,$ D^0 $ ,$ D^{*+} $ , and$ D_s^+ $ mesons at$ p_T<8 $ GeV/c in central Pb-Pb collisions at$ \sqrt{s_{NN}}=5.02 $ TeV, the values of l and$ c_l $ for$ D^+ $ ,$ D^0 $ , and$ D^{*+} $ mesons are listed in Ref. [19], and those for$ D_s^+ $ mesons are listed here:$ l=15,\; \; \; \; \; c_l=6\times 10^{-17}; $

$ l \ne 15,\; \; \; \; \; c_l=0. $

$ T_{\rm{dec}} $ determined from the experimental data is 0.1686 GeV, and the value is close to the critical temperature. This means that open-charm mesons decouple early from hadronic matter. Thus, we use the momentum distribution functions (Eq. (14)) to obtain the average cross section defined in Eq. (3) for the first twenty-four terms on the right-hand side of Eq. (2). The temperature dependence of the average cross section weighted by the relative velocity results from the temperature dependence of$ \sigma_{ij \to i'j'} $ and of$ v_{ij} $ .In central Pb-Pb collisions at
$\sqrt{s_{_{NN}}}$ =5.02 TeV, hadronic matter is produced at the proper time 10.05 fm/c [19]. We start solving the hydrodynamic equation and master rate equations at the time and obtain number densities at kinetic freeze-out. Using the momentum distribution functions$1/({\rm e}^{k_i\cdot u/T}-1)$ for pions, kaons, and vector kaons in the Cooper-Frye formula [62], fitting to the experimental data of momentum spectra [23, 63], we obtain the freeze-out time of 21.07 fm/c and the freeze-out temperature of 0.126 GeV. The average cross sections in the last twenty-four terms on the right-hand side of Eq. (2) involve momentum distribution functions of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ . Currently, we assume the distribution functions have the form$\lambda_i/({\rm e}^{k_i\cdot u/T_i}-1)$ , where$ \lambda_i $ are constants and the inverse slope parameters$ T_i $ equal the dissociation temperatures of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ . We need not know the values of$ \lambda_i $ because$ \lambda_i $ in the numerator and denominator in Eq. (3) cancel each other out. The variation in the number densities with respect to the proper time ($ \tau $ ) at$ r=0 $ fm is plotted as upper solid, upper dashed, and upper dotted curves in Fig. 28, and the r dependence of the number densities at kinetic freeze-out is plotted as upper solid, upper dashed, and upper dotted curves in Fig. 29. The number densities of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons were obtained with an early version of FORTRAN code that numerically solves the master rate equations in Ref. [19]. After several errors are removed, a new version is used to calculate the number densities, which are smaller than those in Ref. [19]. When the proper time increases from 10.83 fm/c, 11.38 fm/c, and 13.95 fm/c, respectively, the number densities of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ increase. However, the three mesons produced at$ r=0 $ fm spread out, and this reduces the number densities. When the reduced amount exceeds the increased amount, the number densities decrease as shown in Fig. 28.
Figure 28. (color online) Number densities as functions of
$ \tau $ at$ r=0 $ fm. The upper solid, upper dashed, and upper dotted curves result from reactions between two open-charm mesons and their reverse reactions, and the lower solid, lower dashed, and lower dotted curves result from reactions between two charmed mesons and their reverse reactions.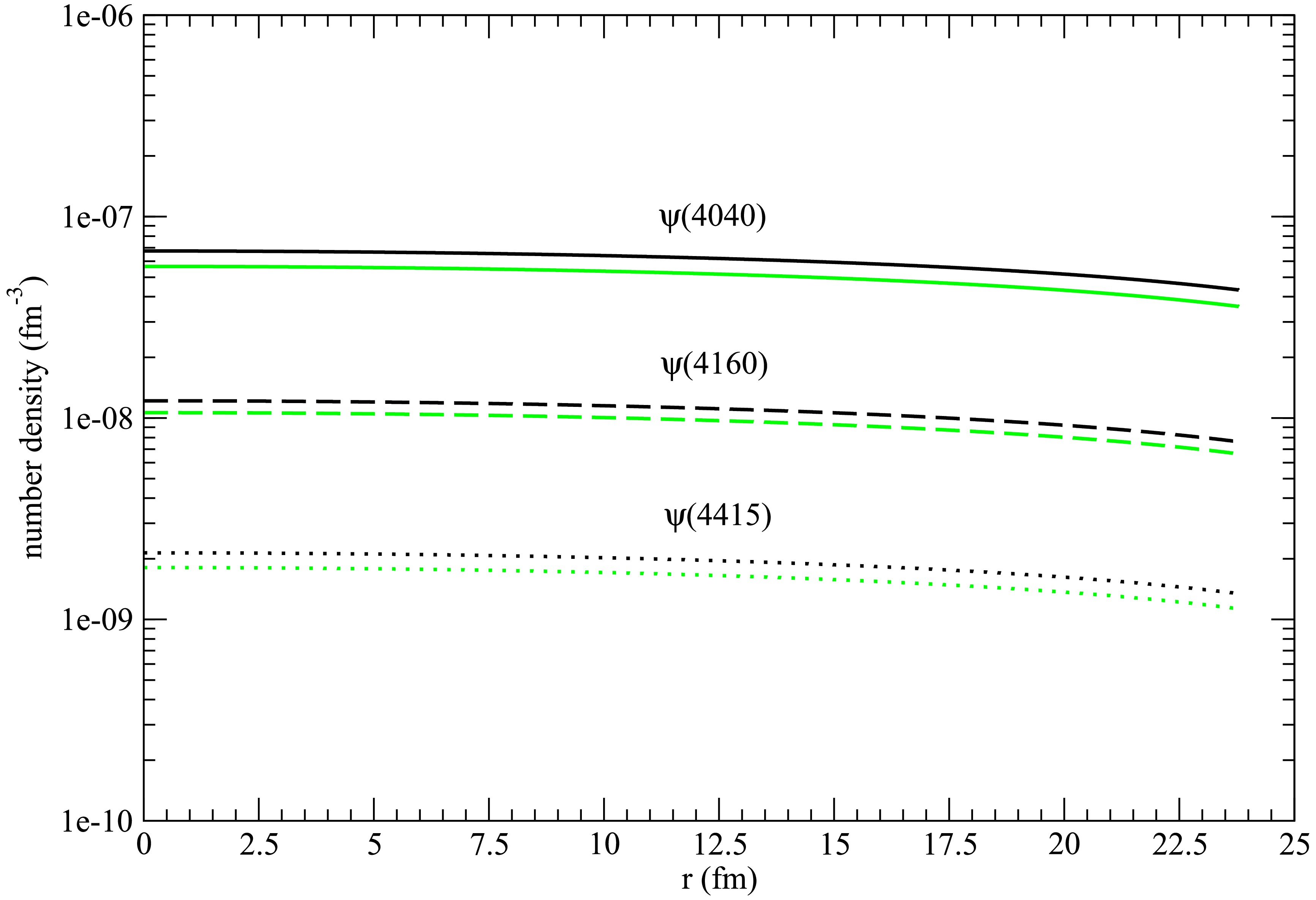
Figure 29. (color online) The same as Fig. 28, but for r dependence at kinetic freeze-out.
The upper solid, upper dashed, and upper dotted curves shown in Figs. 28 and 29 result from reactions between two charmed mesons, between a charmed meson and charmed strange meson, and between two charmed strange mesons as well as their reverse reactions. To show contributions of charmed strange mesons in producing
$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons, we plot lower solid, lower dashed, and lower dotted curves that only result from reactions between two charmed mesons. From the lower curves to the upper curves, changes in the number densities are apparent. For example, the number densities of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ at kinetic freeze-out at$ r=0 $ increase by 19.2%, 14.5%, and 18.4%, respectively, owing to the reactions of charmed strange mesons.The potential given in Eq. (10) exhibits explicit dependence on temperature. The Schrödinger equation with the potential gives temperature dependence of meson masses and mesonic quark-antiquark relative-motion wave functions. Because
$ \sqrt{s_0} $ ,$ \sqrt s $ ,$ \mid \vec{P} \mid $ , and$ \mid \vec{P}^\prime \mid $ relate to the meson masses, they depend on temperature. Consequently, the cross sections for the production of$ \psi (4040) $ ,$ \psi (4160) $ , and$ \psi (4415) $ mesons depend on temperature, as shown in Figs. 1−27. When hadronic matter expands, contributions of the twenty-seven reactions to the charmonium production differ according to the temperature. This may also be understood from the maximum of the five peak cross sections of an endothermic reaction, which correspond to the temperatures$ 0.65T_{\rm{c}} $ ,$ 0.75T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ,$ 0.9T_{\rm{c}} $ , and$ 0.95T_{\rm{c}} $ . For example, the largest peak cross section of$ D_s^+ \bar{D} \to K^\ast \psi (4160) $ ($ D_s^+ \bar{D}^\ast \to K \psi (4160) $ ,$ D_s^+ \bar{D}^\ast \to K^\ast \psi (4160) $ ,$D_s^{*+} \bar{D} \to K^\ast \psi (4160)$ ,$ D_s^{*+} \bar{D}^\ast \to K^\ast \psi (4160) $ ) appears at the temperature$ 0.95T_{\rm{c}} $ ($ 0.75T_{\rm{c}} $ ,$ 0.9T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ). Thus, the endothermic reaction$ D_s^+ \bar{D} \to K^\ast \psi (4160) $ ($ D_s^+ \bar{D}^\ast \to K \psi (4160) $ ,$ D_s^+ \bar{D}^\ast \to K^\ast \psi (4160) $ ,$ D_s^{*+} \bar{D} \to K^\ast \psi (4160) $ ,$D_s^{*+} \bar{D}^\ast \to K^\ast \psi (4160)$ ) may produce the largest amount of$ \psi (4160) $ mesons at$ 0.95T_{\rm{c}} $ ($ 0.75T_{\rm{c}} $ ,$ 0.9T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ,$ 0.85T_{\rm{c}} $ ) during the evolution of hadronic matter.The temperature dependence of the interquark potential has been obtained in the lattice gauge calculations. The potential shows that the interaction range decreases sharply around the critical temperature [64]. Consequently, the
$ c\bar c $ relative-motion wave functions obtained from the Schrödinger equation with the potential show that the spatial size of each wave function increases rapidly when the temperature increases from a cetain value. This value is near the critical temperature and depends on the quantum numbers of$ c\bar c $ states. Thus, we take this value as the dissociation temperature of the$ c\bar c $ state. This method is valid not only for bound states such as$ J/\psi $ ,$ \chi_c $ , and$ \psi^\prime $ but also for resonances such as$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ .The number densities obtained from the master rate equations depend on the average cross sections weighted by the relative velocity and dissociation temperatures of
$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons. The averages$ \langle \sigma_{ij\to i^\prime \psi(4040)} v_{ij}\rangle $ and$ \langle \sigma_{ij\to i^\prime \psi(4415)} v_{ij}\rangle $ are typically 5 and 3.3 times$ \langle \sigma_{ij\to i^\prime \psi(4160)} v_{ij}\rangle $ , respectively. In addition, the dissociation temperature of$ \psi(4040) $ is higher than that of$ \psi(4160) $ . Hadronic matter requires a long time to produce$ \psi(4040) $ than to produce$ \psi(4160) $ . Thus, we observe that the number density of$ \psi(4040) $ is larger than that of$ \psi(4160) $ in Figs. 28 and 29. However, because the dissociation temperature of$ \psi(4415) $ is lower than that of$ \psi(4160) $ , hadronic matter requires a short time to produce$ \psi(4415) $ than to produce$ \psi(4160) $ . This factor causes the number density of$ \psi(4415) $ to be smaller than that of$ \psi(4160) $ . The number densities and volume of hadronic matter at kinetic freeze-out yield 0.0034, 0.0006, and 0.00011 as the numbers of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons produced in a central Pb-Pb collision at$\sqrt{s_{_{NN}}}=5.02$ TeV, respectively.The first twenty-four terms on the right-hand side of Eq. (2) are gain terms of producing
$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons, and the other terms are loss terms of breaking the three charmonia. The cross sections for$ q_1\bar{q}_2 + c\bar{c} \to c\bar{q}_2 + q_1\bar{c} $ in the loss terms are obtained from those for$ c\bar{q}_2 + q_1\bar{c} \to q_1\bar{q}_2 + c\bar{c} $ using detailed balance. The inclusion of the loss terms in the master rate equations reduces the number densities of the charmonia, but the difference between the number densities obtained from Eq. (1) with the loss terms and without the loss terms is small. For example, the number density of$ \psi(4040) $ ($ \psi(4160) $ ,$ \psi(4415) $ ) at$ r=0 $ fm at kinetic freeze-out is$ 6.75 \times 10^{-8} $ $ {\rm{fm}}^{-3} $ ($ 1.22 \times 10^{-8} $ $ {\rm{fm}}^{-3} $ ,$ 2.14 \times 10^{-9} $ $ {\rm{fm}}^{-3} $ ) with the loss terms and$ 7.35 \times 10^{-8} $ $ {\rm{fm}}^{-3} $ ($ 1.25 \times 10^{-8} $ $ {\rm{fm}}^{-3} $ ,$ 2.21 \times 10^{-9} $ $ {\rm{fm}}^{-3} $ ) without the loss terms. The reason for the small difference is that the number densities of the charmonia are small. The maximum number densities appear at$ r=0 $ fm. The upper solid, upper dashed, and upper dotted curves in Fig. 28 show that the maximum number densities of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ are$ 1.95 \times 10^{-7} $ $ \rm{fm}^{-3} $ ,$ 3.05 \times 10^{-8} $ $ \rm{fm}^{-3} $ , and$ 3.49 \times 10^{-9} $ $ \rm{fm}^{-3} $ , respectively. The number densities of pions, kaons, η mesons, ρ mesons, and vector kaons are obtained from the Bose-Einstein distribution. The product of the number densities of the charmonia and light-quark mesons yields small loss terms that cause the small difference. -
We have studied the production of
$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ mesons in ultrarelativistic heavy-ion collisions at the LHC. This research includes two parts. In the first part, we have studied the charmonium production from the reactions between charmed strange and open-charm mesons. These reactions result from the quark interchange in association with color interactions between all constituent pairs in different mesons. Fifty-one reactions are considered, and we have presented numerical unpolarized cross sections and their parametrizations for twenty-seven reactions:$ D_s^+ \bar{D} \to K^\ast R $ ,$ D_s^+ \bar{D}^\ast \to K R $ ,$ D_s^+ \bar{D}^\ast \to K^\ast R $ ,$ D_s^{\ast +} \bar{D} \to K R $ ,$ D_s^{\ast +} \bar{D} \to K^\ast R $ ,$ D_s^{\ast +} \bar{D}^\ast \to K R $ ,$ D_s^{\ast +} \bar{D}^\ast \to K^\ast R $ ,$ D_s^+ D_s^{\ast -} \to \eta R $ , and$ D_s^{\ast +} D_s^{\ast -} \to \eta R $ , where R indicates$ \psi(4040) $ ,$ \psi(4160) $ , or$ \psi(4415) $ . We have presented characteristics of the endothermic reactions below the critical temperature and of the reactions that are endothermic at some temperatures and exothermic at others. The characteristics are related to confinement, mesonic quark-antiquark relative-motion wave functions, and$ \mid \vec{P}^{\; \prime} \mid / \mid \vec{P} \mid $ . In the second part, we have studied the production of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ in hadronic matter that results from the quark-gluon plasma created in Pb-Pb collisions at the LHC. We have established the master rate equations with the new source terms that include the reactions between charmed strange and open-charm mesons and their reverse reactions. The temperature dependence of the cross sections reflects different contributions of the fifty-one reactions to the charmonium production at different temperatures. The master rate equations in association with the hydrodynamic equation are solved to obtain number densities of$ \psi(4040) $ ,$ \psi(4160) $ , and$ \psi(4415) $ . In central Pb-Pb collisions at$\sqrt{s_{_{NN}}}=5.02$ TeV, the number density of$ \psi(4040) $ is larger than that of$ \psi(4160) $ , whose is larger than that of$ \psi(4415) $ . The reactions between charmed strange and open-charm mesons increase the number densities. The small number densities cause the loss terms to be small. -
We thank Prof. H. J. Weber for careful readings of the manuscript.
Production of $ {{\boldsymbol\psi} {\bf{ (4040)}}} $ , ${ \boldsymbol\psi \bf (4160) }$ , and ${ \boldsymbol\psi \bf (4415) }$ mesons in strong interactions
- Received Date: 2024-04-12
- Available Online: 2025-02-15
Abstract: Using the inelastic scattering of charmed strange mesons by open-charm mesons in hadronic matter produced in Pb-Pb collisions at the Large Hadron Collider, we study the production of


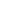
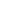
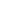



 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: