Systematic research on the ground state properties of medium-mass neutron-rich nuclei

The planning, construction, and upgrading of large-scale radioactive nuclear beam devices worldwide have extended the study of atomic nuclei from stable to exotic nuclei far from the β-stability line. Research on exotic nuclei is one of the most prominent and challenging frontier topics in nuclear physics, both experimentally [1−4] and theoretically [5−10]. Many interesting phenomena have been observed in weakly bound nuclei, especially in those with extreme $N/Z$ratios, including the neutron (proton) halo, change in magic numbers, and pygmy resonances. Through exotic nuclei research, we can understand the nuclear structure as well as element synthesis and astrophysics. However, the extremely short lifetime and small formation cross-section of exotic nuclei pose several experimental challenges. Therefore, theoretical studies on exotic nuclei are important for experimental exploration and the analysis of experimental data.

Because the Fermi surfaces of weakly bound nuclei are very close to the continuum threshold, the valence nucleons in these nuclei are easily scattered into the continuum due to the pairings, resulting in nuclear density distribution diffusion. The continuum, especially resonant states in the continuum, plays a crucial role in the formation of these exotic phenomena. Therefore, it is essential to properly treat the resonant states, especially those close to the threshold, in the continuum and pairings in theoretical research on exotic nuclei [11−14].

Physicists have developed many models for pairings and resonances in exotic phenomena due to their importance. The traditional BCS theory is considered unreliable for nuclei near the drip line due to the improper treatment of the continuum [15, 16]. However, if physical resonant states can be obtained rather than a non-physical continuum, the BCS is valid. The earliest study in this direction is reported in Ref. [17], wherein the BCS equations were extended to incorporate the contribution of the resonant states through the generalized level density, and the resonant continuum was shown to have an important effect on neutron-rich nuclei.

The BCS approximation and complex scaling method (CSM) were introduced in the Hartree-Fock calculation, and the exotic structures of these nuclei were studied in the proton drip-line region around the double magic nucleus ⁴⁸Ni [18]. Based on the Berggren representation, the BCS approximation was used to treat pairings in the Hartree-Fock calculation, and $^{10-22}$O and $^{84}$Ni were well studied [19]. The Berggren representation has also been used to explore quasiparticle resonances with BCS approximation for pairings [20]. Green’s function method [21, 22] has been demonstrated to be an efficient tool for describing single-particle resonant states. The giant halos predicted in the neutron-rich Zr isotopes were reproduced in Skyrme-Hartree-Fock-Bogoliubov calculations [23], where the asymptotic behavior of continuum quasiparticle states was properly treated by the Green's function method. In 2010, the coupling channel method was used to calculate single-particle resonances and reveal the physical mechanism of $^{31}$Ne halos [24]. Recently, this method was used to predict neutron halo nuclei heavier than $^{37}$Mg [25].

Relativistic mean-field (RMF) theory is one of the most successful microscopic theoretical models and has been quite successful in describing nuclear properties. Together with the radial basis function or neural network approach, the accuracy of its mass predictions can even be similar to that of sophisticated macro-microscopic mass models [26−28]. To account for the contribution of resonances, RMF theory has been combined with the analytical continuation of coupled constant (ACCC) approach [29], real stabilization method (RSM) [30], and CSM [31−33] for resonances. The developed RMF-ACCC [34, 35], RMF-RSM [36], and RMF-CSM [37−39] methods provide excellent descriptions of the ground state properties for the weakly bound nuclei. The continuum relativistic Hartree-Bogoliubov (RHB) theory [40] presents a satisfactory description of halos in $^{11}$Li and a prediction of giant halos in Zr and Ca isotopes [41, 42]. The Green's function method has also been used to explore the bound and unbound states in the RMF framework [43].

Although these methods have been successfully used to investigate resonant states, obtaining broad resonances near the continuum threshold is not easy. The bound and resonant states are obtained by solving the equation of motion in a complex momentum space. Accordingly, the complex momentum representation (CMR) method was proposed for resonances [44]. It has been shown that the CMR method can describe the bound states, resonances, and continuum and does not miss the broad resonant states with lower orbital angular momentum near the threshold. The broad resonances with lower orbital angular momentum near the threshold play a crucial role in the formation of exotic phenomena. This allows us to accurately describe the ground state properties of $^{120}$Sn [44] and the physical mechanism of deformation halo in $^{37}$Mg [45]. Meanwhile, the BCS approximation is used to treat the pairing correlations between the bound and resonant states in a continuous spectrum, which can well describe exotic phenomena such as halos and giant halos [46−49].

One of the most interesting nuclide regions is located between $Z=35-64$ and $A=82-132$. This region reveals many interesting exotic phenomena, such as halos and change in magic numbers. In particular, neutron-rich nuclei near the double magic nucleus $^{132}$Sn have attracted significant attention. Although $^{132}$Sn exhibits the typical characteristics of a double magic nucleus, the persistence of magic number $N=82$ has been questioned in many theoretical studies [50, 51]. Over the past $30$ years, previous studies have shown that some magic numbers have disappeared in certain neutron-rich regions, while new ones may appear. That is, magic numbers are not universally mandatory [52−54]. Moreover, possible giant halos were predicted in extremely neutron-rich Zr and Sn isotopes [9, 46, 14]. However, the nuclear structure information around $Z=50$ is not rich in experimental data because it is difficult to generate; thus, this is an active field of experimental and theoretical research [41, 55, 56].

Research on the nuclear structures near $Z=50$ has mainly focused on the $N=82$ region [57−77]. Refs. [57, 58, 76, 77] give the calculation results of physical quantities such as two-neutron separation energy for Pd isotopes. Ref. [59] studied the neutron-rich $^{122,124,126}$Pd isotope, indicating the existence of the magic number $N=82$. Boelaert et al. calculated the shell model of neutron-deficient Cd nuclei from $N=50$ to $N=58$ [61]. In particular, the $^{136}$Te isotope with one proton and one neutron pair outside the robust double magic $^{132}$Sn core has attracted much attention from nuclear physicists for a long time [66, 69, 71]. However, studies on other exotic phenomena, such as magic numbers and halos, in Pd, Cd, Te, and Xe isotopes, are relatively scarce. To further clarify the exotic structures of these nuclei, it is necessary to explore their ground state properties, especially their single-particle level structures. Given the advantages of the RMF+CMR+BCS method in dealing with single-particle resonant states and its success in studying exotic nuclei, it is considered a powerful tool to further study the nuclear properties near $Z=50$. To the best of our knowledge, this is the first systematic study of shell structures and exotic properties in nuclei within the $Z=50$ region.

In this study, we applied the newly developed RMF+CMR+BCS method to properly treat the pairings and couplings with the continuum and to systematically study the exotic properties of the even-even Pd, Cd, Te, and Xe isotopes. The remainder of this paper is organized as follows. The theoretical formalism is described in Section II. The numerical details are presented in Section III. The results and discussion are given in Section IV. Finally, Section V summarizes the study and its findings.

To explore the effects of single-particle resonant states and pairing correlations on the exotic structures and properties of the medium-mass even-even nuclei, we developed the RMF+CMR+BCS method by combining the RMF theory and CMR method and using the BCS approximation to couple bound and physical resonant states. First, let us briefly describe the theoretical framework of the RMF+CMR+BCS method. The Lagrange density can be written as [78]

where ψ and m denote the Dirac spinor and nucleon mass, respectively. σ, $\omega ^{\mu }$, and $\boldsymbol{\rho}^{\mu }$ are the isoscalar-scalar, isoscalar-vector, and isovector-vector meson fields, respectively. $g_{\sigma }$, $g_{\omega }$, and $g_{\rho }$ are coupling constants. $A^{\mu }$ is the photon field. The field tensors are defined as follows:

Based on the Lagrange density, we can obtain the RMF theory equations. More details can be found in the literature [9, 78, 79]. For a static nucleus, the RMF theory equations are simplified to the Dirac equation as follows:

The scalar and vector potentials of the nucleus are expressed as

and the Klein-Gordon equations as

The meson and photon densities are respectively expressed as

For spherical nuclei, the Dirac spinor can be written as

The radial density distributions are obtained as follows:

Because the expressions for $\rho_{3}$ and $\rho_{c}$are the same as those for $\rho_{v}$ except that the sum of the levels considered is different, they are ignored here. Eqs. (3) and (5) are solved iteratively with a given accuracy. In the RMF framework, the total energy of the system is obtained as follows:

A center-of-mass correction is considered as [80]

This formulation is effective for stable nuclei. For weakly bound nuclei, their Fermi surfaces are very close to the continuum threshold, and the contribution of the resonant states cannot be ignored. To include the resonant states, the Dirac equation (Eq. (3)) is transformed into the momentum representation

where $H=\boldsymbol{\alpha}\cdot \boldsymbol{p}+\beta \left( m+S\left( \boldsymbol{r}\right) \right) +V\left( \boldsymbol{r}\right)$. For spherical nuclei, assuming

the Dirac equation becomes

with

The above equations are solved in complex momentum space using the Berggren basis [81], and both the bound and resonant states are obtained. The details can be found in Ref. [44]. To obtain the density distributions in coordinate space, we transform the wavefunctions into a coordinate representation with the upper and lower components in Eq. (7) as follows:

Furthermore, it is necessary to obtain the wavefunctions to more accurately determine the existence of exotic phenomena, such as halos.

For open-shell nuclei, it is critical to consider the contribution of pairings. As resonant states are clearly separated from the continuum in the CMR calculations [44], the BCS approximation is applicable and effective for pairings [46, 47]. The matrix element of the pairing interactions is assumed to be constant near the Fermi level [80]. When the resonances are considered, the pairing correlations can be dealt with using the gap equation

and particle number equation

where G, Δ, and N denote the pairing strength, pairing energy gap, and particle number, respectively. $\Omega_{\sigma}=j_{\sigma}+\dfrac{1}{2}$ with $\sigma=b$ for bound states and $\sigma=r$ for resonant states, and

with the real part of resonance energy $\varepsilon_{r}$ and width Γ. The solutions of Eqs. (17) and (18) provide the occupation probabilities for the bound and resonant levels. For the occupations, the densities in Eq. (8) are modified to

After these modifications, the total energy of the system becomes

Compared with the relativistic HFB method [9], the advantage of the CMR method is that the physical mechanism of the halos can be revealed from the contributions of every resonant level [46, 47].

The starting point of this study was the RMF framework within the Berggren basis. This section outlines the calculation steps and numerical details of the RMF +CMR + BCS method based on the above theoretical formulation.

Similar to the traditional RMF theory, the RMF+CMR+BCS method solves the Dirac (3) and Klein-Gordon (5) equations. These coupled equations are complicated, and the density and energy can only be solved iteratively from an initial guess of the scalar potential S and vector potential V. To obtain bound and resonant states as well as the continuous spectrum on the same basis, Eq. (3) is solved by considering the momentum completion basis and transforming it into the complex momentum representation such that the Dirac equation is transformed into the complex momentum representation in Eq. (11). Substituing Eq. (12) into Eq. (11), the Dirac equation can be expressed as Eq. (13) through a series of solutions; the angular part is removed, and its solution gives single-particle energy E and the wavefunctions $f(k)$ and ${g}(k)$ of the momentum representation.

The RMF+CMR method can not only obtain bound and resonant states but also broad resonant states that are difficult to obtain using other bound-state-like methods. With these single-particle bound and resonant states, the pairings are treated using the BCS approximation by solving Eqs. (17) and (18) for a given energy gap Δ. For convenience, an empirical formula $\Delta= \delta/\sqrt{A}$ ($\delta=12$) is adopted for neutron and proton pairings [82]. The energy gap parameter δ is fixed by fitting the experimental data. The pairing window can be determined by fitting the odd-even mass differences. In this study, the pairing window is denoted as 41$A^{-1/3}$. The occupation probabilities $v^{2}$ of the bound and resonant states can be obtained by solving Eqs. (17) and (18). The obtained occupation probabilities of the single-particle levels and wavefunctions of the coordinate representation are considered in Eq. (20) to further obtain the densities $\rho_{s}$ and $\rho_{v}$. The wavefunctions $f(r)$ and ${g}(r)$ are obtained by solving Eq. (16). The obtained density and potential (V($\boldsymbol{r}$)and S($\boldsymbol{r}$)) are given by Eqs. (5) and (3), respectively, to calculate the meson field and a new set of potentials. This cycle is repeated until convergence.

In the actual calculations, the Dirac equation (Eq. (13)) is solved in complex momentum space, and as the resonant states are independent of the integration path [44], we apply momentum integration along an appropriate contour (K₁ = 0 fm⁻¹, K₂ = 0.6–0.2 fm⁻¹, K₃ = 1.0 fm⁻¹, and K₄ = 4.0 fm⁻¹, where K₁, K₂, K₃, and K₄ represent the four coordinate points of the triangular integral path of momentum space, respectively). In this study, the coordinate space has a space size of R_box = 30 fm and grid size of d_r = 0.1 fm. Finally, the effective interaction NL3^* [83] is adopted because of its improved description of the ground state properties of many nuclei.

To better understand the contributions of single-particle levels to exotic phenomena, we obtained neutron single-particle levels of even-even Pd, Cd, Te, and Xe isotopes. The neutron single-particle levels of $^{110-160}$Pd, $^{110-164}$Cd, $^{120-182}$Te, and $^{120-184}$Xe within the $-12 - +8$ MeV range are shown in Fig. 1. The bound and resonant states are marked by the solid and hollow symbols, respectively. The Fermi surface is marked by the short-dotted line. As the neutron number increases, all single-particle levels decrease, while the Fermi energy λ increases in each chain, eventually reaching the continuum threshold. In this study, the shell evolutions between single-particle levels were explored based on the average shell gap $\langle\Delta\rangle= \frac{\left(\sum_{A_{\rm min}}^{A_{\rm max}}\Delta_{N}\right)}{[(A_{\rm max}-A_{\rm min})/2]+1}$ given in Ref. [84], where $\Delta N$ is the shell gap between the levels for a given nucleus.

Figure 1.  (color online) Neutron single-particle levels as a function of mass number A obtained for the even-even Pd, Cd, Te, and Xe isotopes. The bound and resonant states are marked by the solid and hollow symbols, respectively. The Fermi surface is marked by a short-dotted line. These levels are labeled as $nl_{j}$, where n, l, and j are the radial, orbital, and total angular momentum quantum numbers, respectively.

For the Pd isotope, the levels 1i$_{13/2}$, 2g$_{9/2}$, 2g$_{7/2}$, and 1i$_{11/2}$ remain as resonant states. However, the levels 2f$_{7/2}$, 1h$_{9/2}$, and 2f$_{5/2}$ transition from resonant states to bound states with an increase in neutron number N. The average shell gaps between levels 1h$_{11/2}$ and 2f$_{7/2}$ and between 2f$_{5/2}$ (1h$_{9/2}$) and 1i$_{13/2}$ are $4.57$ MeV and $3.26$ MeV, respectively, indicating that the traditional magic number $N=82$ exists and a new magic number $N=112$ appears. Furthermore, there is no large gap between levels 1i$_{13/2}$ and 2g$_{9/2}$ (the average shell gap is only $0.89$ MeV), suggesting that the traditional magic number $N=126$ disappears on the extremely neutron-rich side. Notably, the levels 3p$_{3/2}$ and 3p$_{1/2}$ (now referred to as $3$p) appear at $A=118$ and $A=124$, respectively. The $3$p levels favor the formation of halo phenomena due to the lower orbital angular momentum. However, the 3p levels become increasingly bound as the neutron number increases, which is not conducive to halo formation and is more inclined to form a thicker neutron skin. Similar to Pd isotopes, the same phenomena were observed in Cd isotopes. Different from the Pd isotopes, the levels 3p$_{3/2}$ and 3p$_{1/2}$ appear at $A=116$ and $A=120$, respectively. For Te isotopes, the resonant levels 3d$_{5/2}$, 4s$_{1/2}$, and 1j$_{15/2}$ appear on the extremely neutron-rich side. It is worth noting that a large gap appears between weakly bound level 1i$_{13/2}$ and resonant level 2g$_{9/2}$ (3d$_{5/2}$) (the average shell gap between them is $2.46$ MeV), which means that the magic number $N=126$ does not disappear. Although the magic number $N = 126$ exists, the gap (the shell gap between the levels 1i$_{13/2}$ and 3d$_{5/2}$ at $A=178$) is approximately $2.2$ MeV, and the shell gap is weakened. From $A=164$ to $A=182$, neutrons are scattered into resonant states above the zero-potential energy level due to pairing correlations. Although the orbital angular momentum of level 4s$_{1/2}$ ($l=0$) is low, its single-particle energy reaches approximately $6$ MeV. This implies that the relative contribution of level 4s$_{1/2}$ to the neutron halo is not significant. The resonant level 3d$_{5/2}$ is occupied in favor of halo formation, which means that a neutron halo may appear from $^{164}$Te to $^{182}$Te. For the Xe isotope, the level 3d$_{3/2}$ appears on the extremely neutron-rich side. Similar to level 4s$_{1/2}$ for Te isotope, the level 3d$_{3/2}$ does not support halo formation. The large gap between levels 1i$_{13/2}$ and 3d$_{5/2}$ indicates the existence of the magic number $N=126$ (the average shell gap between them is only $3.06$ MeV). Due to the weakened energy gap and pairings, the neutrons are easily scattered into resonance levels above the zero-potential energy level at $164\leq A\leq184$. Therefore, neutron halos may appear from $^{164}$Xe to $^{184}$Xe.

On the extremely neutron-rich side of the Pd, Cd, Te, and Xe isotopes, especially in the weakly bound nuclei near the neutron drip-line, the Fermi surface is close to the continuum threshold, and valence neutrons are easily scattered into the continuum and occupy the resonant states. This indicates that the stability of these halo isotopes is highly sensitive to pairing effects.

To further explore the effect of pairings on halos, we plot the neutron number $N_{\lambda}$ and $N_{E > -2\;{\rm MeV}}$ located above the Fermi surface with single-particle energey greater than $-2$ MeV for the Pd, Cd, Te, and Xe isotopes, respectively, as shown in Fig. 2. We can observe that, on the neutron-deficient side, $N_{E > -2\;\;\rm MeV}$ is particularly close to $0$, which is due to these nucleons being deeply bound. It is noteworthy that near the magic numbers and extremely neutron-rich nuclei, $N_{\lambda}$ and $N_{E > -2\; {{\rm{MeV}}}}$ coincide. Additionally, for Te isotopes on the extremely neutron-rich side, the value of $N_{E > -2\;\;{\rm MeV}}$ is notably elevated, reaching the range of $12-18$ MeV. This is attributed to the single-particle level 1i$_{13/2}$ remaining higher than $-2$ MeV in this region.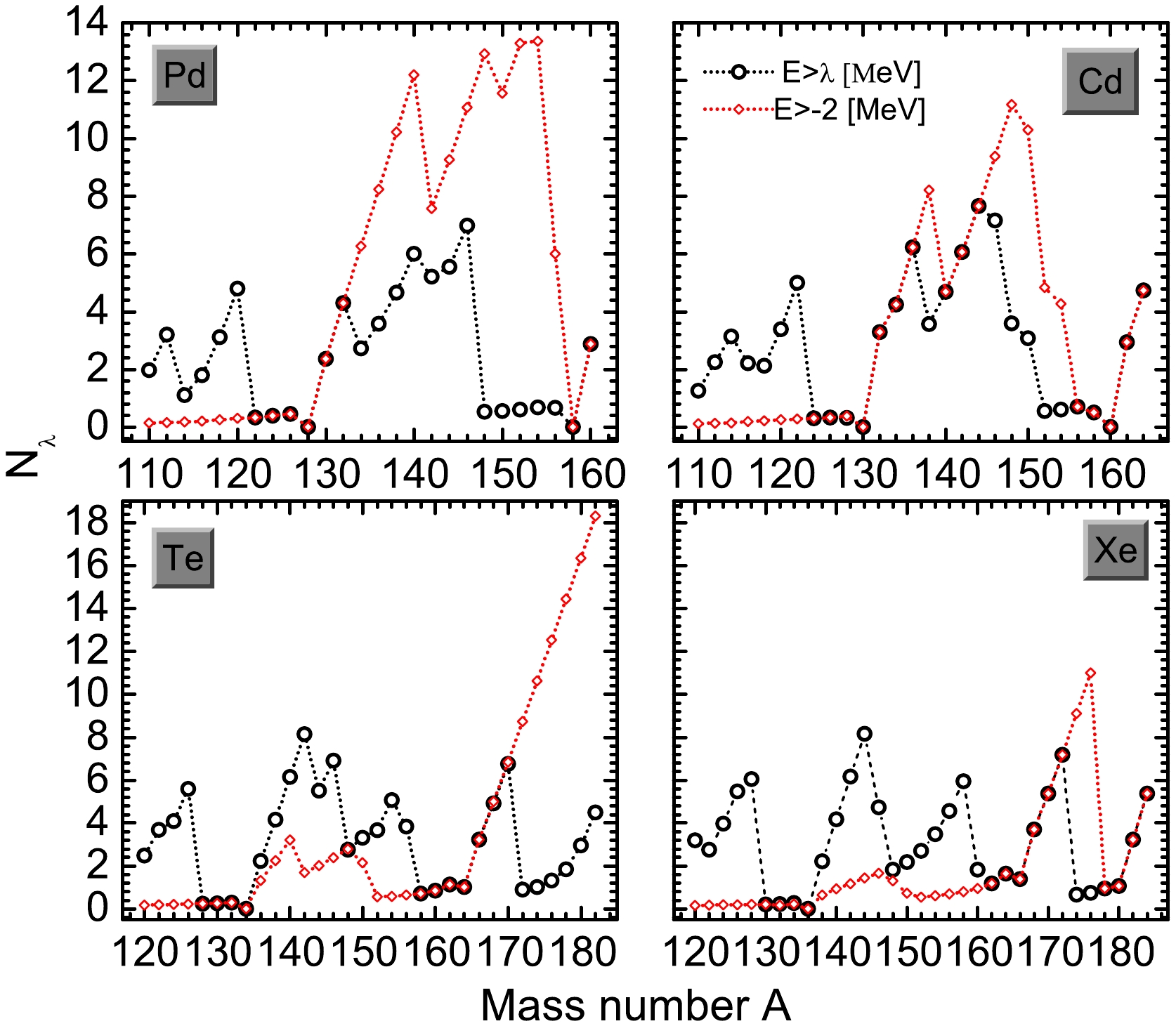

Figure 2.  (color online) Neutron numbers $N_{\lambda}$ and $N_{E > -2 \;{{\rm{MeV}}}}$, which are occupied above the Fermi surface and possess single-particle energies greater than $-2$ MeV, were obtained for the Pd, Cd, Te, and Xe isotopes, respectively.

Substantial amounts of neutrons are scattered from the single-particle levels below the Fermi surface to weakly bound or resonant states above it because of the pairing, especially in nuclei where the half-full shells are filled with neutrons. Meanwhile, obvious shell structures can be observed. Because of the absence of pairings in closed-shell nuclei, $N_{\lambda}$ approaches zero when the neutron number reaches a magic number. For Pd and Cd isotopes, $N_{\lambda}$=0 at $N=82,112$. For Te and Xe isotopes, $N_{\lambda}$=0 at $N=82$. However, very small neutron occupancies are observed at the single-particle levels above the Fermi surface ($N_{\lambda}\neq 0$) at $N = 112$ and $N = 126$, suggesting that these nuclei have weak pairings. The existence of weak pairings leads to resonant states near the zero-potential energy level being occupied, which is conducive to halo formation. The evolution of $N_{\lambda}$ and $N_{E > -2\;{\rm MeV}}$ with mass number A supports the results shown in Fig. 1.

The obtained neutron numbers $N_{0}$ above the zero-potential energy level ($E_{r}>0$ MeV) for the even-even Pd, Cd, Te, and Xe isotopes are shown in Fig. 3. $N_{0}$ is substantially reduced compared to $N_{\lambda}$. For Pd isotopes, $N_{0}$ is less than unity except for $^{132-136}$Pd and $^{160}$Pd. The larger $N_{0}$ of $^{132-134}$Pd is due to levels 1h$_{9/2}$ and 2f$_{5/2}$ being low-lying resonant states, while that of $^{136}$Pd results from the occupation of level 1i$_{13/2}$. In the neighboring $^{128}$Pd, the occupation probabilities of levels 1h$_{9/2}$ and 2f$_{5/2}$ are extremely small and almost zero. As the neutron number increases further, $N_{0}$ remains less than unity. At $^{160}$Pd, $N_{0}$ suddenly increase because resonant levels 1i$_{13/2}$, 2g$_{9/2}$, and 2g$_{7/2}$ begin to be occupied. Similar phenomena were observed in the Cd, Te, and Xe isotopes, except in the case of the Te and Xe isotopes with $N=112$ and $N=126$. The evolution of $N_{0}$ with mass number A closely resembles that of $N_{\lambda}$ and E$_{r}$ with A.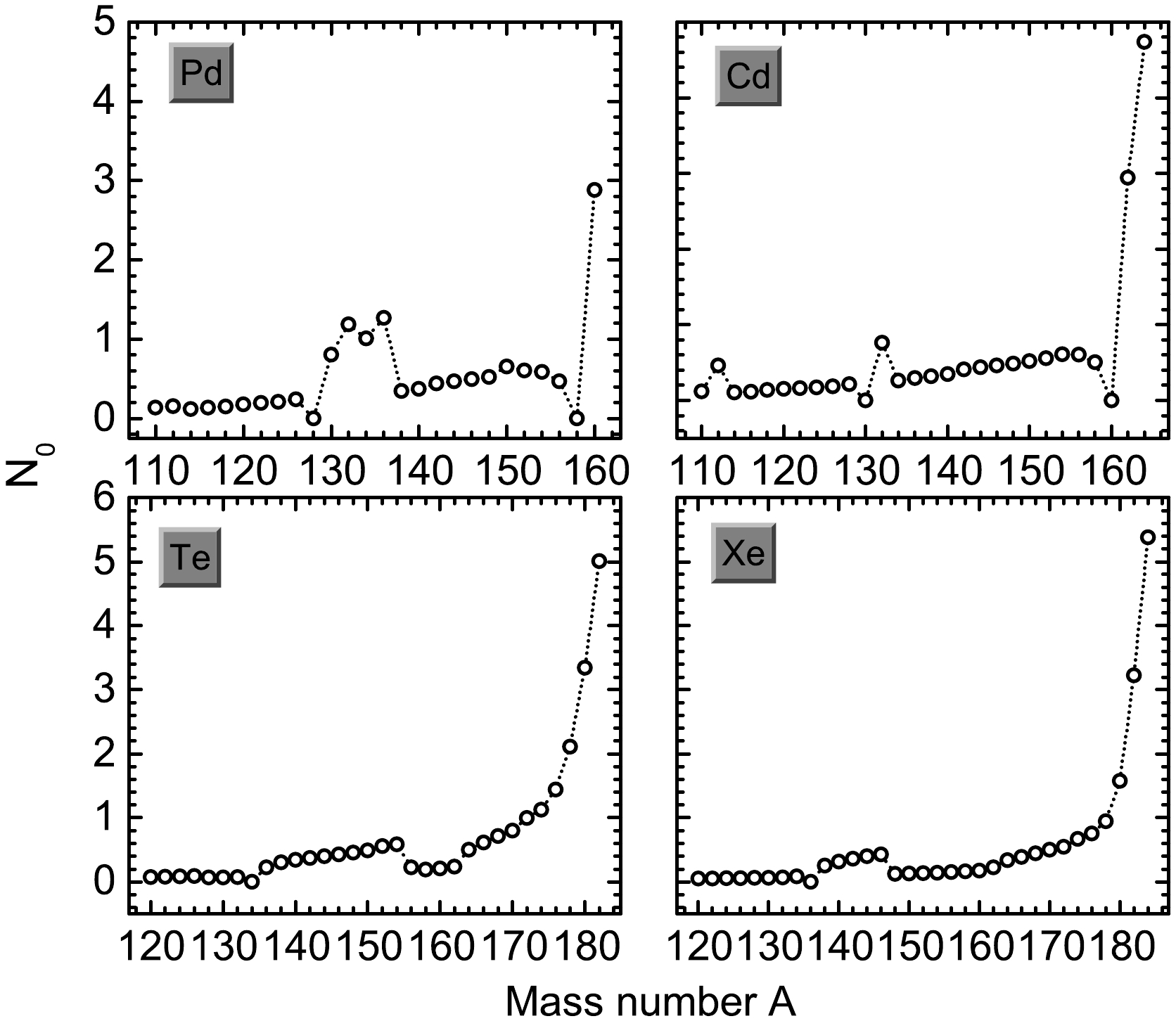

Figure 3.  (color online) Neutron numbers $N_{0}$ occupied at single-particle levels above the continuum threshold (above the zero-potential energy level $E_{r}=0$ MeV) obtained for Pd, Cd, Te, and Xe isotopes.

The two-neutron separation energy $S_{2n}$(Z, N) = B(Z, n-2)−B(Z, N) is not only a sensitive physical quantity for testing the microcosmic theory but also an important observation value for nuclear binding and exotic properties. The two-neutron separation energies of even-even Pd, Cd, Te, and Xe isotopes were calculated and compared with the results of the RMF+CMR method [44], RMF+BCS method [85], RHB method [41], and available experimental data [86], as shown in Fig. 4. Although the RMF+CMR method is suitable for describing weakly bound nuclei far away from the β-stability line, it does not consider the contribution of pairings, which neglects residual interaction between nucleons. In contrast, while the RMF+BCS method considers the contribution of pairings and solves the blocking effect caused by single-particle excitations, it does not consider the contributions from resonant states and is only valid for bound states. Therefore, it can be clearly observed that the RMF+CMR and RMF+BCS results deviate the most from the experimental data. Moreover, the RMF+BCS and RMF+CMR results are similar because the RMF+BCS approach may involve unphysical states, leading to divergence. The RMF+CMR+BCS method includes coupling between the bound and resonance states with positive energies. In general, compared with the RMF+CMR and RMF+BCS results, the RMF+CMR+BCS results are in good agreement with the RHB calculations and available experimental data. These results indicate that the RMF+CMR+BCS calculations are reliable and the neutron drip-line prediction is accurate.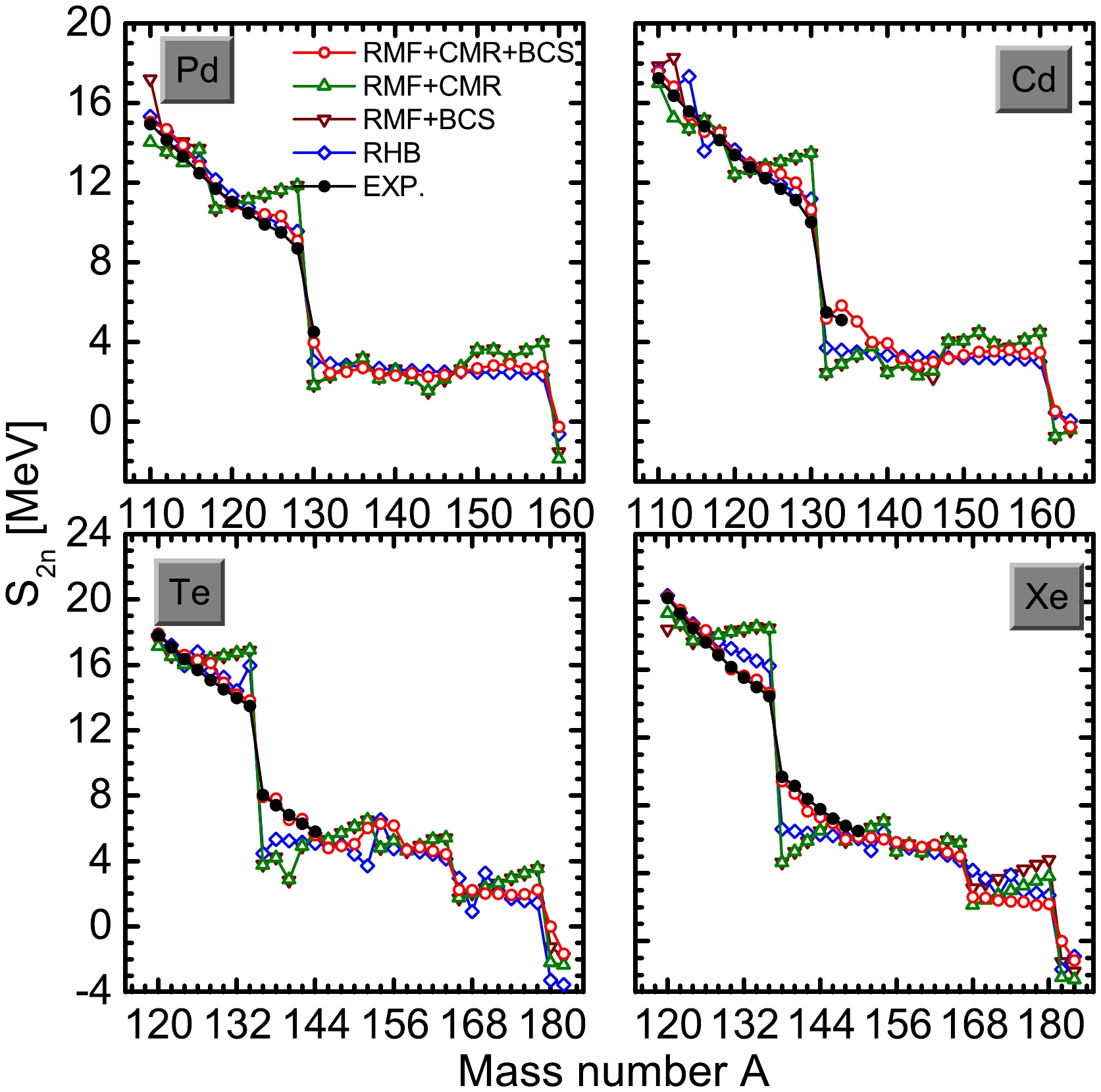

Figure 4.  (color online) Two-neutron separation energies of even-even Pd, Cd, Te, and Xe isotopes as a function of mass number A. The red open circles, green open triangles, purple open inverted triangles, and blue open diamonds correspond to the RMF+CMR+BCS, RMF+CMR, RMF+BCS, and RHB calculations, respectively. The black solid circles represent the experimental data [86].

For the Pd and Cd isotopes, there are large gaps at $N=82$ and $N=112$ that support a closed shell. For the Te and Xe isotopes, closed shells were observed at $N=82$, $N=112$, and $N=126$. The $S_{2n}$ values of $^{160}$Pd, $^{164}$Cd, $^{182}$Te, and $^{184}$Xe become negative, suggesting that $^{158}$Pd, $^{162}$Cd, $^{180}$Te, and $^{182}$Xe are two neutron drip-line nuclei of the Pd, Cd, Te, and Xe isotopes, respectively. The exploration of neutron drip-lines and the determination of nuclear existence limits are significant in nuclear physics. However, various theoretical studies have demonstrated that neutron drip-line prediction is highly dependent on the model used [87]. For example, $^{160}$Cd, $^{178}$ Te, and $^{180}$Xe are predicted to be two neutron drip-line nuclei using the RMF+CMR method.

Furthermore, $S_{2n}$ was approximately $3-4$ MeV for extremely neutron-rich Pd and Cd isotopes (except for $^{160}$Pd and $^{164}$Cd). This indicates that these nuclei are deeply bound and more likely to be a thick neutron skin than a neutron halo. For extremely neutron-rich Te and Xe isotopes (except for $^{182}$Te and $^{184}$Xe), $S_{2n}$ is approximately $2$ MeV, which tends to support a neutron halo. Owing to the existence of neutron halos, these weakly bound nuclei are very interesting, although they are difficult to obtain experimentally.

The neutron and proton radii distributions are fundamental to nuclear physics and are essential observables that reflect the properties of the nuclei. The charge rms radii for even-even Pd, Cd, Te, and Xe isotopes are shown in Fig. 5. For comparison, the RMF+CMR [44], RMF+BCS [85], and RHB [41] calculations, as well as available experimental data [88], are also shown. Compared with the RMF+CMR and RMF+BCS calculations, the RMF+CMR+BCS results are in good agreement with the RHB calculations. Although the values obtained using the four theoretical methods were slightly lower than those of the available experimental data, they were consistent with the experimental trend with mass number A. This suggests that the RMF+CMR+BCS method is relatively reliable for nuclear property calculations. Moreover, reliable proton rms radii can also be obtained based on the charge rms radii.

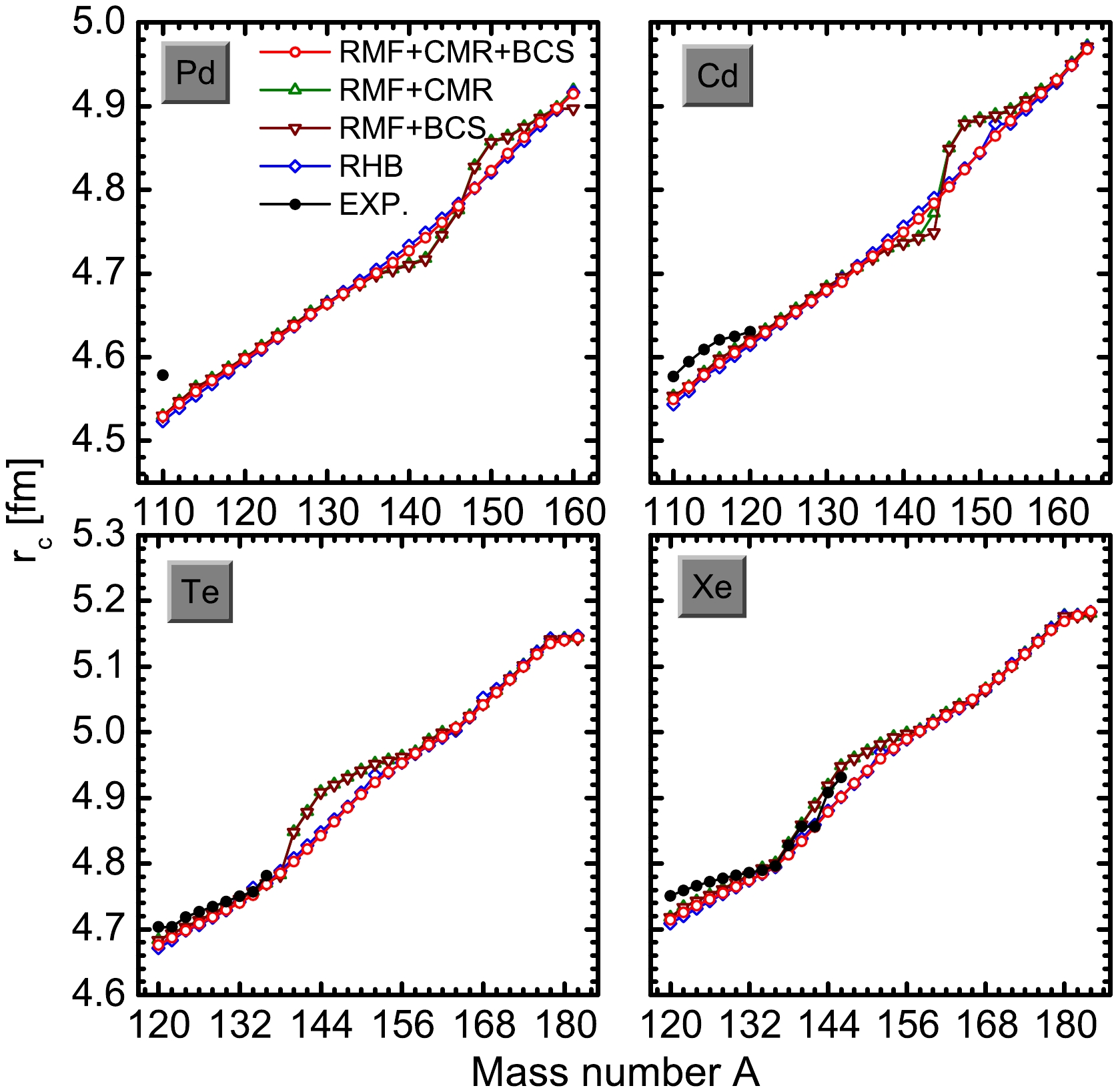
Figure 5.  (color online) Calculated charge rms radii distribution r$_{c}$ of even-even Pd, Cd, Te, and Xe isotopes. The red open circles, green open triangles, purple open inverted triangles, and blue open diamonds correspond to the RMF+CMR+BCS, RMF+CMR, RMF+BCS, and RHB calculations, respectively. The black solid circles represent the available experimental data.

In Fig 6, the neutron and proton rms radii for the even-even Pd, Cd, Te, and Xe isotopes are shown. The results were compared with those of the RMF+CMR [44], RMF+BCS [85], RHB [41] calculations, as well as with $r =r_{0}N^{1/3}$ [9] (black line), where the coefficient $r_{0}$ can be determined by the radii of deeply bound nuclei. The radii trend with mass number A was similar in the four calculations. For the proton rms radii, the results from the four calculations are almost the same. For the neutron rms radii, the results of RMF+CMR+BCS were slightly larger than those of the other three methods. Meanwhile, the neutron rms radii increased sharply and deviated from the $r_{0}N^{1/3}$ trend with mass number A. For the Pd and Cd isotopes, abnormally increasing neutron rms radii were not found, which means that there was no halo or giant halo structure. Nevertheless, the neutron rms radii are remarkably larger than those of the proton for the neutron-rich Pd and Cd isotopes, especially on the extremely neutron-rich side. A fairly thick neutron skin exists, which is critical for studying astrophysical evolution. For the Te and Xe isotopes, the neutron rms radii increased sharply at $A>162$. This is considered strong evidence for the existence of halos, indicating that a neutron halo may exist in these mass regions. The change in radius can be explained by the occupation of the single-particle levels.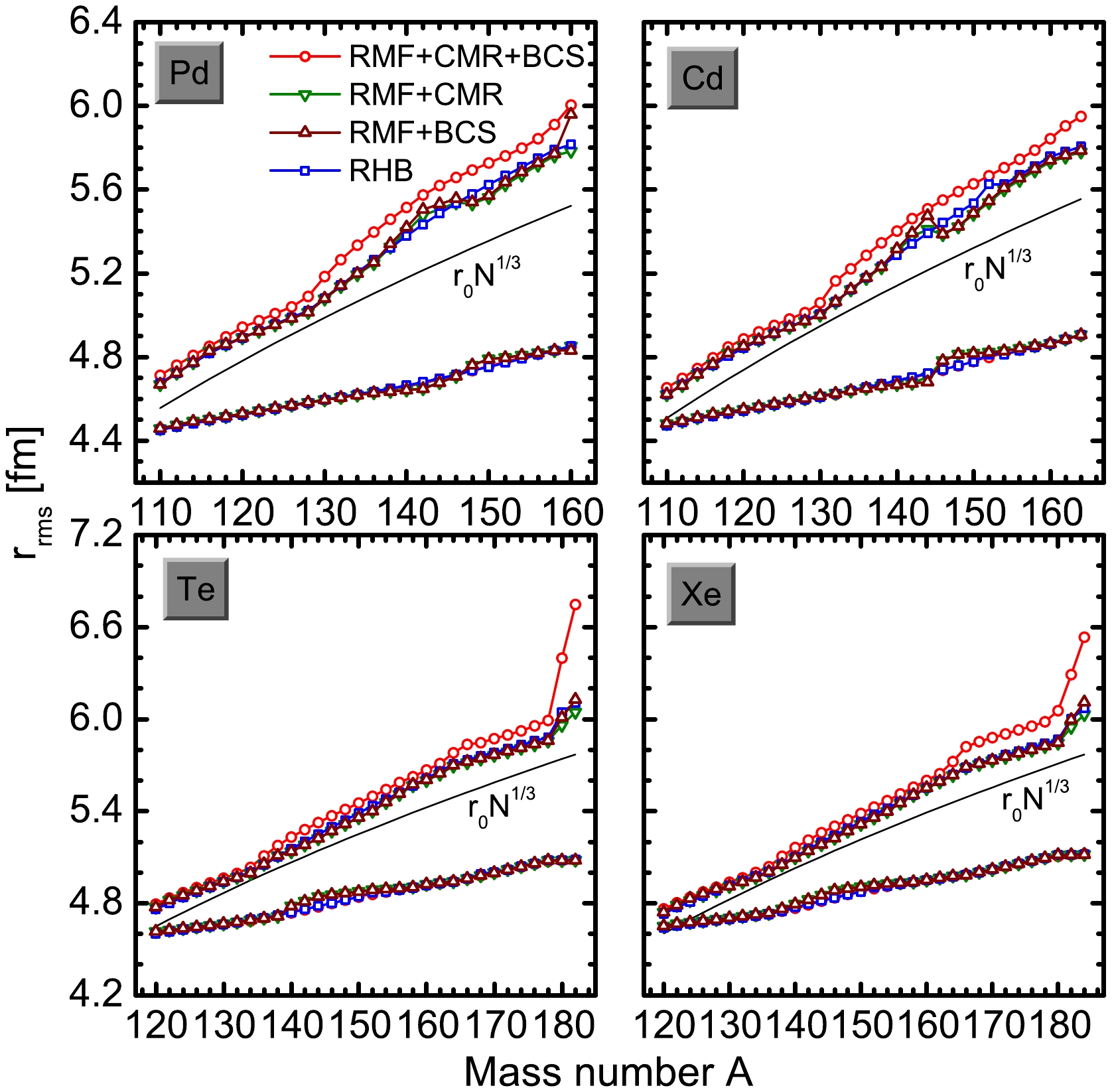

Figure 6.  (color online) Neutron and proton rms radii as a function of mass number A. The red open circles, green open inverted triangles, purple open triangles, and blue open square correspond to the results of the RMF+CMR+BCS, RMF+CMR, RMF+BCS, and RHB methods, respectively. The black solid line corresponds to the radii calculated using the $r_{0}N^{1/3}$ formula, where $r_{0}$ = 1.139 [9].

To reveal the contributions of weakly bound and broad resonant states to the halos, the occupation probabilities of single-particle levels for the even-even Pd, Cd, Te, and Xe isotopes were explored, as shown in Fig. 7. For Pd isotopes, the occupations of levels 2d$_{5/2}$ and 1g$_{7/2}$ were greater than $0.8$ for $A=110$. From $A=110$ to $A=128$, the levels 2d$_{3/2}$, 3s$_{1/2}$, and 1h$_{11/2}$ are gradually occupied until saturated, which supports the traditional magic number $N=82$. From $A=130$ to $A=158$, the occupation probabilities of levels 2f$_{7/2}$, 3p$_{3/2}$, 3p$_{1/2}$, 1h$_{9/2}$, and 2f$_{5/2}$ increase rapidly to saturation, verifying the new magic number $N=112$. Because of the large gap at $N=112$, these neutron-rich nuclei with neutron numbers less than $112$ are relatively bound. The levels 1i$_{13/2}$, 2g$_{9/2}$, 2g$_{7/2}$, and 1i$_{11/2}$ begin to be occupied at $A>158$. When $A=160$, the occupation probabilities of these levels are $0.14$, $0.04$, $0.03$, and $0.008$, respectively. Although the occupation probabilities of these levels are small, their large orbital angular momentum contributes to the level density near the Fermi surface, indicating the formation of a thick neutron skin in extremely neutron-rich Pd isotopes. Similar phenomena were also observed for Cd isotopes. The occupations of levels 1h$_{11/2}$ and 2f$_{5/2}$, as well as those below the orbitals, can reach saturation at $A=130$ ($N=82$) and $A=160$ ($N=112$), respectively. Likewise, there are no weakly bound levels with lower orbital angular momentum occupied by a large numbers of valence neutrons to support the formation of a neutron halo, which means that a thick neutron skin forms in extremely neutron-rich Cd isotopes. For the Te and Xe isotopes, we observe large gaps between levels 1h$_{11/2}$ and 2f$_{7/2}$ as well as 3p$_{1/2}$ and 1i$_{13/2}$, which indirectly suggest the existence of magic numbers $N=82$ and $N=112$. Unlike the Pd and Cd isotopes, the occupation of the weakly bound level 1i$_{13/2}$ almost reaches saturation in$^{178}$Te and $^{180}$Xe. This suggests that the traditional magic number $N=126$ does not disappear. When $N>112$, the resonant levels also begin to be occupied, mainly because the stability of these nuclei becomes very sensitive to pairing effects after considering the pairing correlations. In particular, the occupation of level 3d$_{5/2}$ leads to considerably diffused density distributions, which are responsible for the remarkable increase in neutron rms radii. This further suggests that halos exist in extremely neutron-rich Te and Xe isotopes.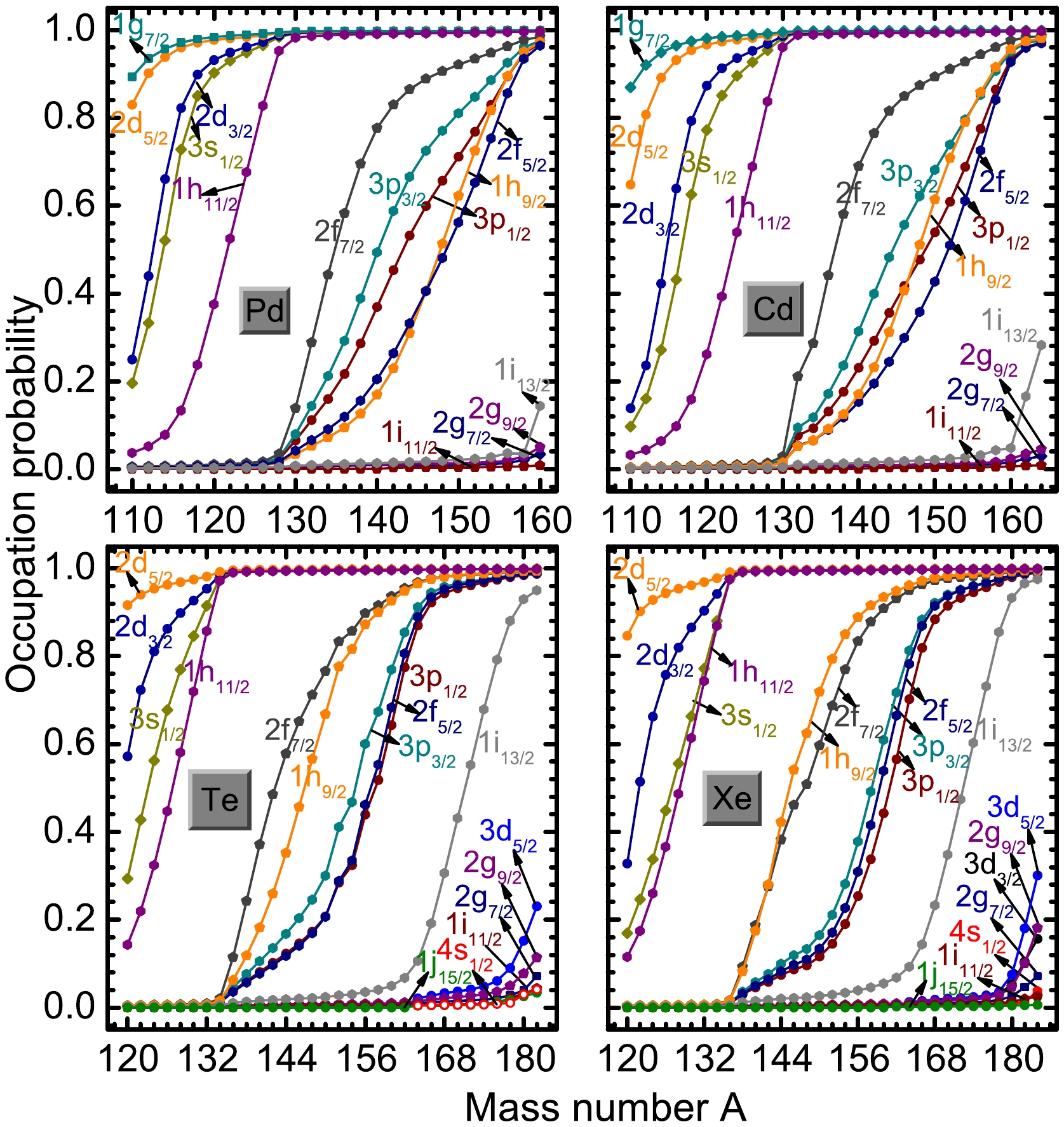

Figure 7.  (color online) Occupation probabilities of neutron single-particle orbitals as a function of mass number A for the even-even Pd, Cd, Te, and Xe isotopes. The labels of the single-particle levels are identical to those in Fig. 1.

To clarify the relationship between single-particle level occupations and radius, the contributions $\Re$ of the single-particle levels to the neutron rms radii are shown in Fig. 8. Namely, $\Re=v_{i}^{2}*<r^{2}_{i}>^{1/2}$, where $v_{i}^{2}$represents the occupation probabilities of the single particle level, and $<r^{2}_{i}>^{1/2}$ represents the rms radii of every single-particle level.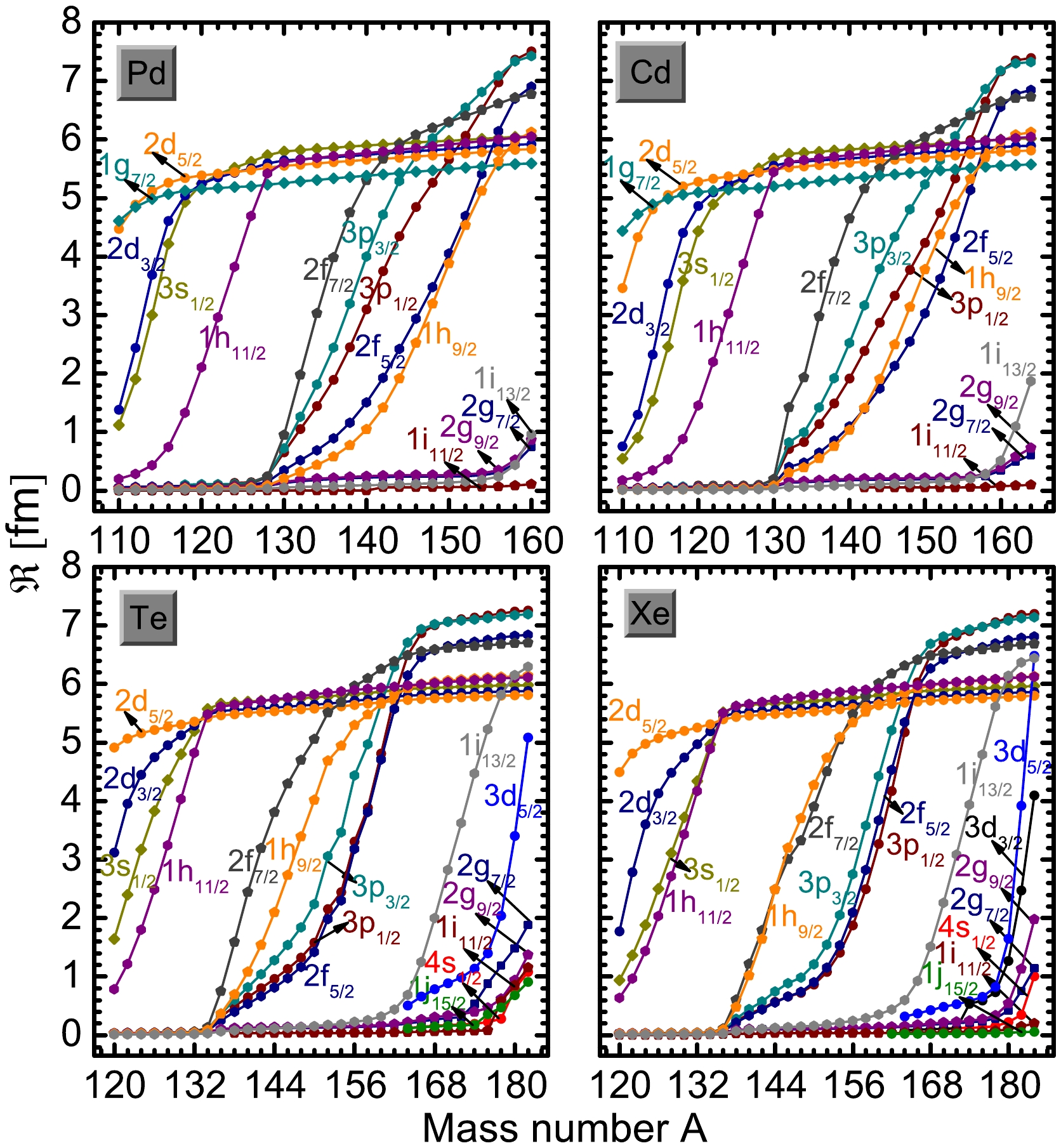

Figure 8.  (color online) Contributions of neutron single-particle levels to the rms as a function of mass number A for Pd, Cd, Te, and Xe isotopes. The labels of the single-particle levels are identical to those shown in Fig. 1.

For the Pd and Cd isotopes, the $\Re$ trend with neutron number N was similar to that of the occupation probabilities. The large gaps between levels 1h$_{11/2}$ and 2f$_{7/2}$ and levels 1h$_{9/2}$ (2f$_{5/2}$) and 1i$_{13/2}$ indirectly indicate the existence of magic numbers $N=82$ and $N=112$.

The $\Re$ values of levels 2d$_{5/2}$ and 1g$_{7/2}$ first rapidly increased and then remained nearly unchanged over the considered range of mass numbers. As the number of neutrons increases, the contributions of levels 2d$_{3/2}$, 3s$_{1/2}$, and 1h$_{11/2}$ to the radii increase rapidly. For the neutron-rich Pd and Cd isotopes, the $\Re$ values of levels 2f$_{7/2}$, 3p$_{3/2}$, 3p$_{1/2}$, 2f$_{5/2}$, and 1h$_{9/2}$ increase rapidly, especially for levels $3$p (3p$_{3/2}$ and 3p$_{1/2}$) and $2$f (2f$_{7/2}$ and 2f$_{5/2}$). However, this was insufficient to cause a significant increase in the neutron rms radii. When $N\geq126$, the $\Re$ values of levels 1i$_{13/2}$, 2g$_{9/2}$, and 2g$_{7/2}$ also began to increase. Their maximum value was only $1.87$. In other words, neutron-rich Pd and Cd isotopes prefer a thick neutron skin rather than a neutron halo. Similar phenomena were observed for the Te and Xe isotopes. A remarkable difference is the contribution of levels 3d$_{5/2}$ (for the Te and Xe isotopes) and 3d$_{3/2}$ (for the Xe isotopes) to the neutron rms radii, where the $\Re$ value increases rapidly on the extremely neutron-rich side. In particular, the $\Re$ value of level 3d$_{5/2}$ rapidly increases after $N=112$, indicating that the unusually large neutron rms radius is mainly due to the contribution of resonant level 3d$_{5/2}$.

The density distributions of the halo nuclei exhibited a long tail at large distances. To further demonstrate the existence of halos, we plot the total proton, neutron, and matter density distributions for even-even Pd, Cd, Te, and Xe isotopes in Fig. 9. The total proton density declines rapidly to zero as r increases, suggesting that the long tail of the total matter density is mainly due to neutron density. For the Pd and Cd isotopes, the neutron density distribution gradually decreased to zero at large distances, resulting in a preference of the neutron skin for a neutron halo. For the Te isotope, although $^{156}$Te and $^{162}$Te are neutron-rich nuclei, their neutron density distributions do not exhibit a long tail. In contrast, the neutron density distributions of $^{168}$Te, $^{174}$Te, and $^{180}$Te become increasingly diffuse with increasing r, showing a long tail that provides direct and obvious evidence for a halo. For Xe isotopes, the neutron density distributions of $^{164}$Xe, $^{170}$Xe, $^{176}$Xe, and $^{182}$Xe drag a long tail with increasing r. These extremely diffuse density distributions are mainly caused by the low-l states, namely, resonant level 3d$_{5/2}$. This suggests that $^{168-180}$Te and $^{164-182}$Xe are neutron halo nuciei, which we expect to be verified experimentally.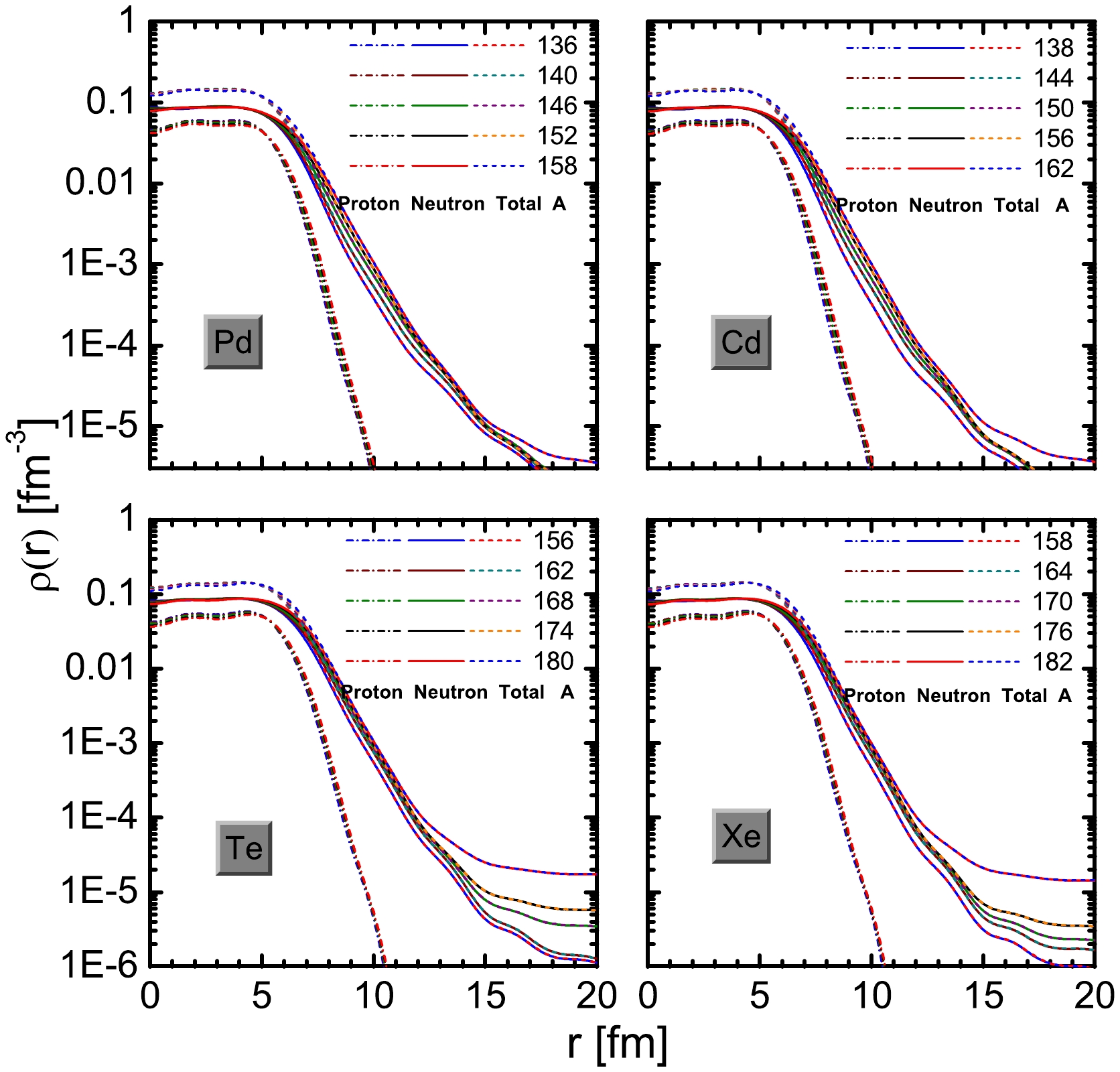

Figure 9.  (color online) Total proton, neutron, and matter density distributions for the even-even Pd, Cd, Te, and Xe isotopes.

To further explain the halo phenomena, we investigated the contributions of different single-particle levels to the neutron density distribution. The density ratio, which is the ratio of the single-particle level density to the total neutron density $\rho_{lj}(r)/\rho(r)$, for $^{150}$Pd, $^{160}$Cd, $^{178}$Te, and $^{180}$Xe is shown in Fig. 10. The density ratios of bound levels 2f$_{7/2}$, 2f$_{5/2}$, 3p$_{3/2}$, and 3p$_{1/2}$ were very large at $r=9-13$ fm, which significantly contributed to the increase in neutron radii. With a further increase in r, the density ratios of all bound states declined to zero. In contrast, the density ratios of resonant levels are diffuse. Although the level 1i$_{13/2}$ is a resonant state, it has an extremely high orbital angular momentum. Therefore, the contribution of level 1i$_{13/2}$ to the diffuse density distribution was relatively small.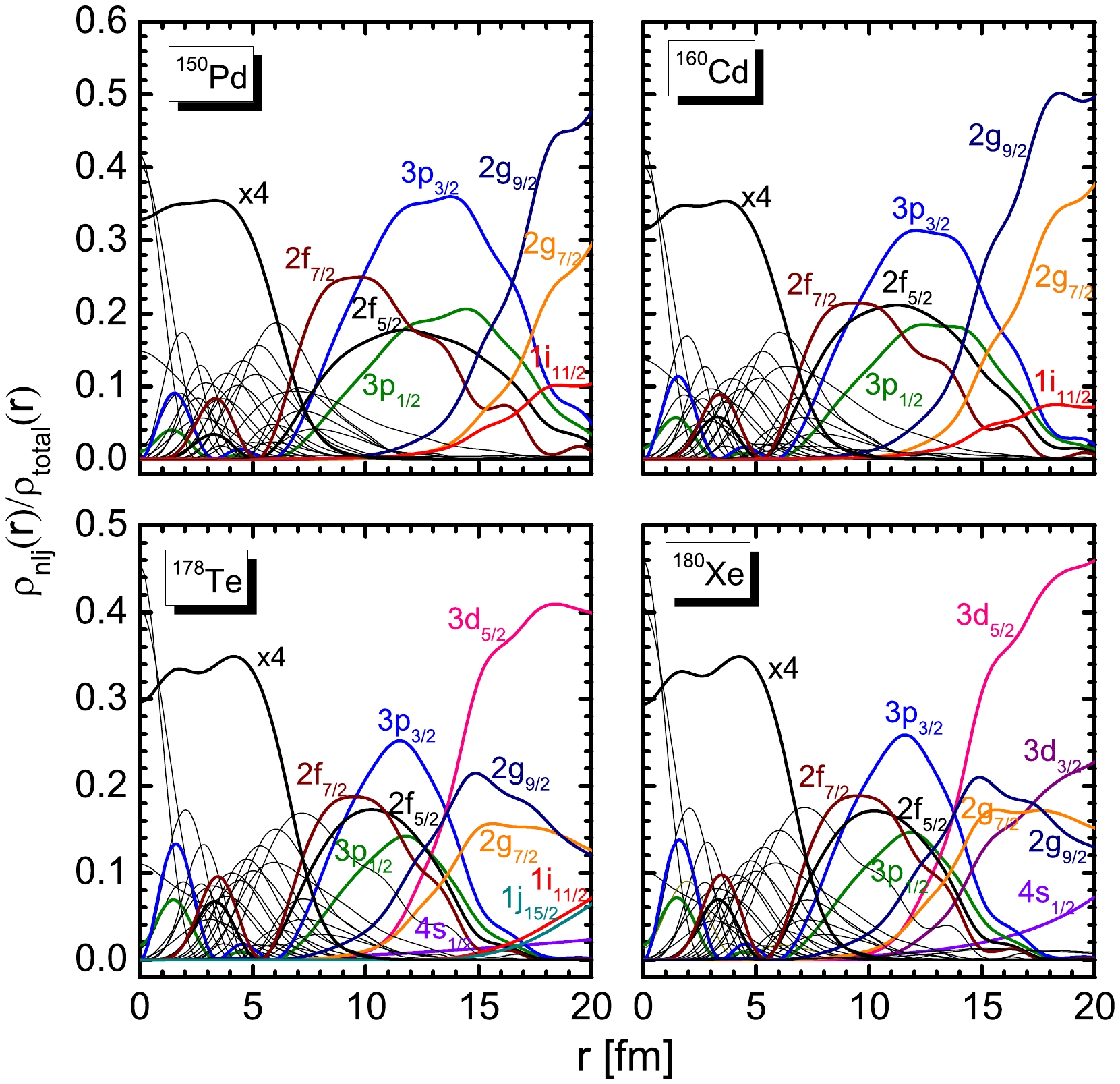

Figure 10.  (color online) Relative contributions of different levels to the total neutron density in $^{150}$Pd, $^{160}$Cd, $^{178}$Te, and $^{180}$Xe. The orbitals located near the particle continuum threshold are marked with different colors.

For $^{150}$Pd and $^{160}$Cd, the density ratios of the resonant levels 2g$_{9/2}$, 2g$_{7/2}$, and 1i$_{11/2}$ were considerably large in the range from $r=15$ fm to $r=20$ fm, indicating that the neutron density distribution mainly originated from the contribution of resonant states. However, the contrbutions of these levels to absolute density distributions were relatively small because of the large centrifugal barrier, which confined them more tightly around the nucleus, and their low occupancy. This results in $^{150}$Pd and $^{160}$Cd preferring a neutron skin to a neutron halo. For $^{178}$Te, the contributions of the resonant levels 2g$_{9/2}$, 2g$_{7/2}$, 1i$_{11/2}$, and 1j$_{15/2}$ to the diffuse density distributions were also relatively weak due to a large centrifugal barrier. The long tail of the neutron density distributions comes mainly from the contribution of resonant level 3d$_{5/2}$, which plays a critical role in the halo structure in $^{178}$Te. Similar phenomena were observed for $^{180}$Xe. Unlike $^{178}$Te, the halo structure in $^{180}$Xe comes mainly from the contributions of resonant levels 3d$_{5/2}$ and 3d$_{3/2}$. It can be concluded that the single-particle levels around the Fermi surface, particularly the resonant levels with low orbital angular momentum, contribute to the diffuse density distribution.

To explore the contribution of the broad resonant states to the diffuse density distribution, the wavefunctions of single-particle levels for $^{150}$Pd, $^{160}$Cd, $^{178}$Te, and $^{180}$Xe are plotted. The real and imaginary parts of the upper and lower components are shown in Fig. 11. Compared to the upper component $f(r)$, the contribution of the lower component g(r) to the density distributions is insignificant. For $^{150}$Pd, the upper component $f(r)$ of bound level 3p$_{1/2}$ gradually decreases to zero with increasing r. For resonant states 2g$_{9/2}$, 2g$_{7/2}$, and 1i$_{11/2}$, regardless of the real or imaginary part, the upper component $f(r)$ of their wavefunctions extends over a large range. Similar phenomena were observed for $^{160}$Cd. Although resonant levels 2g$_{9/2}$, 2g$_{7/2}$, and 1i$_{11/2}$ have a large centrifugal barrier and weakly contribute to the diffuse density distribution, they can lead to relatively high level densities near the Fermi surface. For $^{178}$Te, the real and imaginary parts of the upper components $f(r)$ of resonant levels 3d$_{5/2}$, 2g$_{7/2}$, 1i$_{11/2}$, and 4s$_{1/2}$ extend over a large range with increasing r. Similar to those of resonant states 2g$_{7/2}$ and 1i$_{11/2}$ in $^{150}$Pd and $^{160}$Cd, the contributions of these two resonant levels to the diffuse density distribution are relatively insignificant. For $^{180}$Xe, the upper component $f(r)$ of resonant levels 3d$_{5/2}$, 2g$_{7/2}$, 4s$_{1/2}$, and 3d$_{3/2}$extends over a large distance in both the real and imaginary parts. Similarly, the contribution of level 2g$_{7/2}$ to the diffuse density distribution is weak owing to the large centrifugal barrier. These results indicate that narrow resonant and bound states barely contribute to the diffuse density distribution. The diffuse density distribution mainly originates from resonance levels with lower orbital angular momentum, such as the broad resonant state 3d$_{5/2}$. The resonant states 3d$_{3/2}$ and 4s$_{1/2}$ also have a certain impact on the diffuse density distribution.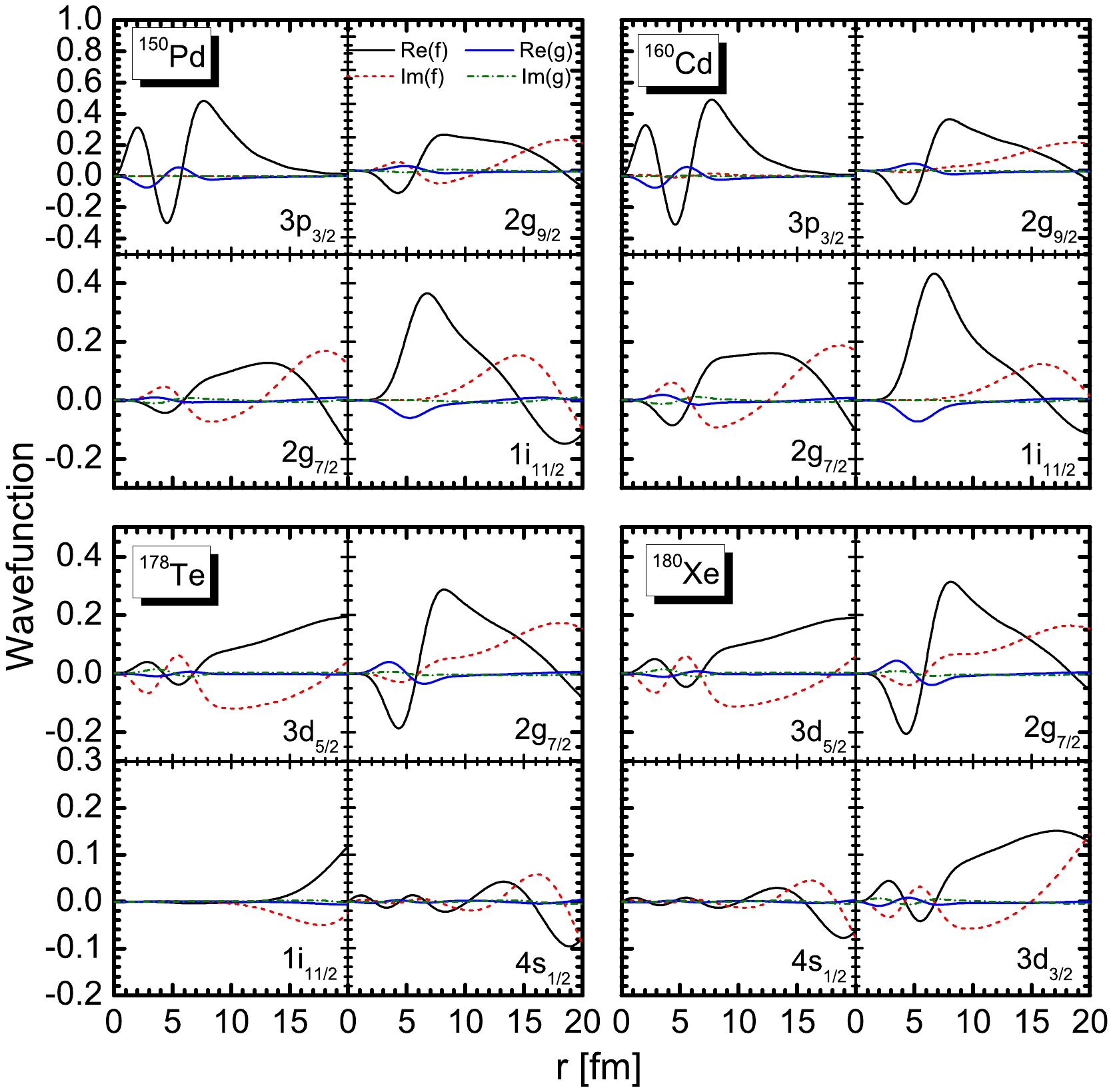

Figure 11.  (color online) Wavefunctions of the single-particle levels near the continuum threshold for $^{150}$Pd, $^{160}$Cd, $^{178}$Te, and $^{180}$Xe. The black solid and red dashed lines represent the real and imaginary parts of the upper component f(r), respectively. The blue solid and green dash-dotted lines represent the real and imaginary parts of the lower component g(r), respectively.

The exotic properties of neutron-rich Pd, Cd, Te, and Xe isotopes were systematically studied using the newly developed RMF+CMR+BCS method with the functional NL3*. The nucleon pairing correlations and couplings with the continuum were treated appropriately. The results were compared with those of RMF+CMR, RMF+BCS, and RHB calculations as well as available experimental data. The two-neutron separation energies $S_{2n}$ and charge rms radii were well reproduced.

The calculated single-particle levels supported the traditional magic number $N=82$ and verified the existence of a new magic number $N=112$ in Pd and Cd isotopes, while the magic number $N=126$ disappeared in extremely neutron-rich Pd and Cd isotopes. For the Te and Xe isotope, we did not observe the disappearance of the traditional magic numbers. Although magic numbers $N=112$ and $N=126$ exist in the neutron-rich Te and Xe isotopes, the shell gap is weakened, and the valence neutrons are easily scattered into broad resonant levels 3d$_{5/2}$ and 3d$_{3/2}$ due to the pairing correlations, causing halo formation. To explore the effect of pairing correlations and resonances on the exotic phenomena, two different types of neutron numbers were defined, namely, the number of neutrons occupying above the Fermi surface, $N_{\lambda}$, and the number of neutrons occupying above zero potential energy surface, $N_{0}$. The evolution of $N_{\lambda}$ and $N_{0}$ with the mass number A is consistent with the trend of single-particle levels, suggesting that pairing correlations play a crucial role in the halo and change in magic numbers.

The two neutron separation energies $S_{2n}$ of the Pd, Cd, Te, and Xe isotopes were also calculated. The calculation results are in agreement with the available experimental data. The evolution trend of $S_{2n}$ with the mass number A clearly shows the neutron magic numbers $N=82$, $112$ for the Pd and Cd isotopes and $N=82$, $112$, $126$ for the Te and Xe isotopes. $^{158}$Pd, $^{162}$Cd, $^{180}$Te, and $^{182}$Xe are the two neutron drip-line nuclei of the Pd, Cd, Te, and Xe isotopes, respectively.

Subsequently, to investigate the possible exotic structures in neutron-rich Pd, Cd, Te, and Xe isotopes, the rms radii, occupation probabilities of single-particle levels, contributions of single-particle levels to the neutron rms radii, and total proton, neutron, and matter density distributions were investigated. The neutron rms radii increased sharply in the neutron-rich Te and Xe isotopes, especially in weakly bound nuclei close to the neutron drip-line. This is an evident deviation from the traditional rule $r\propto N^{1/3}$. Meanwhile, the contributions of broad resonant states 3d$_{5/2}$ and 3d$_{3/2}$ became significant in these nuclei. Furthermore, very diffuse density distributions were observed in $^{168,174,180}$Te and $^{164,170,176,182}$Xe, implying that they are neutron halos. Different from the neutron-rich Te and Xe isotopes, the neutron density distributions of the neutron-rich Pd and Cd isotopes decreased gradually to zero and tended to support a neutron skin rather than neutron halo.

Finally, the occupations of bound levels with lower orbital angular momentum were determined to be the main reason for the increase in radii by analyzing the contributions of different single-particle levels to the total density and wavefunction. In comparison, diffuse density distributions, such as halos, originate mainly from the contributions of resonant levels with lower orbital angular momentum near the continuum threshold. The prediction of exotic structures such as halos and skins in neutron-rich Pd, Cd, Te, and Xe isotopes is valuable for experimental investigations.

The authors are grateful to Jian-You Guo for providing constructive guidance and valuable suggestions.