-
In the recent
$ \mathrm{LHCb} $ experiment at$ \mathrm{CERN} $ , researchers reported an exciting discovery of a particle known as$ \Xi_{cc}^{++} $ [1, 2]. This groundbreaking finding has sparked significant interest in the exploration of double charm baryons. Specifically, the$ \Xi_{cc}^{++} $ particle is formed by the combination of two heavy quarks with a single light quark, resulting in a highly distinctive structure. In this study, we adopt an assumption of potential models, which suggests that the interaction between heavy quarks and anti-quarks within hadrons can be described by a potential energy [3].Although lattice gauge theory remains a fundamental tool for studying non-perturbative phenomena in Quantum Chromodynamics
$ \mathrm{(QCD)} $ , its investigation of the doubly heavy baryon potential has been relatively limited to date [4, 5]. In contrast, gauge/gravity duality provides a new theoretical tool for studying strongly coupled gauge theories. Furthermore, in Ref. [6], the holographic potential of quark-antiquark pairs was computed for the first time. Based on the study in Ref. [6], the potential was further investigated in Refs. [7, 8] to examine the potential at finite temperature. In recent years, the methodology of utilizing holographic theories to study multi-quark potentials has been increasingly refined. The obtained multi-quark potentials from holography are in good agreement with lattice calculations and$ \mathrm{QCD} $ phenomenology [9−20]. The techniques employed to extract the$ {QQq} $ potential in our study are analogous to those used in lattice$ \mathrm{QCD} $ [21].The creation of quark-gluon plasma
$ \mathrm{(QGP)} $ via high-energy heavy-ion collisions allows us to simulate the high temperature and density conditions of the early universe [22−25]. The formation of this$ \mathrm{QGP} $ is crucial for our understanding of the early stages of cosmic evolution and the fundamental properties of quark color dynamics. At low temperatures, quarks and gluons are confined within hadrons. As the separation between quarks increases, the strong interaction force becomes stronger. When the separation reaches a limit, new quark-antiquark pairs are typically produced, resulting in the confinement of quarks within hadrons. This behavior is manifested as string breaking in this study. Under extreme conditions, the strong interaction between hadrons diminishes at long range, allowing quarks to move freely over larger distances [26−28].In heavy-ion collision experiments, heavy ions collide at speeds close to the speed of light, forming
$ \mathrm{QGP} $ [25]. Similar to the early universe, this substance does not remain stationary but rapidly expands. Therefore, when studying the doubly heavy baryon, the effect of rapidity should be considered. This is crucial for understanding the interaction between$ {QQq} $ and the medium, as well as the transport properties within the$ \mathrm{QGP} $ . By examining the behavior of moving$ {QQq} $ , more comprehensive information about the$ \mathrm{QGP} $ can be obtained, leading to further investigation into the properties of$ \mathrm{QCD} $ . Furthermore, by studying the variation in string breaking under different temperature and rapidity conditions, we can investigate decay rates of different hadrons under varying conditions [29].Gauge/gravity duality was initially proposed by Maldacena [30] for conformal field theories, and it was later extended to include theories resembling
$ \mathrm{QCD} $ , establishing a connection between string theory and heavy-ion collisions in some manner [31−33]. The study of moving heavy quarkonium can be found in Refs. [34−50].The remaining sections of this paper are as follows. In Sec. II, we construct string configurations considering the effects of finite temperature and finite rapidity. In Sec. III, we discuss the computation of the model's potential energy. At first, we calculate the influence of rapidity on the string breaking of
${QQq} $ . Then, we discuss its screening and provide a comprehensive comparison with$ {Q\bar{Q}} $ . Additionally, we plot their state diagrams in the$ T- \eta $ plane. Finally, we summarize these findings in Sec. IV. -
First, the background metric at a finite temperature can be expressed as [13, 14, 51−53]:
$ {\rm d} s^{2}=w(r) \Big (-f(r){\rm d}t^{2}+ {\rm d}\vec{x}^{2} +\frac{1}{f(r)}{\rm d}r^{2} \Big )+ {\rm e}^{-\mathbf{s}r^{2}}g_{ab}^{(5)}{\rm d}\omega^{a}{\rm d}\omega^{b}, $

(1) where
$ \begin{aligned}[b] w(r)&=\frac{{\rm e}^{\mathbf{s}r^{2}}R^{2}}{r^{2}}\,,\\ f(r)&=1-\frac{r^{4}}{r_{h}^{4}}. \end{aligned} $

(2) The metric represents a one-parameter deformation of Euclidean
$ \mathrm{AdS_5}\times\mathrm{S_5} $ space, parametrized by$ \mathbf{s} $ and with a radius R. It comprises a five-dimensional compact space (sphere)$ \mathrm {X} $ with coordinates$ \omega^{a} $ , a blackening factor$ f(r) $ , and a black hole horizon (brane) at$ r_h $ . The Hawking temperature of the black hole T is defined as follows:$ T=\frac{1}{4\pi}{\left | \frac{{\rm d}f}{{\rm d}r} \right |}_{r=r_{h}}=\frac{1}{\pi r_{h}}. $

(3) In this study, we investigate the motion of a particle comprising two heavy quarks and one light quark in a thermal medium. We divide the particle's spatial coordinates into three directions:
$ x_{1} $ (connecting the heavy quark pair),$ x_{2} $ , and$ x_{3} $ (perpendicular to the heavy quark pair). We determine that the coefficients of$ x_1 $ and$ x_2 $ in the metric are the same, which implies that the presence of the heavy quark pair at either$ x_1 $ or$ x_2 $ does not affect the calculation results. Given that temperature and rapidity are constant, we can consider the doubly heavy baryon to be in a state of force equilibrium. Furthermore, energy loss is not considered in this study. Hence, it can be discussed in future studies.In our study, we consider that
${QQq} $ is moving with a constant rapidity η along$ x_{3} $ direction [34−36, 43, 46]. For convenience, let us consider a new scenario in which${QQq} $ is at rest, while the surrounding medium is in motion relative to it. We then introduce the Lorentz transform to reflect the effect of rapidity η on it and obtain the new metric:$ \begin{aligned}[b] {\rm d}s^{2}=\;&w(r)\Big(-g_{1}(r){\rm d}t^{2} -2\sinh(\eta)\cosh(\eta)\Big(1-\frac{g_{1}(r)}{g_{2}(r)}\Big){\rm d}x_{3}{\rm d}t\\ &+g_{3}(r){\rm d}x_{3}^{2}+{\rm d}x_{1}^{2}+{\rm d}x_{2}^{2}+\frac{g_{2}(r)}{g_{1}(r)}{\rm d}r^{2}\Big)+{\rm e}^{-\mathbf{s}r^{2}}g_{ab}^{(5)}{\rm d}\omega^{a}{\rm d}\omega^{b}, \end{aligned} $

(4) where
$ \begin{aligned}[b] g_{1}(r)&=f(r)\cosh^{2}(\eta)-\sinh^{2}(\eta),\\g_{2}(r)&=\frac{g_{1}(r)}{f(r)},\\g_{3}(r)&=\cosh^{2}(\eta)-f(r)\sinh^{2}(\eta). \end{aligned} $

(5) The Nambu-Goto action of a string can be expressed as follows:
$ S_{NG} = - \frac{1}{2\pi\alpha'} \int {\rm d}\xi^{0} {\rm d}\xi^{1} \sqrt{- \det g_{ab}}, $

(6) where
$ \alpha' $ denotes a constant, ($ \xi^{0} $ ,$ \xi^{1} $ ) denote worldsheet coordinates, and$ g_{ab} $ denotes an induced metric. We introduce the baryon vertex and heavy and light quarks to construct the${QQq} $ configuration. Then, we know from$ \mathrm{AdS/CFT} $ that the vertex is a five brane [54, 55]. At leading order in$ \alpha' $ , the baryon vertex action is$S_{\rm vert}= \mathrm{\tau}_{5}\int {\rm d}^{6}\xi \sqrt{\gamma^{(6)}}$ , where$ \tau_{5} $ denotes the brane tension and$ \xi^{i} $ denotes the worldvolume coordinates. Given that the brane is wrapped on$ \mathrm {X} $ interior space, it looks point-like in$ \mathrm{AdS_5} $ . We select a static gauge$ \xi^{0}=t,\,\xi^{a}=\theta^{a} $ with$ \theta^{a} $ as the coordinates on$ \mathrm {X} $ . Hence, the following holds.$ S_{\rm vert}=\tau_{v}\int {\rm d}t\frac{{\rm e}^{-2\mathbf{s}r^2}}{r} \sqrt{g_{1}(r)}, $

(7) where
$ \tau_{v} $ denotes a dimensionless parameter defined by$ \tau_{v}=\mathrm{\tau}_{5}R\mathrm{vol(X)} $ and$ \mathrm{vol(X)} $ denotes a volume of$ \mathrm {X} $ .Finally, we consider the light quark at the end of the string as a tachyon field, which couples to the worldsheet boundary by
$S_q=\int {\rm d}\tau \mathbf{e} {T}$ [56, 57]. This term is typical for strings propagating in an open string tachyon background and${T}$ is its background scalar [56]. The integral over a worldsheet boundary, parameterized by τ and$ \mathbf{e} $ , represents the boundary metric. In this study, we can assume${T}$ to be a constant${T}_{0}$ , and the integral reduces to a coordinate integral of t. Thus, the the following holds.$ S_{q}=m\int {\rm d}t\frac{{\rm e}^{\frac{\mathbf{s}r^2}{2}}}{r} \sqrt{g_{1}(r)}, $

(8) where
$m=R {T}_{0}$ . This shows that a particle with mass${T}_{0}$ is at rest, while the surrounding medium with temperature T moves relative to it with rapidity η. The selected parameters are as follows:$g=\dfrac{R^2}{2\pi\alpha'}= 0.176,\,\; k=\dfrac{\tau_{v}}{3g}=$ $-0.321, n=\dfrac{m}{g}=3.057,\;\mathbf{s}=0.45\,\mathrm{GeV^2},\,\,c=0.623\,\mathrm{GeV}$ [20]. -
As shown in Fig. 1, the heavy quark pair, light quark, and baryon vertex are connected by three strings. Specifically, the separation distance between the heavy quark pair is denoted as L. Therefore, we can express the total action as follows:

Figure 1. (color online) String configuration at a small separation distance of heavy quark pair. We use the line connecting two heavy quarks
${Q}$ as the$ x_1 $ -axis, while the baryon vertex$ {v} $ and light quark$ {q} $ are on the r-axis. The rapidity η is along the$ x_3 $ -axis direction. The heavy quark, light quark, and baryon vertex are connected by blue strings. The black arrows represent generalized forces. Furthermore,$ r_{h} $ denotes the position of the black hole horizon.$ r_{w} $ denotes the position of an imaginary wall when$ {QQq} $ is confined.$ S=\sum\limits_{i=1}^{3} S_{\rm NG}^{(i)}+S_{\rm vert}+S_{q}. $

(9) According to a previous discussion, given that the results obtained from
$ x_{1} $ and$ x_{2} $ are the same, we directly designate the line where the heavy quark pair is located as$ x_1 $ . Furthermore, the rapidity perpendicular to the$ x_1 $ direction corresponds to$ x_3 $ , as shown in Fig. 1. Hereafter, we refer to$ x_1 $ as x. Then, in this configuration, we choose the static gauge where$\xi^{0}=t,\,\,\xi^{1}=r$ , and we consider x as a function of r. Therefore, the total sum of the Nambu-Goto action can be expressed as:$ \begin{aligned}[b] \sum\limits_{i=1}^{3} S_{\rm NG}^{(i)}=\;&2g \int_{0}^{t} {\rm d} t \int_{0}^{r_{v}} w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)} {\rm d} r\\&+g\int_{0}^{t} {\rm d} t \int_{r_{v}}^{r_{q}} w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)} {\rm d} r, \end{aligned} $

(10) where
$ \partial_{r}x=\dfrac{\partial x}{\partial r} $ and$ x(r) $ satisfy the following boundary conditions:$ \begin{aligned}[b]& x(0)=\pm\,\frac{L}{2},\,x(r_{v})=x(r_{q})=0,\,\\& \begin{cases} (\partial_{r}x)^2=\cot^2(\alpha),&r=r_{v}\\ (\partial_{r}x)^2=0,&r\in (r_{v},r_{q}]. \end{cases} \end{aligned} $

(11) Now, we combine the baryon vertex and light quark as follows:
$ \begin{aligned}[b] S=\;>\Big(2\int_{0}^{r_{v}} w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)} {\rm d} r\\&+ \int_{r_{v}}^{r_{q}} w(r)\sqrt{g_{2}(r)}{\rm d} r\\ &+3k\frac{{\rm e}^{-2\mathbf{s}r^2}}{r} \sqrt{g_{1}(r)}+n\frac{{\rm e}^{\frac{\mathbf{s}r^2}{2}}}{r} \sqrt{g_{1}(r)}\Big). \end{aligned} $

(12) It is easy to observe that the first term is divergent. Hence, we obtain the potential energy according to
$ E=S/t $ after normalization as follows:$ \begin{aligned}[b] E_{QQq}=\;&g\Big(2\int_{0}^{r_{v}} \big(w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}-\frac{1}{r^{2}}\big){\rm d}r-\frac{2}{r_{v}}\\&+\int_{r_{v}}^{r_{q}} w(r)\sqrt{g_{2}(r)}{\rm d}r\\ &+3k\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}+n\frac{{\rm e}^{\frac{\mathbf{s}r_{q}^2}{2}}}{r_{q}} \sqrt{g_{1}(r_{q})}\Big)+2c. \\[-14pt] \end{aligned} $

(13) where
$ r_{v} $ denotes the independent variable at fixed T and η. By substituting the first term of the unnormalized energy into the Euler-Lagrange equation, we obtain:$ \mathcal{H}=\frac{w(r)g_{1}(r)\partial_{r}x}{\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}}, $

(14) Given that
$ \mathcal{H} $ is a constant, we obtain the following.$ \mathcal{H}|_{r=r_{v}}=\frac{w(r_{v})g_{1}(r_{v})\cot (\alpha)}{\sqrt{g_{1}(r_{v})\cot^2(\alpha)+g_{2}(r_{v})}}. $

(15) According to
$ \mathcal{H}=\mathcal{H}|_{r=r_{v}} $ ,$\begin{aligned}[b]& \partial_{r}x=\\&\sqrt{\frac{w(r_{v})^{2}g_{1}(r_{v})^{2}g_{2}(r)}{w(r)^{2}g_{1}(r)^{2}\big(g_{1}(r_{v})+g_{2}(r_{v})\tan^2(\alpha)\big)-g_{1}(r)w(r_{v})^{2}g_{1}(r_{v})^{2}}}. \end{aligned} $

(16) Now, we determine the position of the light quark
$ r_{q} $ and angle α between the string and x-axis at the baryon vertex. The generalized force equilibrium equations at the baryon vertex and light quark must be equal to zero. First, we consider the variation of their respective action quantities to obtain their generalized forces as follows:$ e_{1}=gw(r_{v})\Big(-\sqrt{\frac{g_{1}(r_{v})f(r_{v})}{f(r_{v})+\tan^{2}\alpha}},\,-\sqrt{\frac{g_{1}(r_{v})}{f(r_{v})^2\cot^2(\alpha)+f(r_{v})}}\Big), $

(17) $ e_{2}=gw(r_{v})\Big(\sqrt{\frac{g_{1}(r_{v})f(r_{v})}{f(r_{v})+\tan^{2}\alpha}},\,-\sqrt{\frac{g_{1}(r_{v})}{f(r_{v})^2\cot^2(\alpha)+f(r_{v})}}\Big), $

(18) $ e_{3}=gw(r_{v})\big(0,\,\sqrt{g_{2}(r_{v})}\big), $

(19) $ e_{3}'=gw(r_{q})\big(0,\,-\sqrt{g_{2}(r_{q})}\big), $

(20) $ f_{q}=\Big(0,\,-gn\partial_{r_{q}}\big(\frac{{\rm e}^{\frac{\mathbf{s}r_{q}^2}{2}}}{r_{q}} \sqrt{g_{1}(r_{q})}\big)\Big), $

(21) $ f_{v}=\Big(0,\,-3gk\partial_{r_{v}}\big(\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}\big)\Big), $

(22) where
$ e_{i} $ denotes the string tension, and$ f_{q} $ and$ f_{v} $ denote the forces provided by the light quark and baryon vertices, respectively [20].It is evident that the generalized force equilibrium equation at the light quark is solely a function of
$ r_{q} $ and can be expressed as follows:$ F_{1}(r_{q})=\frac{f_{q}+e_{3}'}{gw(r_{q})}=0. $

(23) Additionally, we can solve for
$ r_{q} $ based on this equation by changing T and η. The force balance equation at the vertex is as follows:$ \begin{array}{*{20}{l}} f_{v}+e_{3}+e_{1}+e_{2}=0. \end{array} $

(24) In addition to T and η, the equation has only two unknowns,
$ r_{v} $ and α, By solving the equation, we can obtain the function of α as a function of$ r_{v} $ . Then, we can express distance L as a function of$ r_{v} $ :$ L=2\int_{0}^{r_{v}}\frac{\partial x}{\partial r} {\rm d} r. $

(25) Together with Eqs. (13) and (25), we can numerically solve the energy at small L.
-
According to Fig. 2, when compared to small L, intermediate L is only missing a straight string from
$ r_{v} $ to$ r_{q} $ , and the sum of the action can be expressed as
Figure 2. (color online) String configuration at an intermediate separation distance of a heavy quark pair. We use the straight line between two heavy quarks
$ {Q} $ as$ x_1 $ -axis, and baryon vertex and light quarks are in the same position on the r-axis. Rapidity η is along$ x_3 $ -axis direction. The black arrows represent generalized forces. Furthermore,$ r_{h} $ denotes the position of the black hole horizon. Additionally,$ r_{w} $ denotes the position of an imaginary wall when${QQq}$ is confined.$ S=\sum\limits_{i=1}^{2} S_{\rm NG}^{(i)}+S_{\rm vert}+S_{q}. $

(26) We chose the same static gauge as selected earlier. It is easy to show that the sum of Nambu-Goto action becomes:
$ \sum\limits_{i=1}^{2} S_{\rm NG}^{(i)}=2g \int_{0}^{t} {\rm d}t \int_{0}^{r_{v}} w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)} {\rm d}r. $

(27) Then, the boundary condition becomes:
$ x(0)=\pm\,\frac{L}{2},~~x(r_{v})=0,~~(\partial_{r}x|_{r=r_{v}})^2=\cot^2(\alpha). $

(28) Therefore, the potential energy can be expressed as
$ \begin{aligned}[b] E_{QQq}=\;&g\Big(2\int_{0}^{r_{v}} \big(w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}-\frac{1}{r^{2}}\big){\rm d}r-\frac{2}{r_{v}}\\ &+3k\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}+n\frac{{\rm e}^{\frac{\mathbf{s}r_{v}^2}{2}}}{r_{v}} \sqrt{g_{1}(r_{v})}\Big)+2c. \end{aligned} $

(29) Finally, we can write the equation for the equilibrium of generalized force at the coincidence of the light quark and the baryon vertex as
$ \begin{array}{*{20}{l}} f_{v}+f_{q}+e_{1}+e_{2}=0, \end{array} $

(30) and each force can be expressed as
$ e_{1}=gw(r_{v})\Big(-\sqrt{\frac{g_{1}(r_{v})f(r_{v})}{f(r_{v})+\tan^{2}\alpha}},\,-\sqrt{\frac{g_{1}(r_{v})}{f(r_{v})^2\cot^2(\alpha)+f(r_{v})}}\Big), $

(31) $ e_{2}=gw(r_{v})\Big(\sqrt{\frac{g_{1}(r_{v})f(r_{v})}{f(r_{v})+\tan^{2}\alpha}},\,-\sqrt{\frac{g_{1}(r_{v})}{f(r_{v})^2\cot^2(\alpha)+f(r_{v})}}\Big), $

(32) $ f_{q}=\Big(0,\,-gn\partial_{r_{v}}\big(\frac{{\rm e}^{\frac{\mathbf{s}r_{v}^2}{2}}}{r_{v}} \sqrt{g_{1}(r_{v})}\big)\Big), $

(33) $ f_{v}=\Big(0,-3gk\partial_{r_{v}}\big(\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}\big)\Big). $

(34) According to Eqs. (25) and (29), we can obtain the energy at intermediate L:
-
As observed in Fig. 3, the configuration comprises two strings, the vertex, and the light quark. However, due to the presence of smooth turning points on the strings, we can utilize a new static gauge that simplifies the calculations. In this gauge, we set
$ \xi^{0}=t,\,\xi^{1}=x $ , and consider r as a function of x. Accordingly, we can express the total action as follows:
Figure 3. (color online) String configuration at a large separation distance of a heavy quark pair. We use the straight line between two heavy quarks
$ {Q} $ as the$ x_1 $ -axis, and baryon vertex and light quarks are in the same position on the r-axis. The rapidity η is along the$ x_3 $ -axis direction. There is a smooth turning point on each of the two strings. The black arrows represent generalized forces.$ r_{h} $ denotes the position of the black hole horizon.$ r_{w} $ denotes the position of an imaginary wall when the$ \mathrm{QQq} $ is confined.$ \begin{aligned}[b] S=\;>\Big(\int_{-\frac{L}{2}}^{0} w(r)\sqrt{g_{1}(r)+g_{2}(r)(\partial_{x}r)^2} {\rm d} x\\&+\int_{0}^{\frac{L}{2}} w(r)\sqrt{g_{1}(r)+g_{2}(r)(\partial_{x}r)^2}{\rm d} x\\ &+3k\frac{{\rm e}^{-2\mathbf{s}r^2}}{r} \sqrt{g_{1}(r)}+n\frac{{\rm e}^{\frac{\mathbf{s}r^2}{2}}}{r} \sqrt{g_{1}(r)}\Big). \end{aligned} $

(35) Furthermore, the boundary condition of
$ r(x) $ is as follows:$ r\Big(\pm\,\dfrac{L}{2}\Big)=0,\,r(0)=r_{v},\,\, \begin{cases} (\partial_{x}r)^2=\tan^2(\alpha),&r=r_{v}\\ (\partial_{x}r)^2=0,&r=r_{0}. \end{cases} $

(36) The generalized force balance equation at
$ r_{v} $ is the same as for intermediate L. We can use this equation to relate$ r_{v} $ to α. Additionally, we need to find the functional relationship between$ r_{0} $ and$ r_{v} $ due to inflection points. To accomplish this, we can employ the Euler-Lagrange equation and incorporate the action of the string to derive the first integral.$ \mathcal{H}=\frac{w(r)g_{1}(r)}{\sqrt{g_{1}(r)+g_{2}(r)(\partial_{x}r)^2}}, $

(37) $ \mathcal{H} $ is a constant. We bring the boundary conditions to the first integral.$ \mathcal{H}|_{r=r_{v}}=\frac{w(r_{v})g_{1}(r_{v})}{\sqrt{g_{1}(r_{v})+g_{2}(r_{v})\tan^2(\alpha)}}, $

(38) $ \mathcal{H}|_{r=r_{0}}=w(r_{0})\sqrt{g_{1}(r_{0})}. $

(39) Hence, we obtain
$ \partial_{x}r=\sqrt{\frac{w(r)^{2}g_{1}(r)^{2}-g_{1}(r)w(r_{0})^{2}g_{1}(r_{0})}{w(r_{0})^{2}g_{1}(r_{0})g_{2}(r)}}. $

(40) Given that the correspondence between α and
$ r_{v} $ has been established in the generalized force equilibrium equation, we can determine the correspondence between$ r_{0} $ and$ r_{v} $ by using the following relationship:$ w(r_{0})\sqrt{g_{1}(r_{0})}=\frac{w(r_{v})g_{1}(r_{v})}{\sqrt{g_{1}(r_{v})+g_{2}(r_{v})\tan^2(\alpha)}}. $

(41) Furthermore,
$ \partial_{r}x=\dfrac{1}{\partial_{x}r} $ . To simplify the calculations, we can obtain the energy after performing the integral equivalent transformation and renormalization as follows:$ \begin{aligned}[b] E_{QQq}=\;&g\Big(2\int_{0}^{r_{v}} \big(w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}-\frac{1}{r^{2}}\big){\rm d}r\\&+2\int_{r_{v}}^{r_{0}} w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}{\rm d}r\\ &-\frac{2}{r_{v}} +3k\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r} \sqrt{g_{1}(r_{v})}+n\frac{{\rm e}^{\frac{\mathbf{s}r_{v}^2}{2}}}{r_{v}} \sqrt{g_{1}(r_{v})}\Big)+2c. \end{aligned} $

(42) Referring to Fig. 3, the separation distance of the heavy-quark pair L should be:
$ L=2\Big(\int_{0}^{r_{v}}\frac{\partial x}{\partial r} {\rm d}r+\int_{r_{v}}^{r_{0}}\frac{\partial x}{\partial r} {\rm d}r\Big). $

(43) Combining Eqs. (42) and (43), we can obtain the potential energy at large L.
-
At low temperatures and low rapidities,
$ {QQq} $ is confined, and there is an imaginary wall$ r_{w} $ [58−62]. However, as the temperature or rapidity increases,${QQq} $ will also become deconfined. When$ {QQq} $ is confined, the separation distance L and potential energy E will increase with$ r_{v} $ . Furthermore, at a certain point, L will increase sharply until infinity. However, in reality, the separation distance L does not continue to increase infinitely. When the potential energy of${QQq} $ reaches a certain critical point, the string connecting the quarks breaks, which is termed as string breaking. This leads to the excitation of light and anti-light quarks in the vacuum. When the$ {QQq} $ is deconfined, the imaginary wall disappears. As$ r_{v} $ increases, the separation distance reaches a maximum, and simultaneously, the potential energy reaches a maximum at this point. This implies$ {QQq} $ screening at this point.This section examines the properties of
${QQq} $ at finite rapidity based on different research perspectives. It can be divided into three parts. First, it involves analyzing the influence of rapidity on the string breaking of the confined state. Second, it involves investigating the effect of screening when the$ {QQq} $ is deconfined. Finally, it involves conducting a comprehensive comparison with$ {Q\bar{Q}} $ . Additionally, we construct a state diagram of$ {QQq} $ and$ {Q\bar{Q}} $ in the$ T-\eta $ plane to graphically represent their behavior.Based on Eq. (23), we can solve for the light quark position corresponding to
$ (T,\eta) $ . There are two solutions to this equation within the valid interval, and only the smaller solution satisfies our requirements. We consider this equation as a function of$ r_{q} $ with different T and η shown in Fig. 4. We solve for$ r_{q} $ in these cases at$ T=$ 0.1 GeV and obtain the following results:$ \eta=0.3, ~ r_{q}= 1.1487~\mathrm{GeV^{-1}}; ~ \eta=0.6, ~ r_{q}=1.1587~\mathrm{GeV^{-1}}; ~\eta=0.9, ~ r_{q}=1.1823 \mathrm{GeV^{-1}}; ~ \eta=1.3865, ~ r_{q}=1.4582~\mathrm{GeV^{-1}} $ .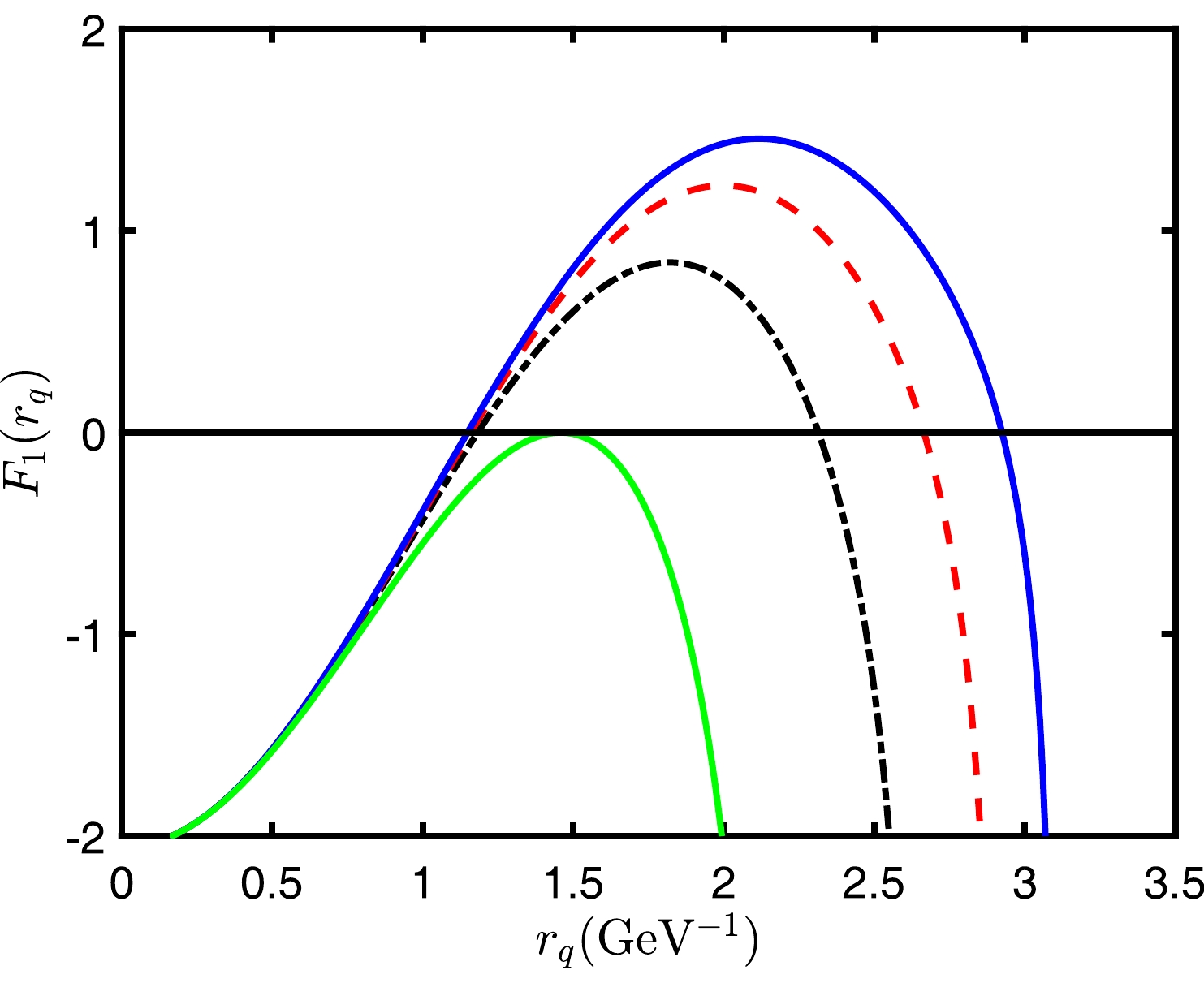
Figure 4. (color online)
$ F_{1} $ as a function of$ r_{q} $ for various rapidities at$ T=0.1\,\mathrm{GeV} $ . The blue line represents$ \eta=0.3 $ , the red dashed line represents$ \eta=0.6 $ , the black dot-dashed line represents$ \eta=0.9 $ , and the green line represents$ \eta=1.3865 $ . Only the green line has one zero point, and the other three lines have two zero points.In Fig. 4, it can be observed that, at a constant temperature, the function
$ F_{1}(r_{q}) $ decreases as the rapidity increases until it no longer has any zero values. For each temperature value, there is a corresponding rapidity that results in the function having exactly one solution. We can obtain solutions by solving the following equations:$ \begin{array}{*{20}{l}} \begin{cases} F_{1}(r_{q},T,\eta )&=0,\\ \dfrac{\partial F_{1}(r_{q},T,\eta)}{\partial r_{q}}&=0. \end{cases} \end{array} $

(44) We calculate the angle at different rapidities using Eq. (24) as a function of
$ r_{v} $ at a temperature of$ T=0.1 \; \mathrm{GeV} $ . The resulting plot is shown in Fig. 5. It is evident that regardless of the parameters, the angles are always greater than zero, and as the rapidity increases, the angle decreases. The transverse axes of the angles all start at zero and end at their respective light quark positions$ r_{q} $ . When the baryon vertex coincides with the light quark, denoted by$ r_{v}=r_{q} $ , it indicates that the configuration has entered the second stage, which corresponds to intermediate L. Subsequently, the light quark and baryon vertex increase together. Specifically, the stage where$ r_{v} < r_{q} $ is referred to as the first stage, termed as small L.
Figure 5. (color online) Relation between the position
$ r_{v} $ of the baryon vertex and angle α, which is between the string and horizon at$ T=0.1\,\mathrm{GeV} $ and various rapidities. Among them, the blue line represents$ \eta=0.3 $ , the red dashed line represents$ \eta=0.6 $ , the black dot-dashed line represents$ \eta=0.9 $ , and the green line represents$ \eta=1.3865 $ .At the intermediate L, we can solve Eq. (30) to obtain the relation between angles α and
$ r_{v} $ . Then, we draw this plot at different rapidities, as shown in Fig. 6. It can be observed that, when the rapidity is small, the angle decreases with$ r_{v} $ linearly, and when it decreases to less than$ 0 $ , we consider that$ {QQq} $ transitions from the second stage to the third stage, which corresponds to large L. Additionally, as the rapidity increases, the angular plot of the second stage changes significantly. The curve of α always moves upwards, does not continue to monotonically decrease, and gradually bends upwards from a straight line to a curve. Hence, ultimately it monotonically increases. Based on these results, when the rapidity is large, the third stage configuration of the model is not possible.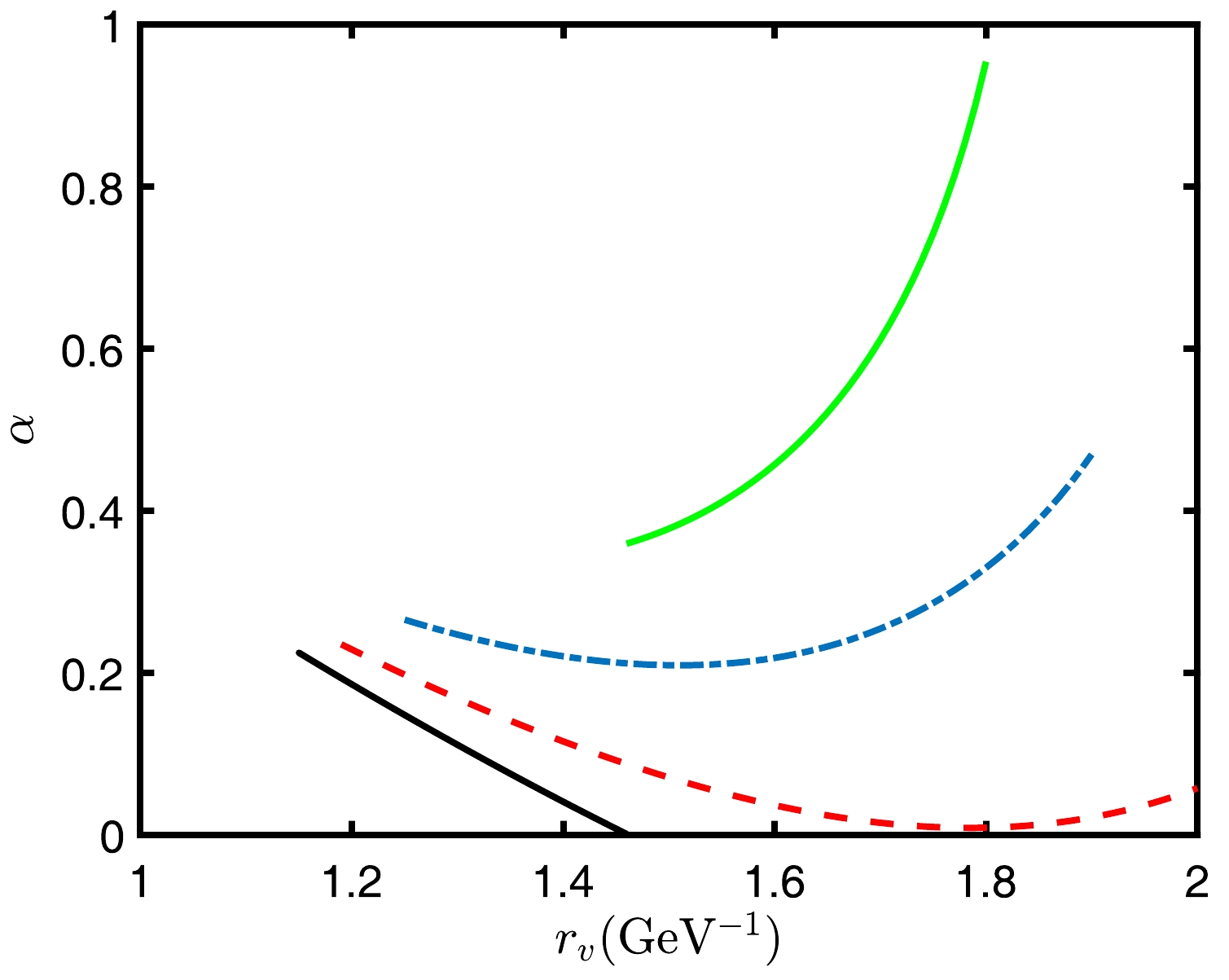
Figure 6. (color online) Relation between the position
$ r_{v} $ of the baryon vertex and angle α, which is between the string and horizontal at$ T=0.1\,\mathrm{GeV} $ and various rapidities. Among them, the black line represents$ \eta=0.3 $ , the red dashed line represents$ \eta=0.9 $ , the blue dot-dashed line represents$ \eta=1.2 $ , and the green line represents$ \eta=1.3865 $ .Figure 7 shows the relation between angles α and the
$ r_{v} $ in the third stage. This result is obtained through Eq. (30). Their transverse axes all start at the end point of their respective second stages, and the longitudinal axes start at$ 0 $ . It can be seen that, as the rapidity increases, the range of configuration in the third stage continues to decrease until it no longer exists. This dovetails with our analysis in the second phase. Since the string configuration features smooth turning points during the third stage, we obtain the relation between$ r_{v} $ and$ r_{0} $ using Eq. (41), as shown in Fig. 8. From the calculated results between α and$ r_{v} $ in each stage, it can be observed that α is smooth between the two stages.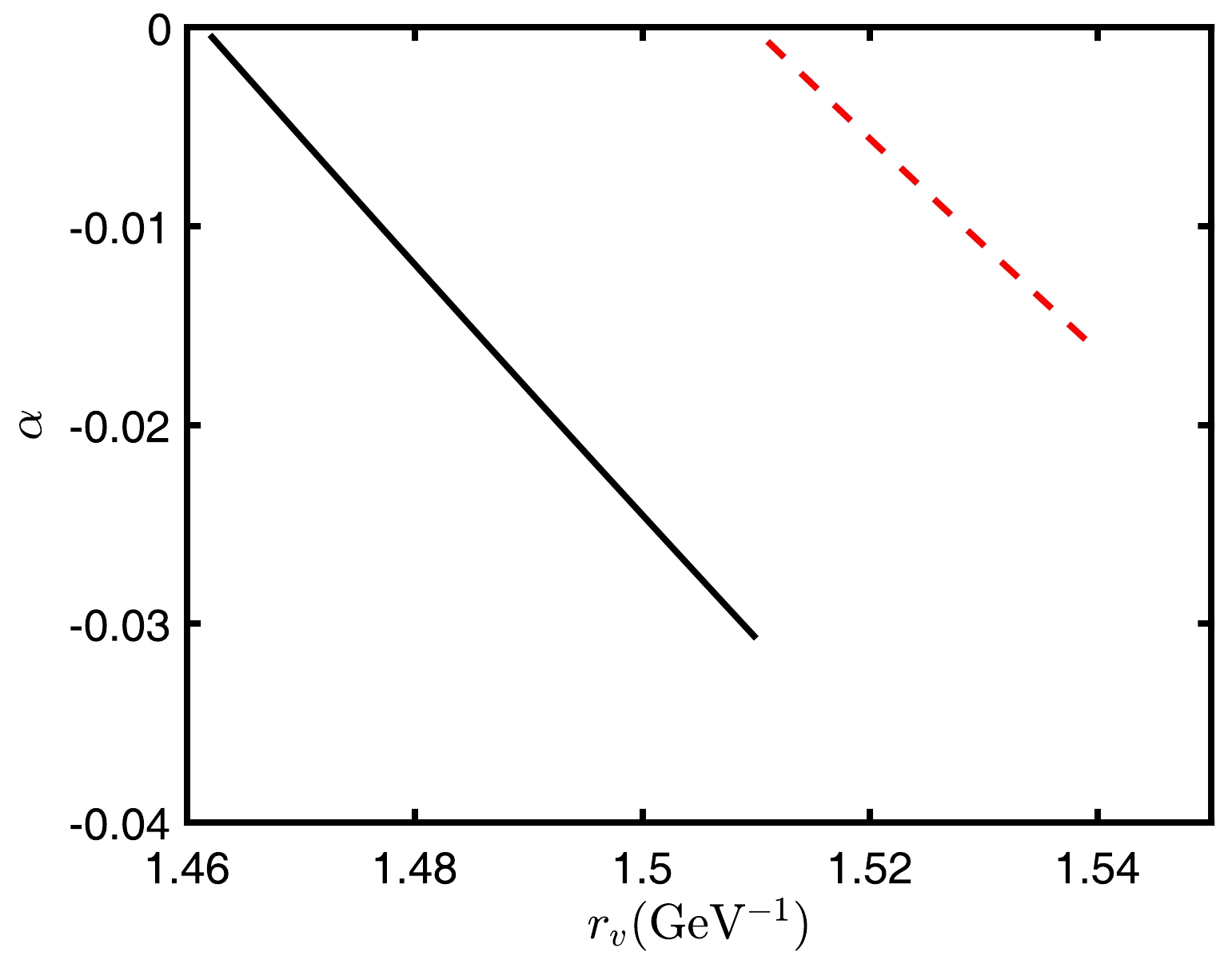
Figure 7. (color online) Relation between the position
$ r_{v} $ of the baryon vertex and angle α, which is between the string and horizontal, at$ T=0.1\,\mathrm{GeV} $ and various rapidities. Among them, the black line represents$ \eta=0.3 $ ; the red dashed line represents$ \eta=0.6 $ .
Figure 8. Relation between the smooth turning point
$ r_{0} $ on the string and position$ r_{v} $ of the baryon vertex at$ T=0.1\,\mathrm{GeV} $ and$ \eta=0.3 $ .In Fig. 9, we present the results of L as a function of
$ r_v $ based on Eqs. (25) and (43). At$ T=0.1\,\mathrm{GeV} $ and$ \eta=0.3 $ , QQq will be confined, and the separation distance can tend to infinity. Subsequently, we use Eqs. (13), (29), and (42) to obtain a plot of E and L as shown in Fig. 10. In the confined state, the potential of$ {QQq} $ is also the Cornell potential with finite temperature and rapidity. -
When
${QQq} $ is confined, string breaking occurs when potential energy E reaches a certain value, exciting positive and negative light quarks in the vacuum. The pattern of string breaking is as follows:$ \begin{array}{*{20}{l}} {QQq} \longrightarrow {Qqq}+{Q\bar{q}}. \end{array} $

(45) The schematic diagram after the string breaking is shown in Fig. 11. It can be observed that the action of
$ {Qqq} $ is provided by three strings, a baryon vertex, and two light quarks. The action of$ {Q\bar{q}} $ comprises a string and light quark. Therefore, the total action after the string breaking is as follows: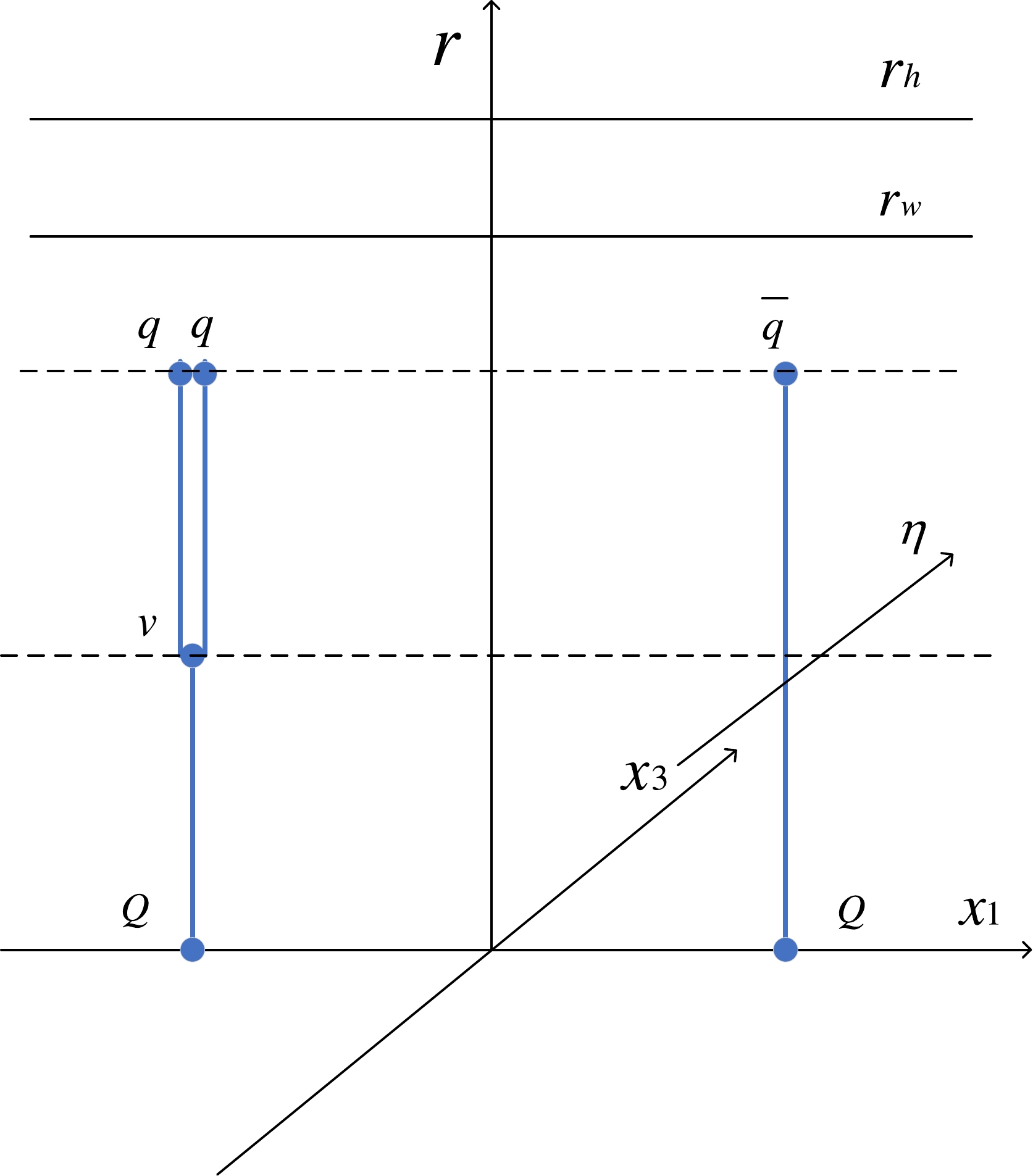
Figure 11. (color online) Schematic diagram after string breaking. Rapidity η is along the
$ x_3 $ -axis direction.$ r_{h} $ denotes the position of the black hole horizon.$ r_{w} $ denotes the position of an imaginary wall when$ {QQq} $ is confined.$ S_{Qqq}=\sum\limits_{i=1}^{3} S_{\rm NG}^{(i)}+S_{\rm vert}+2S_{q}, $

(46) $ S_{Q\bar{q}}=S_{\rm NG}+S_{q}. $

(47) We select the gauge as
$ \xi^{0}=t,\,\xi^{1}=r $ . Therefore, we obtain that the boundary condition of$ x(r) $ is as follows:$ \begin{array}{*{20}{l}} (\partial_{r}x)^2=0. \end{array} $

(48) Hence, the total action can be expressed as
$ \begin{aligned}[b] S=\;>\Big(\int_{0}^{r_{v}}w(r)\sqrt{g_{2}(r)}{\rm d} r+2\int_{r_{v}}^{r_{q}}w(r)\sqrt{g_{2}(r)}{\rm d} r\\&+\int_{0}^{r_{q}}w(r)\sqrt{g_{2}(r)}{\rm d}r\\ &+3k\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}+3n\frac{{\rm e}^{\frac{\mathbf{s}r_{q}^2}{2}}}{r_{q}} \sqrt{g_{1}(r_{q})}\Big). \end{aligned} $

(49) A simple analysis shows that the generalized force equilibrium equation at light quarks does not change after string breaking, i.e., the positions of the three light quarks will be consistent with the one before breaking. However, the force configuration at the baryon vertex of
$ {Qqq} $ changes, and we can denote it as follows:$ F_{2}(r_{v})=\frac{2e_{3}-e_{3}+f_{v}}{gw(r_{v})}=\frac{e_{3}+f_{v}}{gw(r_{v})}=0, $

(50) where
$ e_{3} $ and$ f_{v} $ coincide with Eqs. (19) and (22). There is only one unknown quantity,$ r_{v} $ , in the aforementioned equation, Hence, we can solve for its value. This equation usually solves for two values within the range where$ r_{v} $ has physical significance, and we consider the smaller value here. We solve for$ r_{v} $ in these cases at$ T=0.1\,\,\mathrm{GeV} $ as follows:$\eta=0.3,\,r_{v}=0.4088\,\,\mathrm{GeV^{-1}};$ $\eta= 0.6,\,r_{v}=0.4049\,\mathrm{GeV^{-1}};\, \eta= 0.9,\,r_{v}=0.3987\,\mathrm{GeV^{-1}}$ .Then, we consider the renormalization to determine the potential energy after string breaking:
$ \begin{aligned}[b] E_{\rm break}=\;&g\Big(\int_{0}^{r_{v}}\big(w(r)\sqrt{g_{2}(r)}-\frac{1}{r^{2}}\big){\rm d} r\\&+2\int_{r_{v}}^{r_{q}}w(r)\sqrt{g_{2}(r)}{\rm d}r+\int_{0}^{r_{q}}\big(w(r)\sqrt{g_{2}(r)}-\frac{1}{r^2}\big){\rm d} r\\ &-\frac{1}{r_{v}}-\frac{1}{r_{q}} +3k\frac{{\rm e}^{-2\mathbf{s}r_{v}^2}}{r_{v}} \sqrt{g_{1}(r_{v})}+3n\frac{{\rm e}^{\frac{\mathbf{s}r_{q}^2}{2}}}{r_{q}} \sqrt{g_{1}(r_{q})}\Big)+2c. \end{aligned} $

(51) We calculate the potential energy at
$ T=0.1~\mathrm{GeV} $ after string breaking and obtain the following:$ \eta=0.3,$ $ E_{\rm break}=3.0040~\mathrm{GeV}; ~\eta=0.6,~ E_{\rm break}=2.9983~\mathrm{GeV}; ~ \eta=0.9, E_{\rm break}=2.9857~\mathrm{GeV}$ .The potential energies of
${QQq} $ are shown in Fig. 12. From Fig. 12, it can be observed that a higher rapidity leads to a lower potential energy of$ {QQq} $ . The calculated data are as follows:$\eta=0.3,~L_{\rm break}=1.2812~\mathrm{fm};~\eta=0.6, L_{\rm break}= 1.2874~\mathrm{fm};~\eta=0.9,~ L_{\rm break}=1.3037~\mathrm{fm}$ . Based on these results, we conclude that the string-breaking distance is enhanced and potential energy is decreased in the presence of increased rapidity.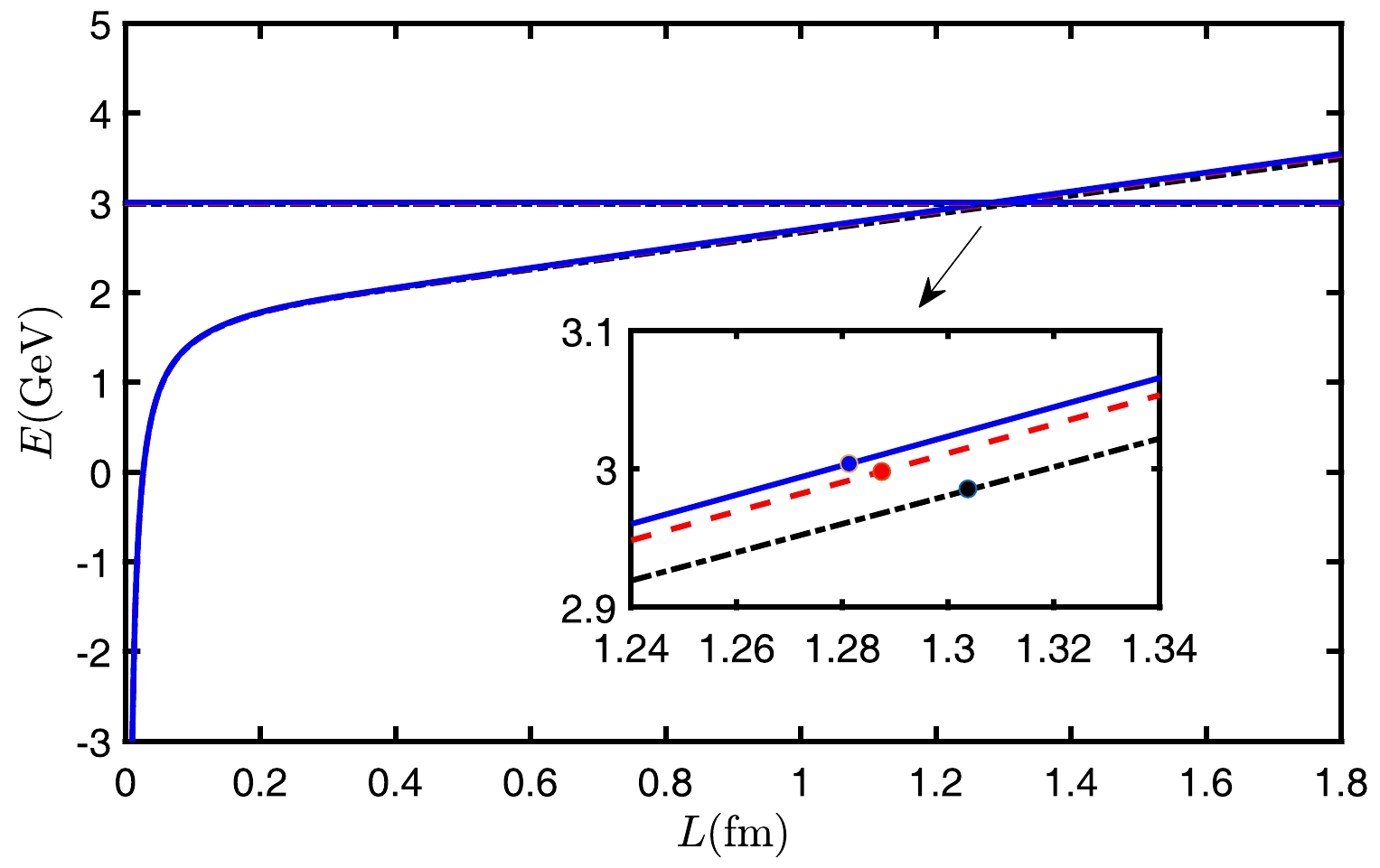
Figure 12. (color online) Curves in the figure are the potential energy of
$ {QQq} $ at$ T=0.1\,\mathrm{GeV} $ , and the straight lines denote the potential energy at$ T=0.1\,\mathrm{GeV} $ after string breaking. The black dot-dashed line represents$ \eta=0.9 $ . The red dashed line represents$ \eta=0.6 $ . The blue solid line represents$ \eta=0.3 $ . -
The confined or deconfined state of the
$ {QQq} $ can be determined by analyzing the plots of$ L-r_{v} $ and the effective string tension. It has been observed that the results obtained from both methods are consistent [61]. We calculate the plots of$ L-r_{v} $ for different rapidities at the same temperature, as shown in Fig. 13. As the separation distance L of the$ {QQq} $ increases, it approaches infinity. In contrast, when it is deconfined, the$ L-r_{v} $ plot has a maximum value. Specifically,$ {QQq} $ will become free quarks above the maximum value.
Figure 13. (color online) Separation distance L between pairs of heavy quarks as a function of the position
$ r_{v} $ of the baryon vertex at$ T=0.1\,\mathrm{GeV} $ . The solid line represents in confined state, while the dashed line represents in deconfined state. The blue line represents$ \eta=0.3 $ , the red line represents$ \eta=0.6 $ , the black line represents$ \eta=0.9 $ , the green line represents$ \eta=1.2 $ , and the yellow line represents$ \eta=1.3865 $ .Figure 13 illustrates the transition of the
$ {QQq} $ from a confined to a deconfined state at a critical rapidity and temperature. When$ {QQq} $ is deconfined, it is observed that, as the rapidity increases, the screening distance and$ r_{v} $ decrease. This implies that, as the rapidity increases,$ {QQq} $ becomes easier to screen. When$ T=0.1\,\mathrm{GeV},\, \eta=1.3865 $ is the maximum rapidity that the$ {QQq} $ model can allow, and its corresponding screening distance is$ L_{\rm melt}=0.4218\,\mathrm{fm} $ . Then,$ r_{v}=1.5682\,\mathrm{GeV^{-1}} $ .We also calculate the plots of E and L as shown in Fig. 14. Based on the figure, it can be observed that the potential energy of the confined
$ {QQq} $ steadily increases with L until string breaking occurs. There is a maximum value for the potential energy of the deconfined state. When E reaches the maximum value, L also reaches the maximum value, which is the apex of L in Fig. 13. As rapidity increases, the potential energy of$ {QQq} $ decreases, and the screening distance becomes smaller. Figure 14 also illustrates that, regardless of whether it is in the confined or deconfined state, as the rapidity increases at a fixed temperature, the potential energy becomes smaller. The calculation results about the screening of$ {QQq} $ in the deconfined state are as follows: at$ \eta =1.2 $ ,$L_{\rm screen}= 0.7304~\mathrm{fm},~ E_{\rm screen}=2.3547~\mathrm{GeV}$ ; at$ \eta =1.3865 $ ,$L_{\rm screen}= 0.4219~\mathrm{fm},~ E_{\rm screen}=2.0317~\mathrm{GeV}$ .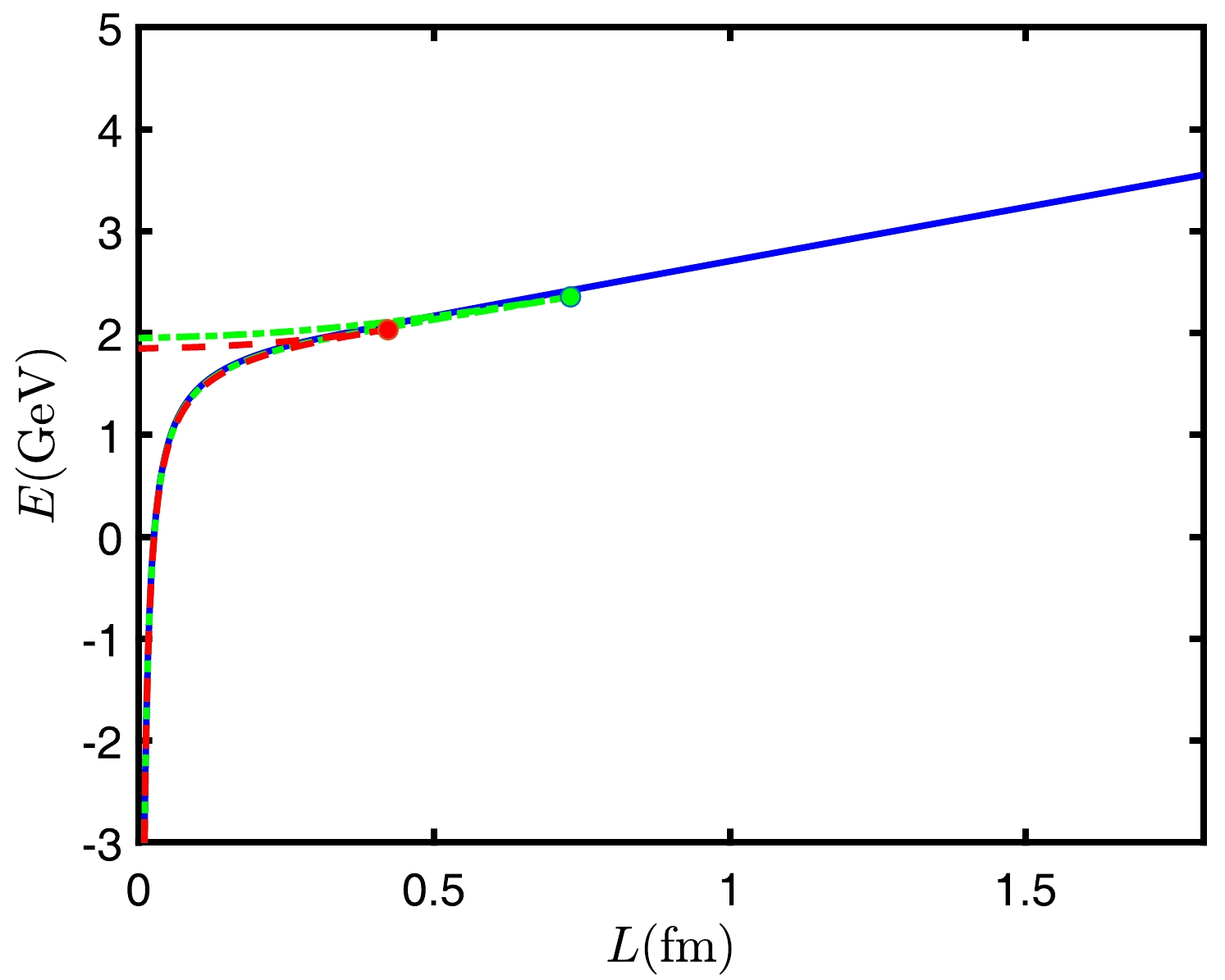
Figure 14. (color online) Relation between the potential energy E and separation distance L at
$ T=0.1\,\mathrm{GeV} $ . The solid line represents a confined state, while the dashed line represents a deconfined state. The solid blue line represents$ \eta =0.3 $ , the green dot-dashed line represents$ \eta =1.2 $ , and the red dashed line represents$ \eta =1.3865 $ .We will briefly introduce the method for determining confined and deconfined states. If the maximum value of the screening distance is smaller than the distance of string breaking, it indicates that
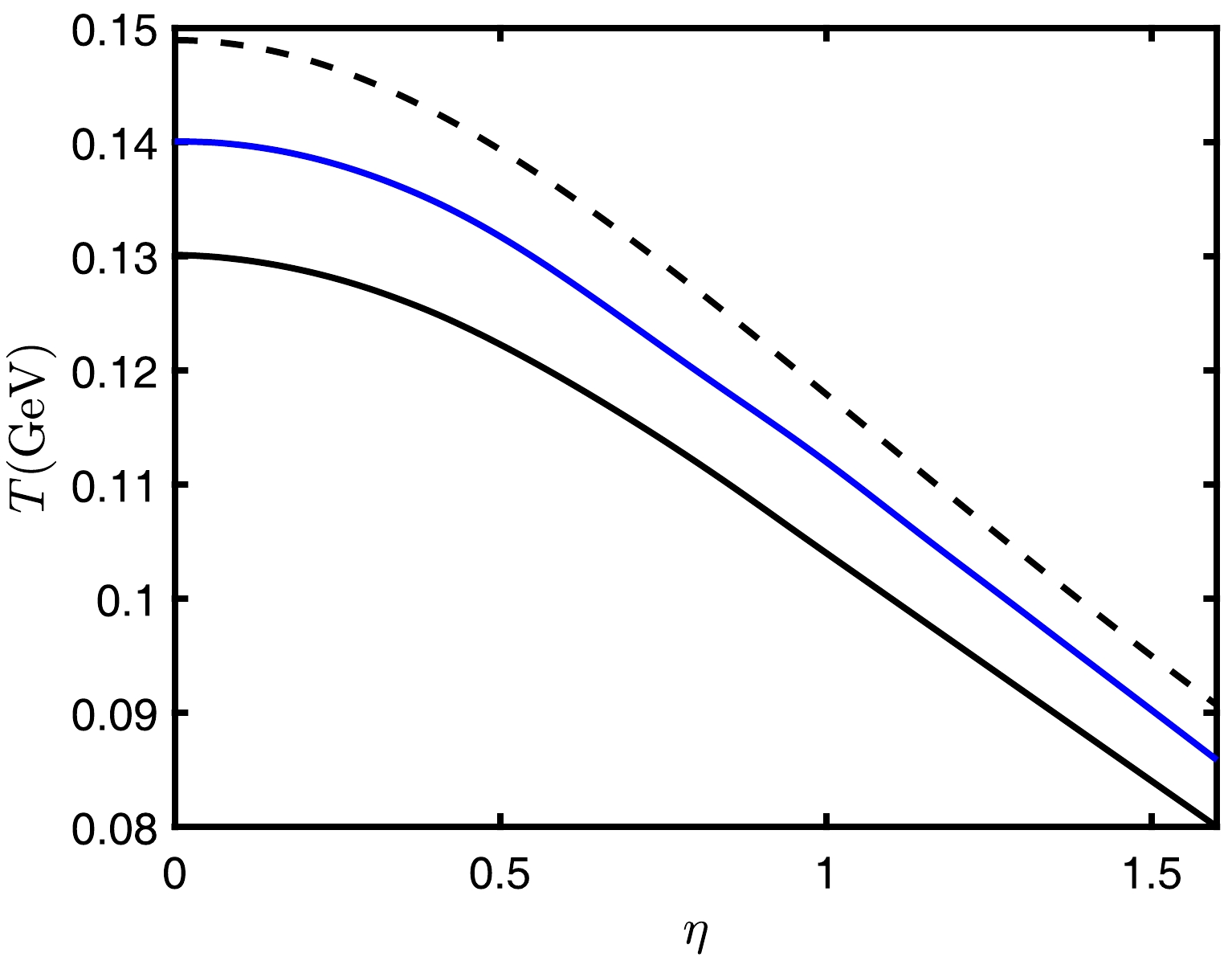
$ {QQq} $ is in the deconfined state; otherwise, it is in the confined state. Using this method, we perform calculations to determine the critical points, and these results are plotted in Fig. 15.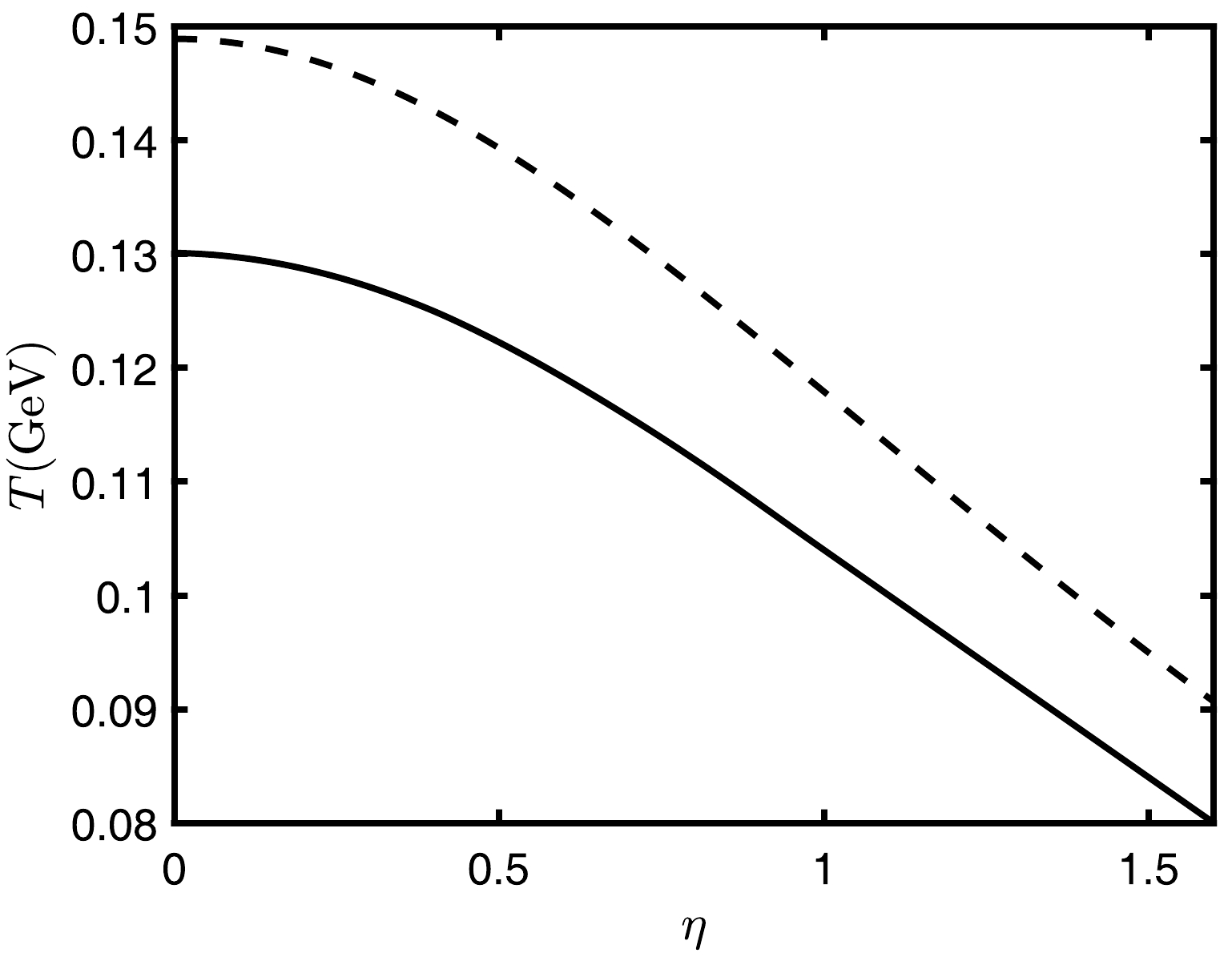
Figure 15. (color online) Dashed line consists of the maximum
$ (\eta,\, T) $ points determined via Eq. (44), and the solid line consists of the critical points that distinguish the confined state from the deconfined state.In Fig. 15,
$ {QQq} $ cannot exist in a medium with temperatures and rapidities above the dashed line. Specifically,${QQq} $ is in the deconfined state between the dashed and solid lines. In this state,$ {QQq} $ become free quarks at long distances due to screening. When$ {QQq} $ is in the deconfined state and the rapidity increases at a fixed temperature, the screening distance decreases. Below the solid line,$ {QQq} $ is in the confined state. In this state, when the separation distance reaches the string-breaking distance and string breaking occurs, it transitions into a new configuration. -
Research on
$ {Q\bar{Q}} $ through holographic models is sufficiently mature [46, 62−69]. We mainly examine the difference between$ {Q\bar{Q}} $ and${QQq} $ under the influence of rapidities.First, we can write the metric after adding the rapidity effect of
$ {Q\bar{Q}} $ through the Lorentz transformation:$ \begin{aligned}[b] {\rm d}s^{2}=\;&w(r)\Big(-g_{1}(r){\rm d}t^{2} -2\sinh(\eta)\cosh(\eta)\big(1-\frac{g_{1}(r)}{g_{2}(r)}\big){\rm d}x_{3}{\rm d}t\\ &+g_{3}(r){\rm d}x_{3}^{2}+{\rm d}x_{1}^{2}+{\rm d}x_{2}^{2}+\frac{g_{2}(r)}{g_{1}(r)}{\rm d}r^{2}\Big),\\[-14pt] \end{aligned} $

(52) where
$ w(r),\,g_{1}(r),\,g_{2}(r), $ and$ \,g_{3}(r) $ are consistent with the previously derived Eqs. (2) and (5).We select the static gauge
$ \xi^{0}=t $ ,$ \xi^{1}=x $ , and the action of$ {Q\bar{Q}} $ can be expressed as$ \begin{aligned}[b] S=\;>\Big(\int_{-\frac{L}{2}}^{0} w(r)\sqrt{g_{1}(r)+g_{2}(r)(\partial_{x}r)^2} {\rm d}x\\&+\int_{0}^{\frac{L}{2}} w(r)\sqrt{g_{1}(r)+g_{2}(r)(\partial_{x}r)^2}\Big){\rm d}x. \end{aligned} $

(53) Furthermore, the boundary condition of
$ r(x) $ is as follows:$ r\Big(\pm\,\frac{L}{2}\Big)=0,~~r(0)=r_{0},~~(\partial_{x}r|_{r=r_{0}})^2=0. $

(54) The string configuration of
$ {Q\bar{Q}} $ is U-shaped, where$ r_{0} $ denotes the smooth turning point of the U-shaped string. With the Euler-Lagrange equation, we obtain the following:$ \partial_{x}r=\sqrt{\frac{w(r)^{2}g_{1}(r)^{2}-g_{1}(r)w(r_{0})^{2}g_{1}(r_{0})}{w(r_{0})^{2}g_{1}(r_{0})g_{2}(r)}}. $

(55) By renormalizing, we can obtain the potential energy of
${Q\bar{Q}} $ as follows:$ \begin{aligned}[b] E_{Q\bar{Q}}=\;&g\Big(2\int_{0}^{r_{0}} \big(w(r)\sqrt{g_{1}(r)(\partial_{r}x)^2+g_{2}(r)}-\frac{1}{r^{2}}\big){\rm d}r\\&-\frac{2}{r_{0}}\Big)+2c. \end{aligned} $

(56) Furthermore,
$ L=2\int_{0}^{r_{0}}\frac{\partial x}{\partial r} {\rm d} r, $

(57) where
$ \partial_{r}x=\dfrac{\partial x}{\partial r}=\dfrac{1}{\partial_{x}r} $ .We can calculate the potential energy of
$ {Q\bar{Q}} $ at different rapidities at the same temperature and compare it with$ {QQq} $ . The result is presented in Fig. 16, indicating that the potential energy of$ {QQq} $ is higher than that of${Q\bar{Q}} $ . Furthermore, it is observed that increasing rapidity consistently leads to a decrease in the potential energy of$ {Q\bar{Q}} $ and${QQq} $ . When$ {Q\bar{Q}} $ is in the confined state, the$ {Q\bar{Q}} $ string breaks when the separation distance becomes sufficiently large. Let us consider the pattern of$ {Q\bar{Q}} $ string breaking as
Figure 16. (color online) Potential energies of
${Q\bar{Q}} $ and$ {QQq} $ are depicted at$ T=0.1\,\mathrm{GeV} $ . In the graph, the black dot-dashed line represents$ \eta=0.9 $ , the red dashed line represents$ \eta=0.6 $ , and the blue solid line represents$ \eta=0.3 $ .$ \begin{array}{*{20}{l}} {Q\bar{Q}} \longrightarrow {Q\bar{q}}+ {\bar{Q}q}. \end{array} $

(58) Evidently,
$ \begin{aligned}[b] E_{break}=\;&2g\Big(\int_{0}^{r_{q}}\big(w(r)\sqrt{g_{2}(r)}-\frac{1}{r^2}\big){\rm d}r\\&-\frac{1}{r_{q}}+n\frac{{\rm e}^{\frac{sr_{q}^2}{2}}}{r_{q}} \sqrt{g_{1}(r_{q})}\Big)+2c. \end{aligned} $

(59) Based on this, we can generate the plot in Fig. 17. As shown in the figure, it is evident that increasing rapidity leads to a greater separation distance at the point of string breaking for both
$ {Q\bar{Q}} $ and$ {QQq} $ . The calculated data are$\eta=0.3, E_{\rm break}=2.3906~\mathrm{GeV},\, L_{\rm break}=1.2331~\mathrm{fm};\,\eta=0.6,$ $E_{\rm break}\,= 2.3868\;\,\mathrm{GeV},~\,\, L_{\rm break}=1.2382~\,\mathrm{fm};\,\, ~\eta=0.9,~\,\, E_{\rm break}= $ $2.3784~\mathrm{GeV}, L_{\rm break}=1.2474~\mathrm{fm} $ . It can be observed that the breaking distance of$ {Q\bar{Q}} $ is slightly less than$ {QQq} $ . However, the difference between the two is not significant.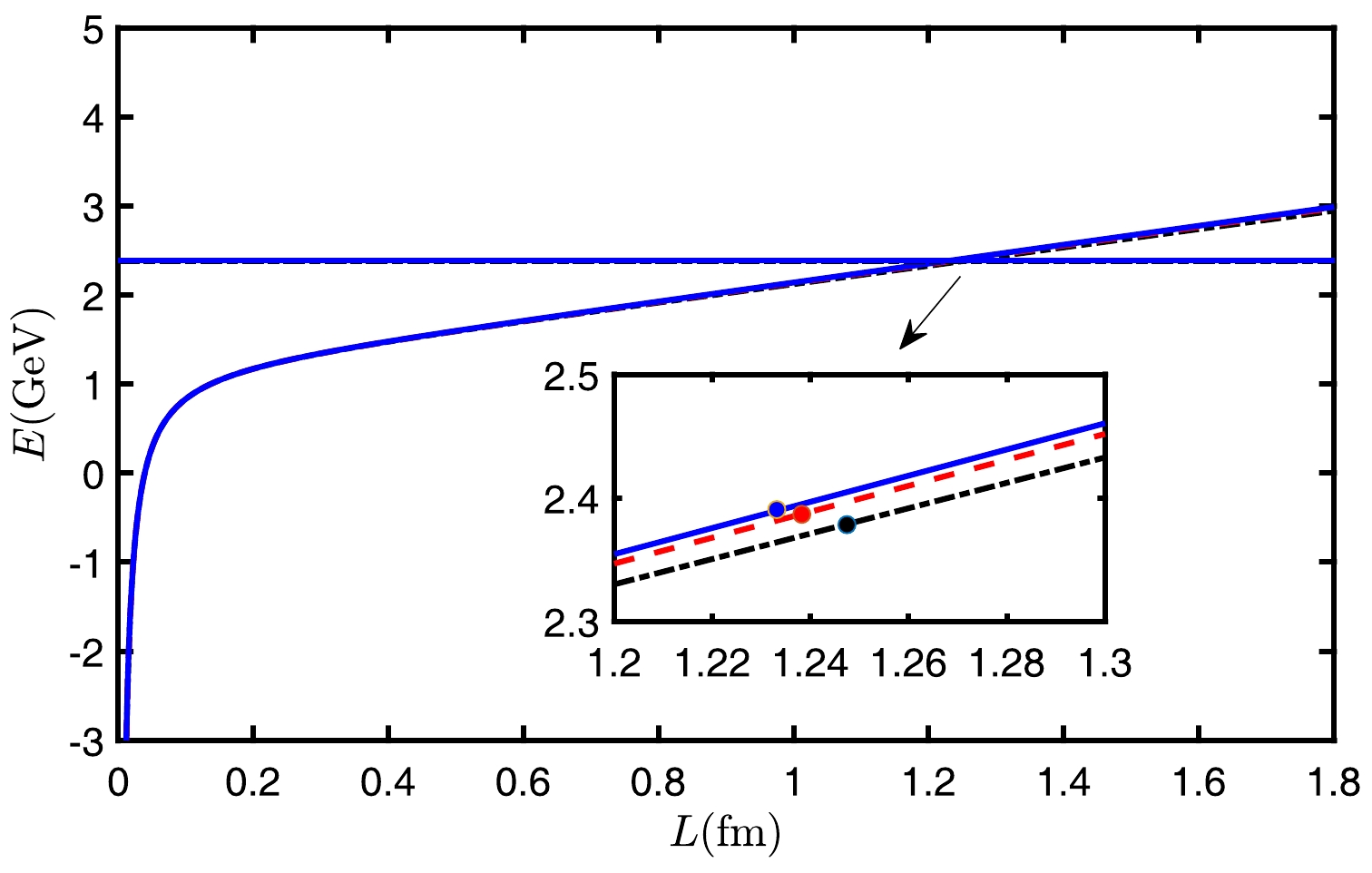
Figure 17. (color online) Curves in the figure are the potential energy of
$ {Q\bar{Q}} $ at$ T=0.1\,\mathrm{GeV} $ , and the straight lines are the potential energy at$ T=0.1\,\mathrm{GeV} $ after string breaking. Where the black dot-dashed line represents$ \eta=0.9 $ , the red dashed line represents$ \eta=0.6 $ , and the blue solid line represents$ \eta=0.3 $ .When the rapidity continues to increase,
$ {Q\bar{Q}} $ will also change from the confined state to the deconfined state. For this purpose, we calculated the results in Fig. 18. When we calculated the potential of$ {QQq} $ at$ \eta =1.3865 $ and$ T = 0.1 $ GeV, the results show$L_{\rm melt}=0.4219$ fm and$E_{\rm melt}=2.0317$ GeV. When$ {Q\bar{Q}} $ is at$ \eta =1.3865 $ and$ T = 0.1 $ GeV, we obtain$L_{\rm melt}=0.8944\;\mathrm{fm}$ and$E_{\rm melt}= 1.9640$ GeV. It can be observed that the difference in screening distances is significant. We infer that$ {Q\bar{Q}} $ is more stable than$ {QQq} $ at the same temperature and rapidity.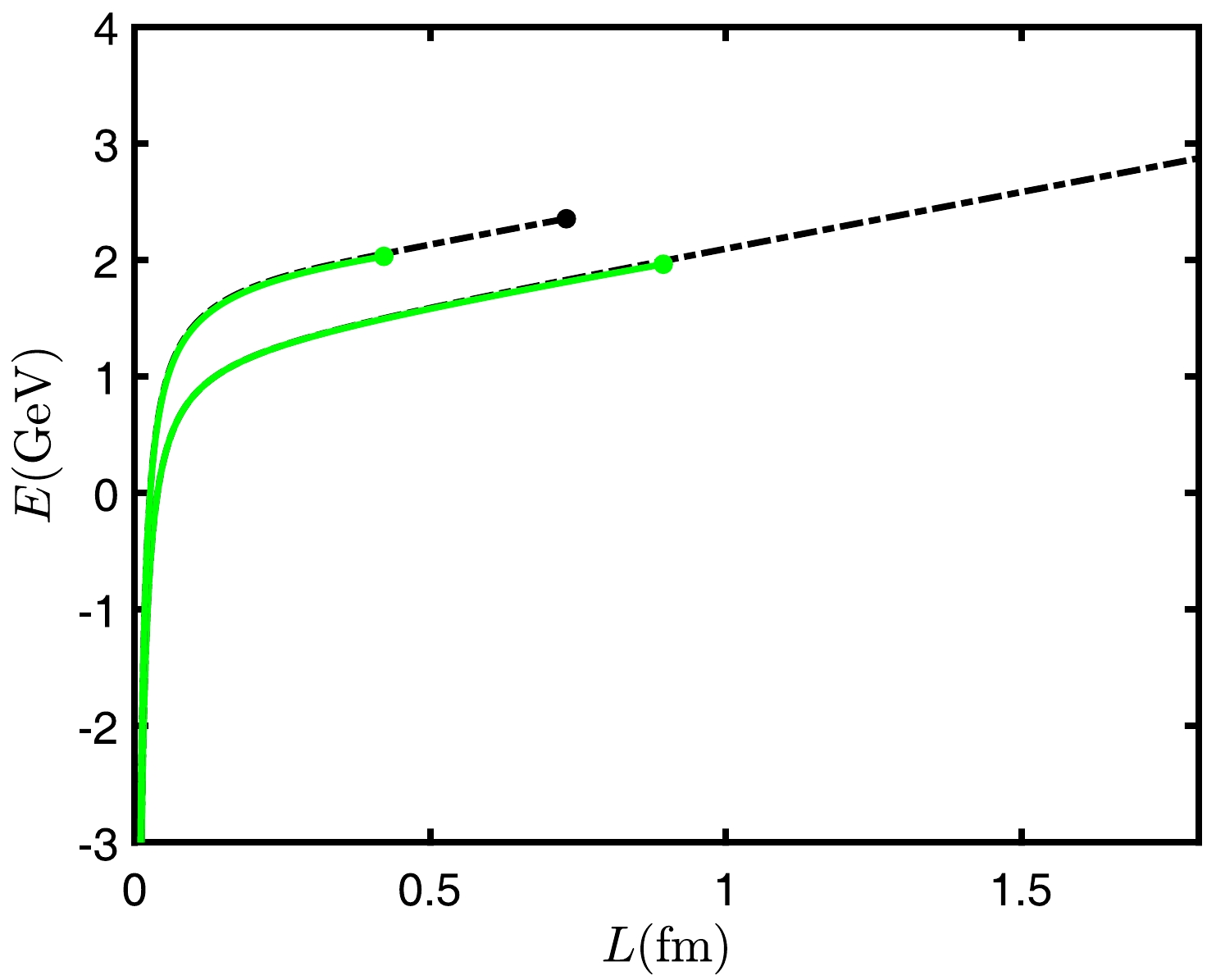
Figure 18. (color online) Higher curves represent
${QQq} $ , and the lower curves represent${Q\bar{Q}} $ . The black line represents$ \eta=1.2,\,T=0.1\,\mathrm{GeV} $ , and the green line represents$\eta=1.3865, $ $ T=0.1\;\mathrm{GeV}$ .Figure 19 shows that
${QQq} $ is confined below the black line, which implies that the separation distance of heavy quarks can be infinite if we ignore the string breaking.$ {QQq} $ can still be found below the black dashed line even when$ {QQq} $ is in the deconfined state. This implies that${QQq} $ can screen at a certain distance. Furthermore,$ {QQq} $ cannot be found anymore above the dashed line. As a comparison, we show$ Q\bar{Q} $ in the same figure with a blue line. The situation differs for$ Q\bar{Q} $ . Additionally,$ Q\bar{Q} $ is confined below the blue line. Above the blue line,$ Q\bar{Q} $ is deconfined. However, we can still find$ Q\bar{Q} $ at any conditions because it can still exist at a small separation distance. -
In this paper, we mainly discuss the properties of
$ {QQq} $ in some aspects at finite temperature and rapidity using the 5-dimensional effective string model for the first time. When$ {QQq} $ is in the confined state, it can undergo string breaking at a large separation distance. We consider the breaking mode to be$ {QQq} \longrightarrow {Qqq}+{Q\bar{q}} $ and observe that higher rapidities make the string breaking more difficult to occur. Under high temperature and rapidity conditions,$ {QQq} $ transitions into the deconfined state. In this state, it becomes the free quarks if the separation distance is larger than the screening distance, and color screening becomes easier with increasing rapidity. Using potential analysis, we constructed a state diagram for$ {QQq} $ in the$ T-\eta $ plane to differentiate between the confined and deconfined states.We compared the properties of
${QQq} $ and$ {Q\bar{Q}} $ . As expected, the potential energy of$ {QQq} $ is always greater than that of${Q\bar{Q}} $ , and the qualitative effects of temperature and rapidity on$ {QQq} $ and${Q\bar{Q}} $ are consistent. In the confined state, it is determined that the string-breaking distance of$ {QQq} $ and$ {Q\bar{Q}} $ are very close. This implies that the sizes of the different hadrons are potentially similar. In the deconfined state, there is a significant difference in the screening distance between$ {QQq} $ and${Q\bar{Q}} $ . It is determined that the screening distance of${QQq} $ is smaller than that of${Q\bar{Q}} $ under the same conditions, which indicates$ {QQq} $ is less stable than${Q\bar{Q}} $ . Furthermore, an interesting result shows that$ {QQq} $ cannot be found above certain temperatures and rapidities. However,$ {Q\bar{Q}} $ can be found at any temperature and rapidity as long as the separation distances are sufficiently small. This study mainly focuses on qualitative analysis and can be extended to yield more accurate results in the future.
Moving doubly heavy baryon in a strongly coupled plasma via holography
- Received Date: 2024-01-29
- Available Online: 2024-08-15
Abstract: Gauge/gravity duality is used to study the properties of the doubly heavy baryon






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: