-
The research on the ground properties of superheavy nuclei is important in nuclear physics. Uranium is the last element with a nearly stable isotope owing to its relatively longer half-life and unique nuclear properties; thus, its use is critical in several fields including nuclear energy [1−3] and astrophysics [4, 5] and in the study of nuclear matter under extreme conditions [6−8]. In superheavy nuclei, the shape of the ground state is no longer spherical. Increasing evidence from experimental [9−14] and nuclear theory research [15−23] shows that not only quadrupole but also reflection-asymmetric or octupole deformations are prevalent, especially in the ground states of actinide nuclei.
In 1995, octupole deformation was first studied in the relativistic mean-field model [24]. The study investigated the occurrence of stable octupolar deformation in the ground states of Ra isotopes and revealed that the mean-field force in use was very sensitive to the transition point from symmetric to asymmetric forms. More systematic studies of octupole deformed nuclei have subsequently been carried out using the macroscopic+microscopic (MM) approach [25] and non-relativistic Hartree-Fock-Bogoliubov (HFB) theories with the Gogny force [17]. By 2016, a global search for octupole deformation was performed using covariant density functional theory [26]. Researchers used five of the most recent covariant energy density functionals, DD-PC1 [27], NL3* [28], DD-ME2 [29], PC-PK1 [30], and DD-MEδ [31], with separable pairing interaction (TMR) [32, 33] to study the octupole deformation in the ground states of even-even nuclei. According to their conclusion, DD-ME2 with TMR pairing interaction can correctly predict the islands of octupole deformation and is in general agreement with the available experimental data.
All the microscopic calculations are based on the even-even nuclei. In a recent study [34], based on the deformed relativistic Hartree-Bogoliubov theory in the continuum (DRHBc), an automatic blocking procedure was adopted in which the orbital with the lowest quasiparticle energy was blocked during the iteration. Compared with the results of orbital-fixed blocking calculations, the computational cost was considerably reduced.
In this study, the relativistic Hartree-Bogoliubov (RHB) theory with multiple deformation constraint including the blocking effect based on the density-dependent functional (DD-ME2) and separable pairing interaction (TMR) is extended to describe the ground state of uranium isotopes from 225 to 240 for both even-even and odd-A nuclei. The theoretical framework is presented in Sec. II. The ground state properties of U isotopes are calculated using the RHB theory and compared with experimental data and Hartree-Fock-Bogoliubov calculations with Gogny D1S in Sec. III. A summary and discussion are presented in Sec. IV.
-
The covariant density functional theory (CDFT) has proven to be a powerful theory in nuclear physics and has gained wide attention in recent years for its many attractive advantages such as the automatic inclusion of nucleonic spin degree of freedom and spin-orbital interaction [35], explanation of pseudospin symmetry in nucleon spectra [36, 37] and spin symmetry in anti-nucleon spectra [38], and natural inclusion of nuclear magnetism [39]. Based on the CDFT and including pairing correlations, the relativistic Hartree-Bogoliubov (RHB) theory was developed in 1996 [40]. After nearly 30 years of development, RHB has achieved great success in describing both stable and exotic nuclei [32, 33, 41−45]. Very recently, the first nuclear mass table including the continuum effect was constructed based on the RHB theory [34, 46], and the blocking effect was considered to study the ground state of odd-A and odd-odd nuclei.
The details of the RHB theory can be found in Refs. [40, 47]. Here, a brief introduction is presented in Sec. II.A, and the blocking procedure is introduced in Sec. II.B.
-
In the RHB framework, quasiparticle wave functions U and V are determined by the RHB equations [47]
$ \left( \begin{array}{cc} \hat{h}_{D}-\lambda & \hat{\Delta} \\ -\hat{\Delta}^* & -\hat{h}_{D}+\lambda \end{array} \right ) \left( \begin{array}{l} U_{k} \\ V_{k} \end{array} \right ) =E_{k}\left( \begin{array}{l} U_{k} \\ V_{k} \end{array} \right ), $

(1) where
$ \hat{h}_{D} $ is the Dirac Hamiltonian, λ is the Fermi energy,$ \hat{\Delta} $ is the pairing potential, and$ E_k $ is the quasiparticle energy.$ \hat{h}_{D}= \frac{\delta E}{\delta \rho}=\pmb{\alpha}\cdot\pmb{p}+V(\pmb{r})+\beta(M-S(\pmb{r})), $

(2) where M is the nucleon mass, and
$ S(\pmb{r}) $ and$ V(\pmb{r}) $ are the scalar and vector potentials, respectively. In this study, we adopted the density-dependent meson-nucleon coupling model (DD-ME2) [29].The pairing field can be written as
$ \Delta = \frac{\delta E}{\delta \kappa}=\frac{1}{2}\sum V^{pp}\kappa . $

(3) Here, we utilize a separable force form in our treatment of forces [45]. This conversion from momentum space to coordinate space enables a more comprehensive understanding of the role of forces in the calculations.
$ V(r_{1}, r_{2}, r'_{1}, r'_{2})= -G \delta(\pmb{R-R'})P(r)P(r')\frac{1}{2}(1-P^{\sigma}). $

(4) In this equation,
$ \pmb{R=(r_{1}+r_{2})}/2 $ and$ \pmb{r=r_{1}-r_{2}} $ are the center of mass and relative coordinates.$ P(r) $ is expressed in the separable form of Gaussian shape$ P(r)=\frac{1}{(4\pi a^{2})^{3/2}}{\rm e}^{-r^{2}/4a^{2}}. $

(5) In order to include the axial reflection asymmetric deformation, the calculation of the RHB function is modified to
$ E_{RHB}+\sum\limits_{i=2,3}[C_{i0}(\langle\hat{Q}_{i0}\rangle-q_{i0})^2+\lambda_{i0}(\langle\hat{Q}_{i0}\rangle-q_{i0})] $

(6) employing the method of augmented Lagrangian [48]. Here,
$ E_{\rm RHB} $ is the total energy,$ \langle\hat{Q}_{20}\rangle $ and$ \langle\hat{Q}_{30}\rangle $ are the expectation values of the quadrupole and octupole moment$ \hat{Q}_{20} = 2z^2-x^2-y^2 ,$

(7) $ \hat{Q}_{30} = z(2z^2-3x^2-3y^2), $

(8) $ q_{i0} $ represents the value of the quadrupole and octupole moment for constraint calculation.$ C_{i0} $ and$ \lambda_{i0} $ are the corresponding stiffness constants and the vector of Lagrange multipliters (additional details about$ \lambda_{i0} $ available in Ref. [48]). When$ \langle\hat{Q}_{i0}\rangle=q_{i0} $ , the final result under the constraint of a certain deformation point will be output. For convenience, we convert$ Q_{20} $ and$ Q_{30} $ to$ \beta_2 $ and$ \beta_3 $ , where$ R_{0}=1.2A^{1/3} $ .$ Q_{20} = \sqrt{\frac{16\pi}{5}}\frac{3}{4\pi}ZR^{2}_{0}\beta_{2}, $

(9) $ Q_{30} = \sqrt{\frac{16\pi}{7}}\frac{3}{4\pi}ZR^{3}_{0}\beta_{3}. $

(10) -
In order to calculate the odd-A or odd-odd nuclei, the blocking effect of the unpaired nucleon should be considered. For the ground state of the even-even system,
$ |\Phi\rangle $ is the vacuum state of the quasiparticle operator.$ \alpha_{k}|\Phi\rangle=0 , $

(11) $ \alpha_{k}^{\dagger} = \sum\limits_{k>0} U_{mk}c^{\dagger}_{m}+V_{mk}c_{m}, $

(12) where
$ U_{mk} $ and$ V_{mk} $ are the Hartree Bogoliubov coefficient, at which point the single particle density and pair tensor can be written as$ \rho =V^{*}V^{T}, $

(13) $ \kappa=V^{*}U^{T}, $

(14) and the one-quasiparticle state for an odd-mass nucleus or odd-odd nucleus is
$ |\Phi_1\rangle=\alpha_{k}^{\dagger}|\Phi\rangle. $

(15) Thus, we can achieve the blocking effect through the conversion between
$ \alpha_{k} $ and$ \alpha_{k}^{\dagger} $ . Thus, the density matrix and pairing tensor are replaced by [34]$ \rho '=\rho +\frac{1}{2}(U_{kb}U_{kb}^{*T}-V_{kb}^{*}V_{kb}^{T}), $

(16) $ \kappa '=\kappa +\frac{1}{2}(U_{kb}V_{kb}^{*T}-V_{kb}^{*}U_{kb}^{T}).$

(17) In order to determine the ground state of an odd-A or odd-odd nucleus, it is crucial to identify the correct deformation minimum and the orbital that needs to be blocked. In the spherical case, we can perform calculations by blocking orbitals individually near the Fermi surface. In the deformed case, many more orbitals are close to the Fermi surface than those in the spherical case. Moreover, if we want to calculate the potential energy surface (PES) of the odd-A or odd-odd nuclei, the computational cost of the orbital-fixed blocking calculation will be extremely high. To enhance computational efficiency, it is crucial to implement an automatic blocking method. One possible blocking procedure for obtaining the ground state of an odd-A or odd-odd nucleus involves blocking the lowest quasiparticle orbital(s) in each iteration, as introduced in Ref. [34].
-
In this section, the ground state properties of U-isotopes, including the PES, binding energy, and three-point pairing interaction are calculated by RHB with the density-dependent meson coupling parameters set (DD-ME2) and separable paring interaction.
-
In this section, we perform the two-dimensional
$ (\beta_2, \beta_3) $ constrained calculations for the U-isotopes from$ ^{225} $ U to$ ^{240} $ U. In Figs. 1−4, we display the PES of U isotopes from$ ^{225} $ U to$ ^{232} $ U in the$ (\beta_2, \beta_3) $ plane from RHB calculations. The two-dimensional constrained method uses Eqs. (7) and (8). All these calculations use$ N_f=20 $ shells. The RHB equations are solved for each point on the deformation lattice$ (\beta_2, \beta_3) $ , in which both$ \beta_2 $ and$ \beta_3 $ run from$ 0.0 $ to$ 0.5 $ with a step of$ 0.025 $ . This deformation lattice covers the shape space of the ground state of all the U-isotopes. The odd-A nuclei are calculated with the automatic blocking procedure.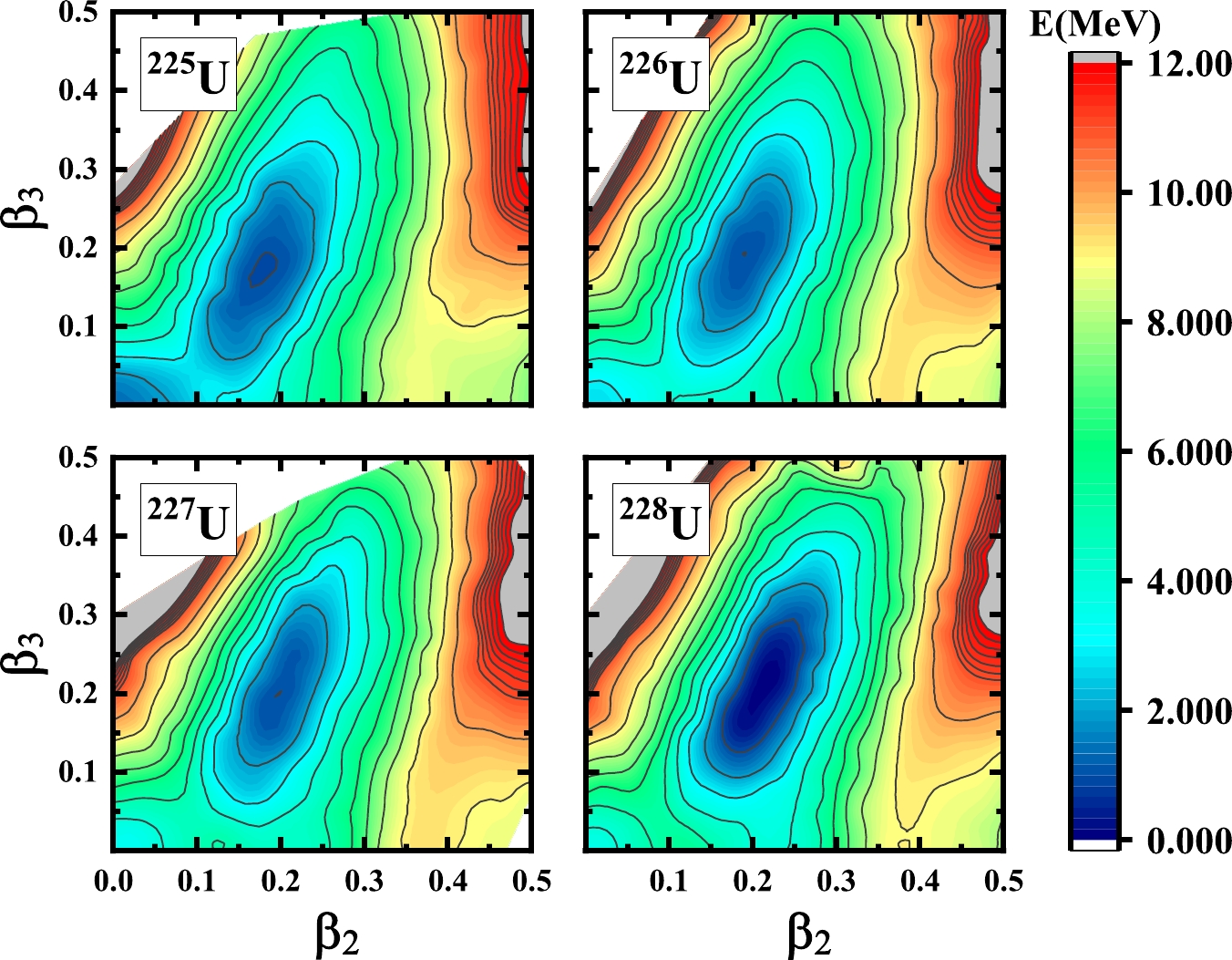
Figure 1. (color online) Potential energy surface (PES) of U isotopes from
$ ^{225} $ U to$ ^{228} $ U in the$ (\beta_2, \beta_3) $ plane from RHB calculations.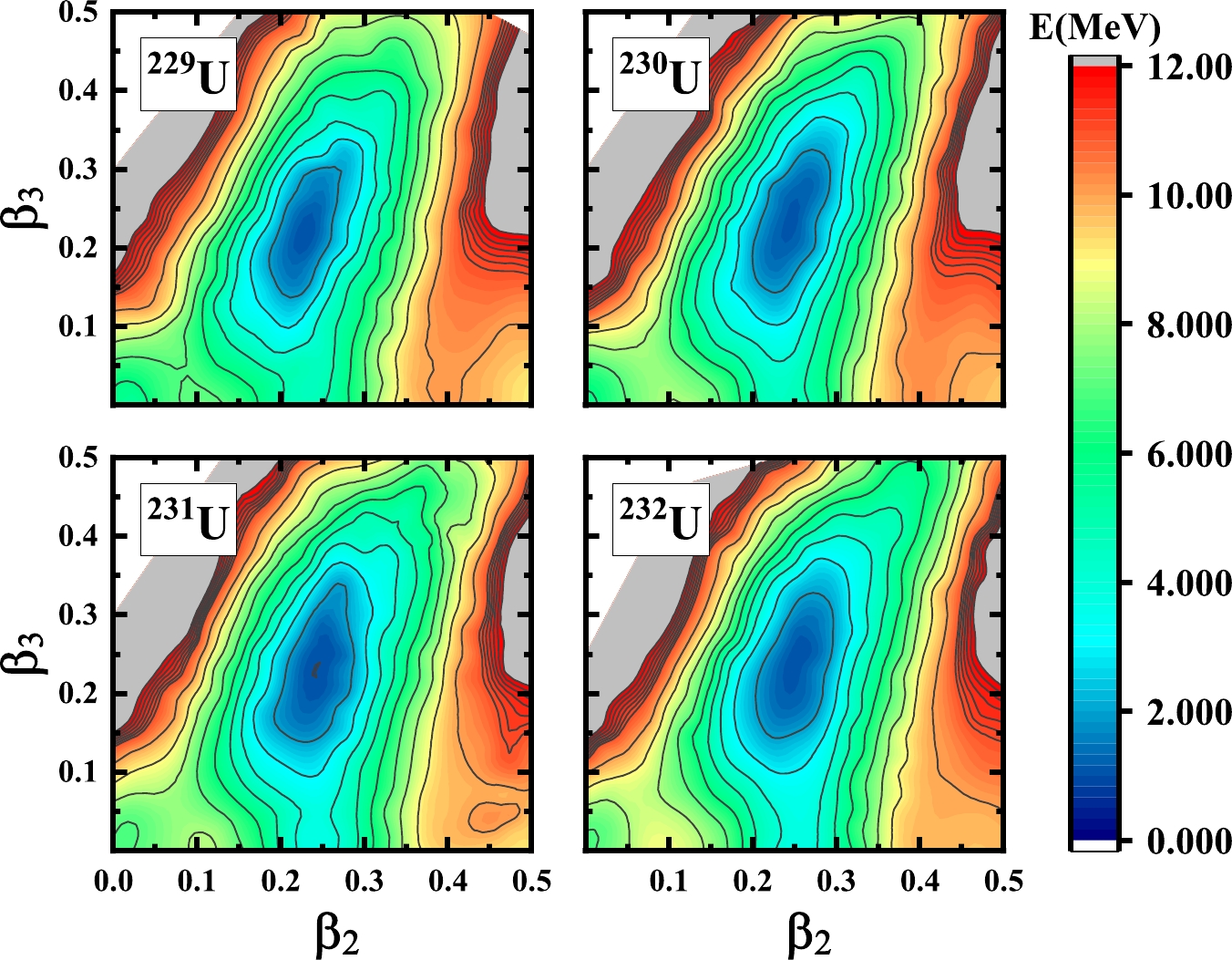
Figure 2. (color online) Same as described in the caption to Fig. 1 but for isotopes
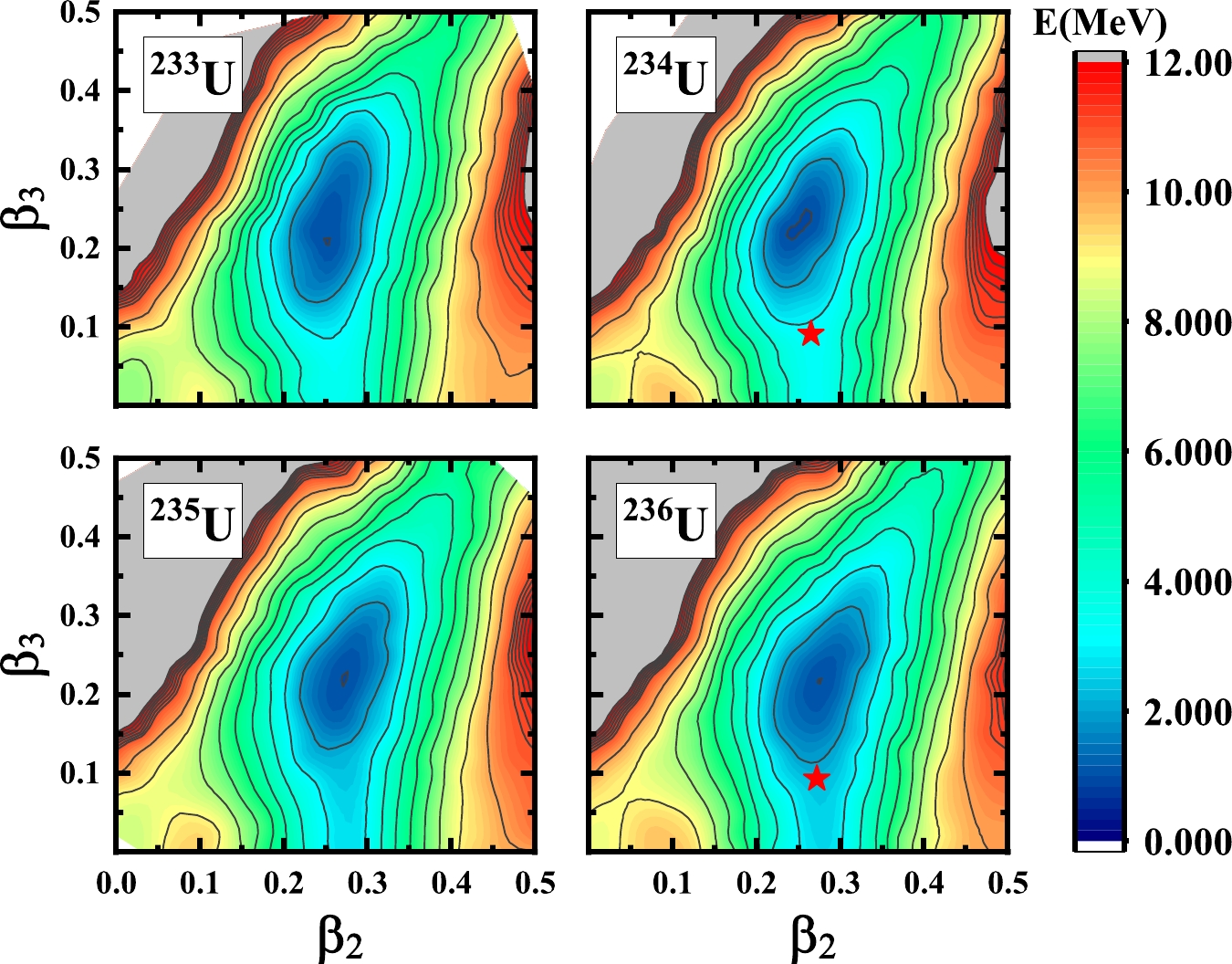
$ ^{229} $ U to$ ^{232} $ U.As we can see in Figs. 1−4, the ground states of most of the U isotopes have the reflection asymmetric deformation minimum. The red pentagrams in the PES of
$ ^{234} $ U,$ ^{236} $ U, and$ ^{238} $ U represent the experimental measurement deformation of the ground state point [9]. For the light nuclei$ ^{225} $ U, since the neutron number is close to the magic number$ 126 $ , there are two minimums of the ground state. One is the spherical case, the other is the well deformed case. Moreover, for the rest of the nuclei, the ground state with the octupole deformation is preferred. Although the PESs of the ground states for$ ^{239} $ U and$ ^{240} $ U become very flat, the ground states of these nuclei with the octupole deformation are still preferred. -
We obtained the ground state binding energies of the U isotopes from
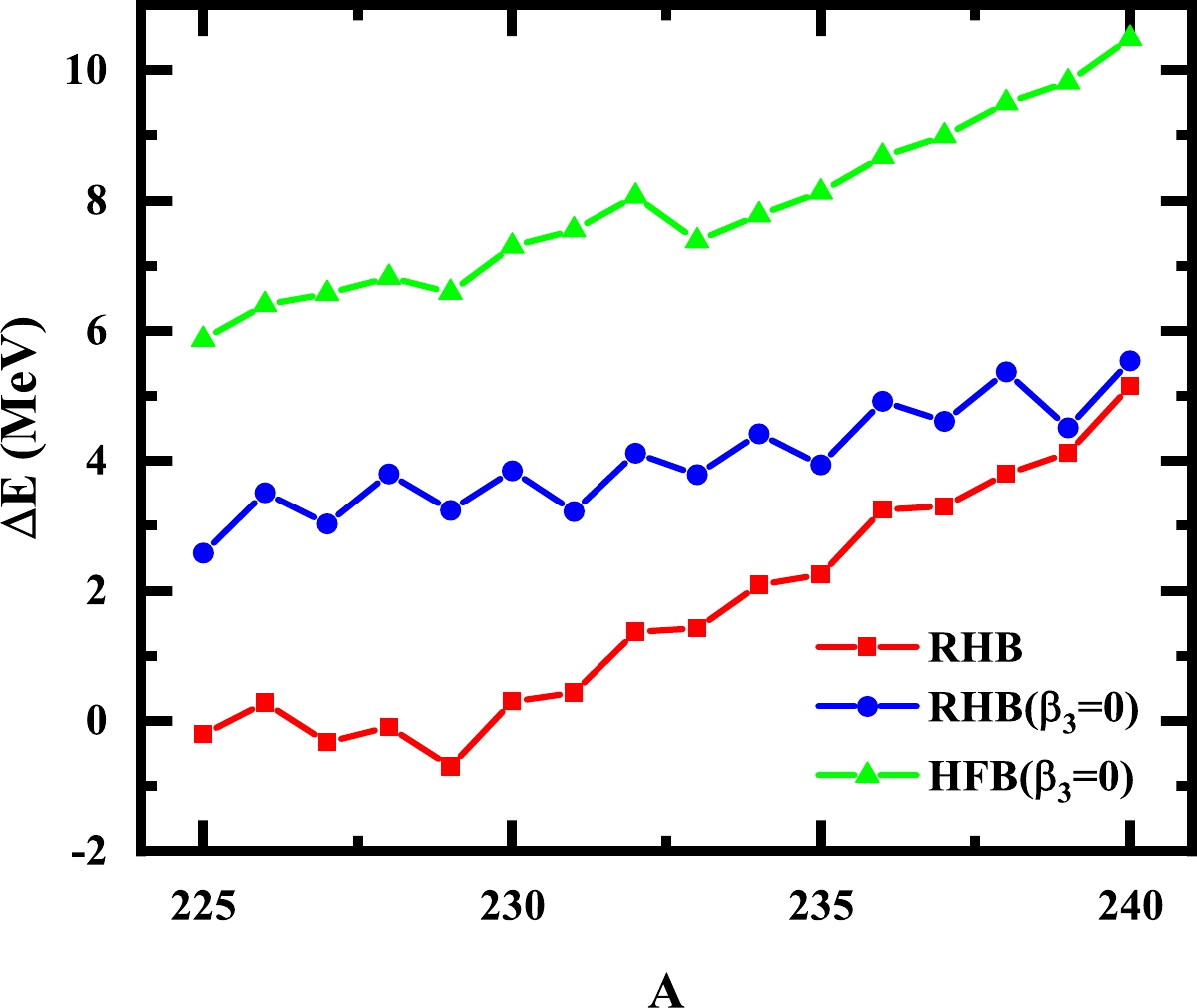
$ ^{225} $ U to$ ^{240} $ U with RHB calculations by considering the lowest points of Figs. 1−4. In Fig. 5, we show a comparison of the ground state binding energies of the RHB calculation with the experimental data [49, 50] and the HFB calculation with Gogny D1S [51]. The red curve is the result of the RHB calculation including the octupole deformation, the blue curve is the result of the RHB calculation considering only the symmetric cases, the green curve is the result of the non-relativistic Hartree-Fock-Bogoliubov calculation, and the black curve represents the experimental values.
Figure 5. (color online) Comparison of ground state binding energies of U-isotopes. A represents the mass number of uranium. The red curve is the result of the RHB calculation including the octupole deformation, the blue curve is the result of the RHB calculation considering only the symmetric cases, the green curve is the result of the non-relativistic Hartree-Fock-Bogoliubov calculation, and the black curve represents the experimental values.
In Fig. 6, we show the difference between the theoretically calculated binding energies and experimental data. The root mean square (RMS) deviations for the binding energy given by the RHB calculations, including the reflection asymmetric deformation, are 2.42 MeV for all the U isotopes. Without the reflection-asymmetric deformation, the total RMS deviation is 4.12 MeV; in the HFB results, the total RMS deviation is 7.98 MeV. These results indicate that for both even-even and odd-A isotopes, the description of the nuclear masses is significantly improved by including the reflection-asymmetric deformation effect.
-
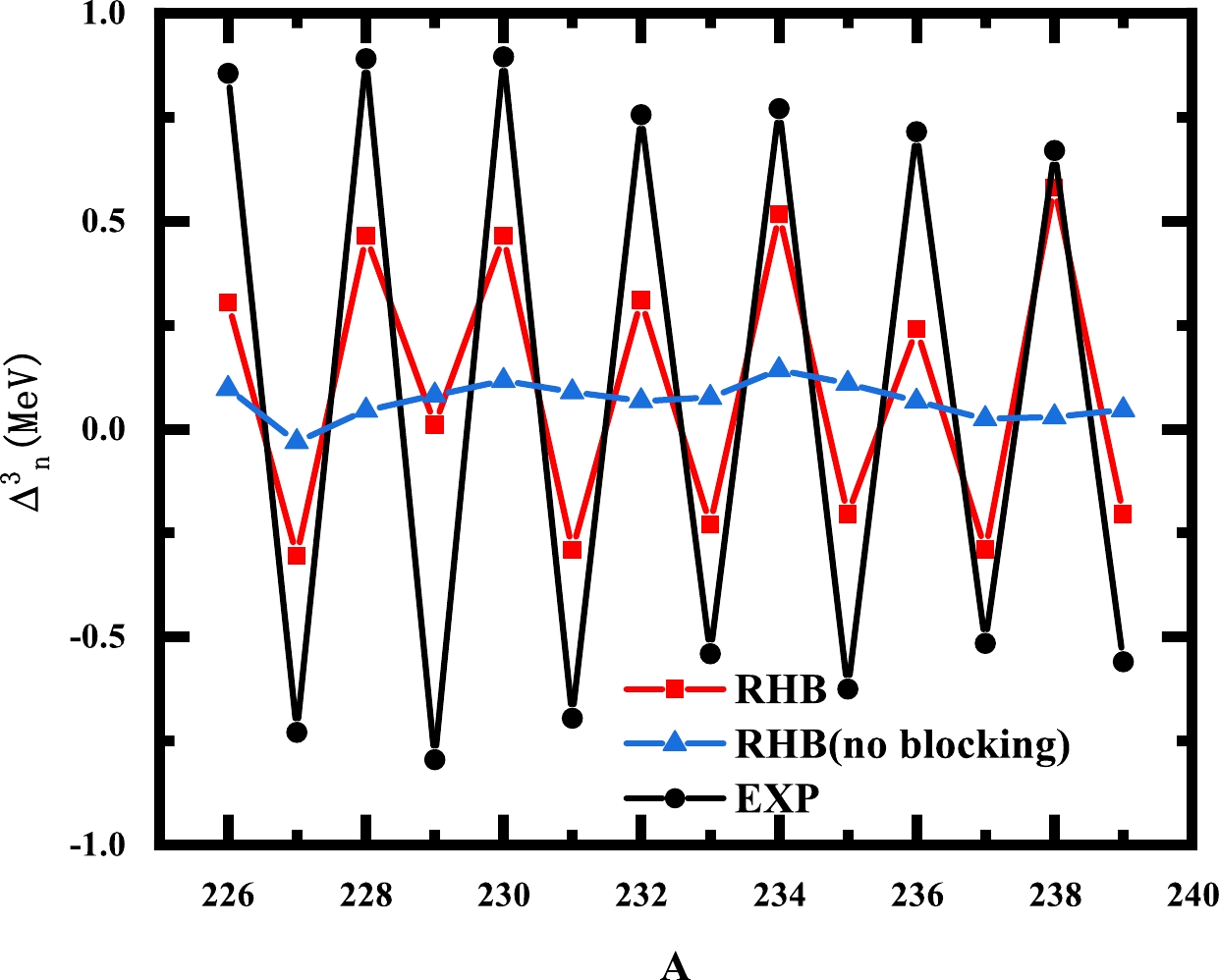
The three-point pairing energy, which is often used to quantify the odd-even staggering (OES) of binding energies, can also be used to access the strength of pairing correlations [52].
$ \Delta_n^3(N)=\frac{1}{2}[B(N-1)-2B(N)+B(N+1)], $

(18) where
$ B(N) $ is the binding energy of a nucleus with N particles. In Eq. (20), since we calculate the U-isotopes, the proton number is fixed, and N denotes the neutron number.In Fig. 7, we show the three-point pairing energy of U-isotopes obtained in the automatic blocking and no blocking RHB calculations. In general, we reproduce the experimental data, and our calculated values are slightly smaller than the experimental data. However, when compared to the results without blocking, the calculations incorporating blocking can clearly demonstrate the distinction between odd and even nuclei. We tried to change the strength of pairing interaction to decrease the deviations between the three-point pairing energies of RHB calculations and experimental data. However, as we know, the deformation of superheavy nuclei is very sensitive to pairing interaction, and when we change the strength of the pairing interaction, the deformation of the ground state will slightly change. To find the real ground state of the U isotopes, we need to calculate the PESs of each nuclei. Thus, it is very difficult to include a discussion on the strength of the pairing interaction in this paper. We hope to present this discussion in the near future.
-
In this work, we applied the RHB method with density-dependent meson exchange parameter (DD-ME2) and separable pairing interaction to calculate the ground state properties of U isotopes from
$ ^{225} $ U to$ ^{240} $ U.To calculate the odd A nuclei, we introduced an automatic blocking method into the RHB calculation. By blocking the lowest quasiparticle orbital in each iteration, we saved a significant amount of computational time to obtain the PES of the odd-A nuclei in relation to that required when blocking the orbitals individually.
We obtained the PES of both even and odd-A nuclei of the U isotopes in the
$ (\beta_2, \beta_3) $ plane from RHB calculations. By searching for the minimum binding energy in the PES of our calculation, we obtained the ground state of the U-isotope. Moreover, we found that for most of the U isotopes, ground states with octupole deformation are preferred. In addition, we compared the binding energy and three-point pairing energy with the experimental data. Our results are much closer to the experimental data than the RHB and HFB calculations without reflection asymmetry deformation.In the future, we will investigate the ground state properties of the actinide nuclei with more types of relativistic mean field parameters such as NL3 [53], DD-PC1 [27], and PC-PK1 [30]. In addition, we will discuss the effect of the strength of the pairing interaction on the ground state properties, especially the pairing energy.
-
We would like to thank Prof. Peter Ring (TMU) for the friendly discussions and Prof. Yifei Niu (LZU) for the great advice.
A study of U-isotope ground state properties with covariant energy density functional
- Received Date: 2024-01-19
- Available Online: 2024-06-15
Abstract: In this study, we systematically analyzed the ground state of uranium isotopes from 225 to 240. In our calculations, we used the covariant energy density functional of density-dependent meson exchange interaction (DD-ME2) with separable pairing interaction (TMR). Using the multiple deformation constraint, we calculated the potential energy surface (PES) of the uranium isotopes for both even-even and even-odd nuclei with quadrupole and octupole deformation. Based on our calculation and upon comparing the experimental data and Hartree-Fock-Bogoliubov calculations with Gogny D1S calculation data, the ground state of uranium isotopes with reflection-asymmetric deformation was found to be preferred.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: