J/ψ pair hadroproduction at next-to-leading order in nonrelativistic-QCD at ATLAS

Currently, nonrelativistic QCD (NRQCD) [1] is the standard tool in the study of heavy quarkonium physics. In this framework, a quarkonium production process can be factorized into two parts: short-distance coefficients (SDCs) and long-distance NRQCD matrix elements (LDMEs). The SDCs can be calculated by perturbative theory, whereas the LDMEs are strongly ordered by the relative velocity v between the quark and anti-quark inside the quarkonium. NRQCD has been applied in single quarkonium production and tested by various experiments [2−13].

Besides single quarkonium production, multi-quarkonuim production provides another ideal laboratory to understand the quarkonium production mechanism. At the LHC, the LHCb Collaboration first measured the $ J/\psi $ pair production at the center-of-mass energy $ \sqrt{s}=7\; \mathrm{TeV} $ with an integrated luminosity of $ 35.2\; \mathrm{pb}^{-1} $ in 2011 [14]. Then, in 2013, the CMS Collaboration further released the data of $ J/\psi $ pair production [15] with a much larger transverse moment range, providing a good platform for testing the validity of NRQCD in quarkonium pair production. Besides, the ATLAS Collaboration also released the data of the $ J/\psi $ pair production [16], with a large transverse momentum cut imposed on both $ J/\psi $.

Regarding the theory describing $ J/\psi $ pair production, Refs. [17−19] reported the leading order (LO) calculation of the $ J/\psi $ pair production in the color singlet model (CSM). The relativistic correction to the $ J/\psi $ pair production was reported in Ref. [20]. This correction can significantly dilute the discrepancy between LO results and experimental data. Furthermore, a partial next-to-leading order ($ \mathrm{NLO}^{\star} $) correction for $ J/\psi $ pair production was presented by Lansberg and Shao [21, 22]. They concluded that the $ \mathrm{NLO}^{\star} $ yield can approach the full NLO result at large $ p_T $, which is the transverse momentum of one of the two $ J/\psi $; thus, the $ \mathrm{NLO}^{\star} $ results constitute a more precise theoretical prediction in this region. The full NLO predictions for color singlet (CS) channel were reported in a previous work of ours [23]. In addition, Kniehl and He provided complete LO predictions within the NRQCD framework by including all possible S-wave and P-wave color singlets and color octet Fock states [24]. All the works mentioned above performed calculations based on the single parton scattering (SPS) mechanism. The contribution of double parton scattering (DPS) was evaluated in Refs. [22, 25−27]; this contribution is expected to be significant. Given that the predictions for DPS are highly model-dependent, it is necessary to accurately calculate the NLO for the SPS contribution before one can extract the DPS contribution.

Based on the above discussion, to further study the multi-quarkonium production process, it is necessary to evaluate the $ J/\psi $ pair production to NLO for more channels, encompassing $ {}^{1}S_0^{[8]} $, $ {}^{3}S_1^{[8]} $, and $ {}^{3}P_J^{[8]} $. Because $ {}^{1}S_0^{[8]} $ was found to contribute the most to single $ J/\psi $ production [28], in this study we focused on the $ {}^{1}S_0^{[8]} $ channel and evaluated each $ J/\psi $ in $ {}^{3}S_1^{[1]} $ and $ {}^{1}S_0^{[8]} $ fock states at the NLO level. The calculations of $ {}^{3}S_1^{[8]} $ and $ {}^{3}P_J^{[8]} $ channels will be analyzed in future studies. The NLO result reduces theoretic uncertainties and opens new kinematic enhanced topologies, which dominate at large $ p_T $. For example, the differential cross section ${\rm d}\sigma/{\rm d}p_T^2$ at large $ p_T $ behaves as $ p_T^{-8} $ at LO, while it behaves as $ p_T^{-6} $ at NLO owing to double parton fragmentation contributions [29].

In NRQCD, the cross section of $ J/\psi $ pair production at the LHC can be factorized as [1]

where $ f_{i/p}(x_{1,2}) $ represents the parton distribution functions (PDFs), $ x_1 $ and $ x_2 $ are the momentum fraction of initial state partons from the protons, and $ d\hat{\sigma} $ are partonic short-distance coefficients. In this study, we set either $ n_1=n_2={}^{3}S_1^{[1]} $ or $ n_1=n_2={}^{1}S_0^{[8]} $ in Eq. (1).

In the LO calculation, there are two subprocesses: $ g+g{\rightarrow }J/\psi+J/\psi $ and $ q+\bar{q}{\rightarrow }J/\psi+J/\psi $; only the former is considered because the contribution of the other process is highly suppressed by the quark PDFs. In the NLO case, both the gluon fusion process and the quark gluon process ($ q+g\rightarrow 2J/\psi+q $) are taken into account because they jointly constitute a non-negligible contribution. Typical Feynman diagrams at LO and NLO are shown in Fig. 1.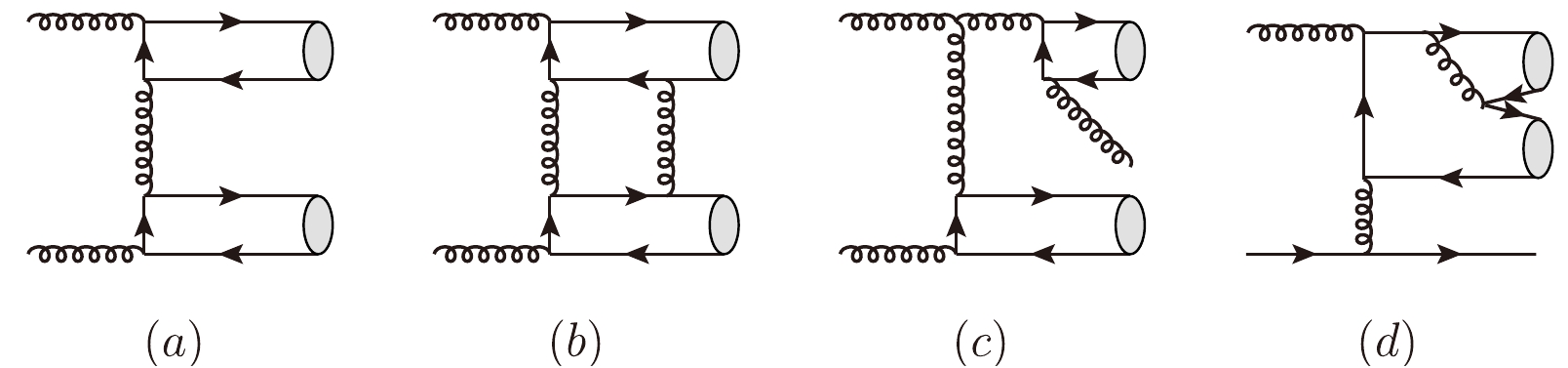

Figure 1.  Typical Feynman diagrams for $ J/\psi $ pair production in $ {}^{3}S_1^{[1]} $ and $ {}^{1}S_0^{[8]} $ channels, including LO and NLO.

The NLO contributions can be divided into two parts: virtual and real corrections. The virtual correction that arises from loop diagrams only includes the gluon fusion process, which is also the case of the LO contribution, while for the real correction, in addition to the gluon fusion process, the process $ q+g\rightarrow 2J/\psi+q $ should also be taken into account.

In the virtual correction, the ultraviolet (UV) and infrared (IR) divergences usually exist. We use the dimensional regularization scheme to regularize the UV and IR divergences. The Coulomb divergence caused by the virtual gluon line connecting the quark pair in a $ J/\psi $ is regularized by the relative velocity v. The UV divergences can be renormalized by counterterms. The renormalization constants include $ Z_{2} $, $ Z_{3} $, $ Z_{m} $, and $ Z_{g} $, corresponding to the quark field, gluon field, quark mass, and strong coupling constant $ \alpha_{s} $, respectively. In our calculations, $ Z_{g} $ is defined in the modified-minimal-subtraction ($ \mathrm{\overline{MS}} $) scheme, while for the other three, the on-shell ($ \mathrm{OS} $) scheme is adopted, which reads

where $ \beta _{0}=\dfrac{11}{3}C_{A}-\dfrac{4}{3}T_{F}n_{f} $ is the one-loop coefficient of the QCD beta function; $ n_{f}=4 $ is the number of active quarks in our calculation; $ \beta _{0}^{'}=\dfrac{11}{3}C_{A}-\dfrac{4}{3}T_{F}n_{lf} $ with $ n_{lf}=3 $ is the number of light quarks; $ C_{A}=3 $ and $ T_{F}=1/2 $ are attributed to the SU(3) group; and $ \mu_r $ is the renormalization scale.

As mentioned above, there are two processes involved in the real corrections: $ g+g\rightarrow J/\psi+J/\psi+g $ and $ q+g\rightarrow J/\psi+J/\psi+q $. It is known that IR divergence exists in these processes because of the phase space integration, which can be canceled by the IR singularities left in the virtual correction. According to the different regions of the phase space, the IR divergence can be categorized as soft or collinear. In this study, we used the two-cutoff phase space slicing method [30] to isolate the two types of IR singularities; thus, the cross section of the real correction can be expressed as

where $\rm HC$ and $\rm \overline{HC}$ represent hard collinear and hard noncollinear contributions, respectively.

Now, the cross sections for the $ J/\psi $ pair production at NLO can be expressed as

The soft and collinear divergences from real corrections cancel divergences from virtual corrections. Thus, the final NLO contributions are IR safe.

Because there are two $ J/\psi $ states in the final state, the LO contributions behave as $ p_T^{-8} $ when $ p_T $is large. However, at the NLO level, there are contributions that lead to $ p_T^{-6} $ behavior [29] [Fig. 1 (c) and (d)]. Therefore, we expect that the NLO contribution dominates at large $ p_T $, especially for the CMS and ATLAS data, where a relatively large lower $ p_T $ cutoff exists [15, 16]. This expectation is confirmed by the numerical results presented below.

The $ J/\psi $ pair production process is complicated. Thus, in our calculations, the package FEYNARTS [31] was used to generate the Feynman diagrams and amplitudes. The phase space integration was evaluated by employing the package Vegas [32].

For numerical calculations, the CTEQ6L1 and CTEQ6M parton distribution functions [33, 34] were used. The renormalization scale $ \mu_r $ and factorization scale $ \mu_f $ were set as $ \mu_r=\mu_f=m_T $, with $ m_T=\sqrt{p_T^2+16m_c^2} $ and charm quark mass $ m_c=M_{J/\psi}/2=1.55\; \mathrm{GeV} $. In the two-cutoff method, the soft and collinear cutoffs, $ \delta_s $ and $ \delta_c $, were set as $ \delta_s=10^{-2} $ and $ \delta_c=10^{-4} $. Theoretical uncertainties were estimated by varying $ \mu_r=\mu_f $ from $ m_T/2 $ to $ 2m_T $.

The CS LDME $\langle\mathcal{O}(^3 S_1^{[1]})\rangle^{J/\psi}=1.16 ~\rm{GeV}^3$ was calculated by using the ${B-T}$ potential model [35]. Concerning CO LDME $\langle\mathcal{O}(^1 S_0^{[8]})\rangle^{J/\psi}=0.089 ~\rm{GeV}^3$, it was taken from [36]; this value was obtained by fitting experimental data.

In this section, we report our results for the $ J/\psi $ pair production. The ATLAS conditions are [16]:

We also consider the contributions of the feeddown processes $ p+p\rightarrow J/\psi+\psi(2S)+X\rightarrow 2J/\psi+X $ and $p+p\rightarrow J/\psi+\chi_{cJ}+X\rightarrow 2J/\psi+X$, which are estimated to be $30$% of the direct production [19].

First, we compare our prediction for the distribution of the transverse momentum $ p_{T J/\psi J/\psi} $ of the $ J/\psi $ pair with the ATLAS data, as shown in Fig. 2. In this case, only the NLO contribution exists, because at LO, $ p_{T J/\psi J/\psi} $ is always zero. Note that the behavior of the NRQCD result is consistent with the experimental data, except for the first four bins. Therefore, in the NRQCD framework, the NLO calculation can describe the ATLAS data in the region $ p_{T J/\psi J/\psi}> $ 10 GeV. We can see that the $ {}^{1}S_0^{[8]} $ channel contributes little in this region; it only contributes significantly when $ p_{T J/\psi J/\psi} $ is small.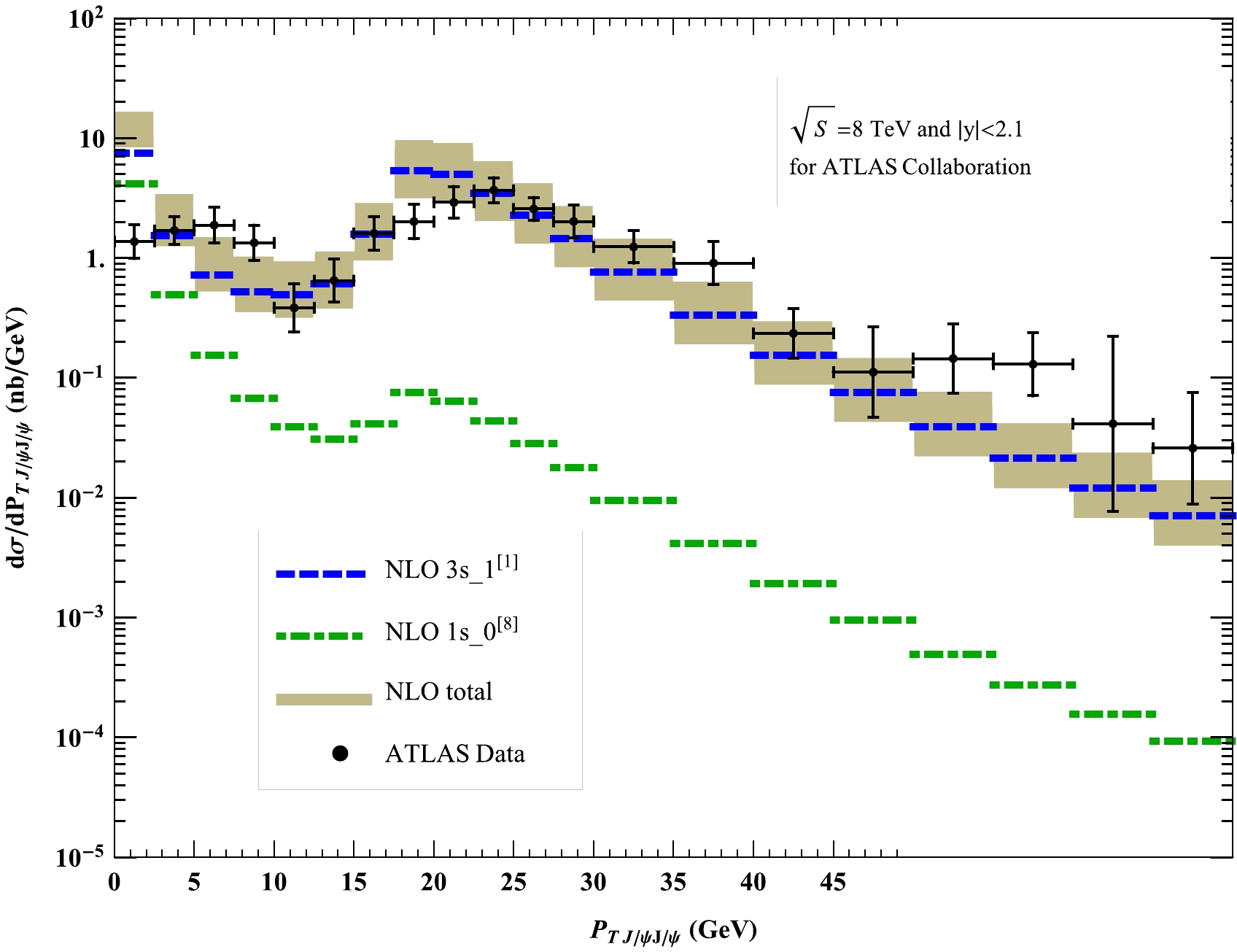

Figure 2.  (color online). Differential cross sections in bins of the transverse momentum of $ J/\psi $ pair at ATLAS. The data are extracted from Ref. [16]. The dashed and dot dashed lines denote the NLO $ {}^{3}S_1^{[1]} $ and $ {}^{1}S_0^{[8]} $ results, respectively, and the band denotes the NLO total result, where the uncertainties are due to scale choices, as mentioned in the text.

The invariant mass distribution at ATLAS is shown in Fig. 3. Again, the $ {}^{1}S_0^{[8]} $ channel exhibits large contributions in the medium and large $ M_{J/\psi J/\psi} $ regions. The summation of the $ {}^{3}S_1^{[1]} $ and $ {}^{1}S_0^{[8]} $ channels indicates that the NLO result can well describe the first three bins of the ATLAS data. For other bins, because the ATLAS data are not smooth, there is large uncertainty. Our NLO prediction can describe the data to a certain extent thanks to the $ {}^{1}S_0^{[8]} $ contribution.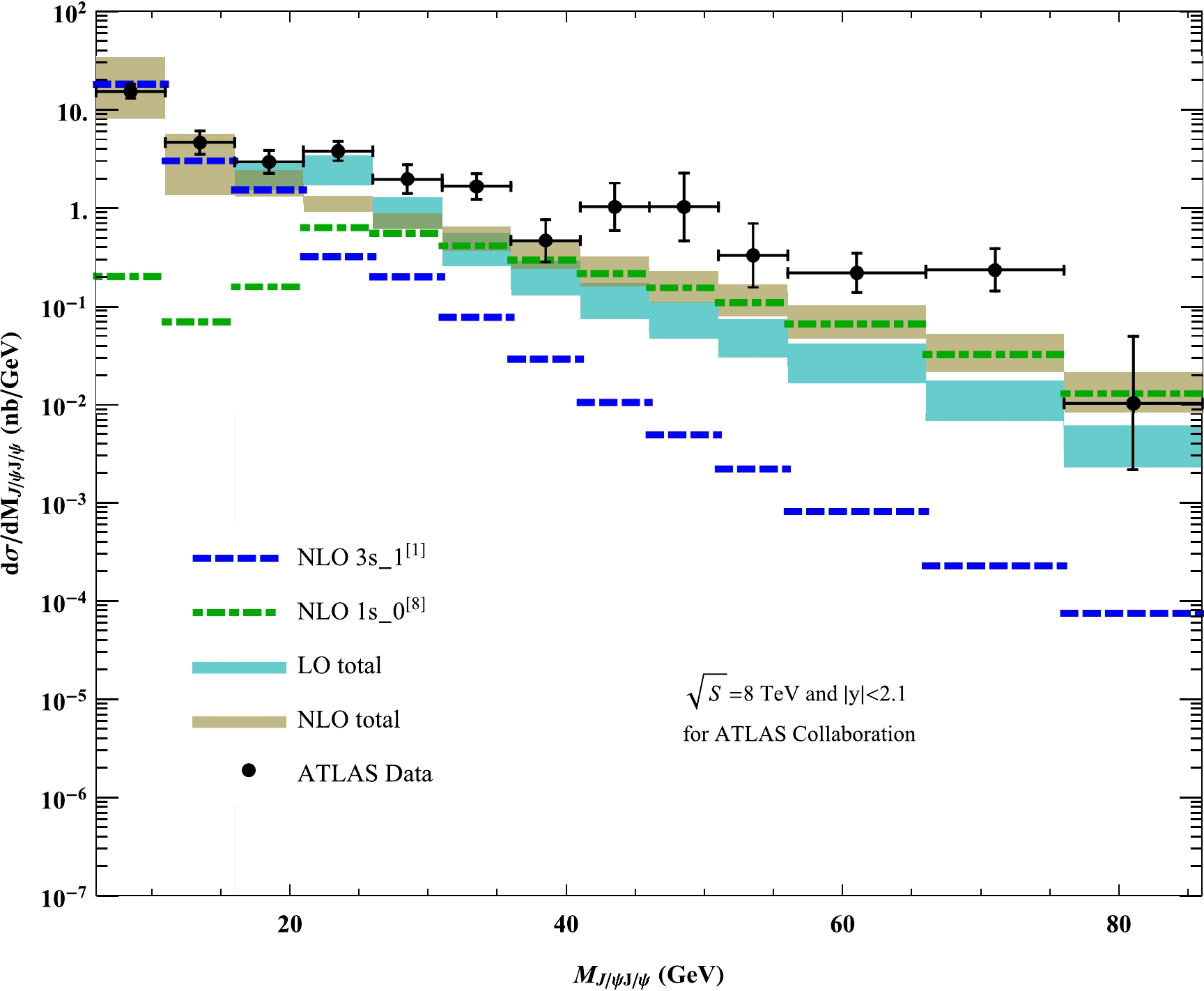

Figure 3.  (color online). Differential cross sections in bins of the $ J/\psi $ pair invariant mass at ATLAS. The data are extracted from Ref. [16]. The dashed and dot dashed lines denote the NLO $ {}^{3}S_1^{[1]} $and LO $ {}^{1}S_0^{[8]} $ results, respectively, and the two bands denote the LO and NLO total results, where the uncertainties are due to scale choices, as mentioned in the text.

The distribution of the $ J/\psi $ pair rapidity difference $ |\Delta y| $ at ATLAS is shown in Fig. 4. The $ {}^{1}S_0^{[8]} $ channel exhibits a large contribution in the medium and large $ |\Delta y| $ regions and dominates at large$ |\Delta y| $. The conclusion is the same as that for the $ J/\psi $ pair invariant mass distribution: the NLO result can approximately describe the data to a certain extent.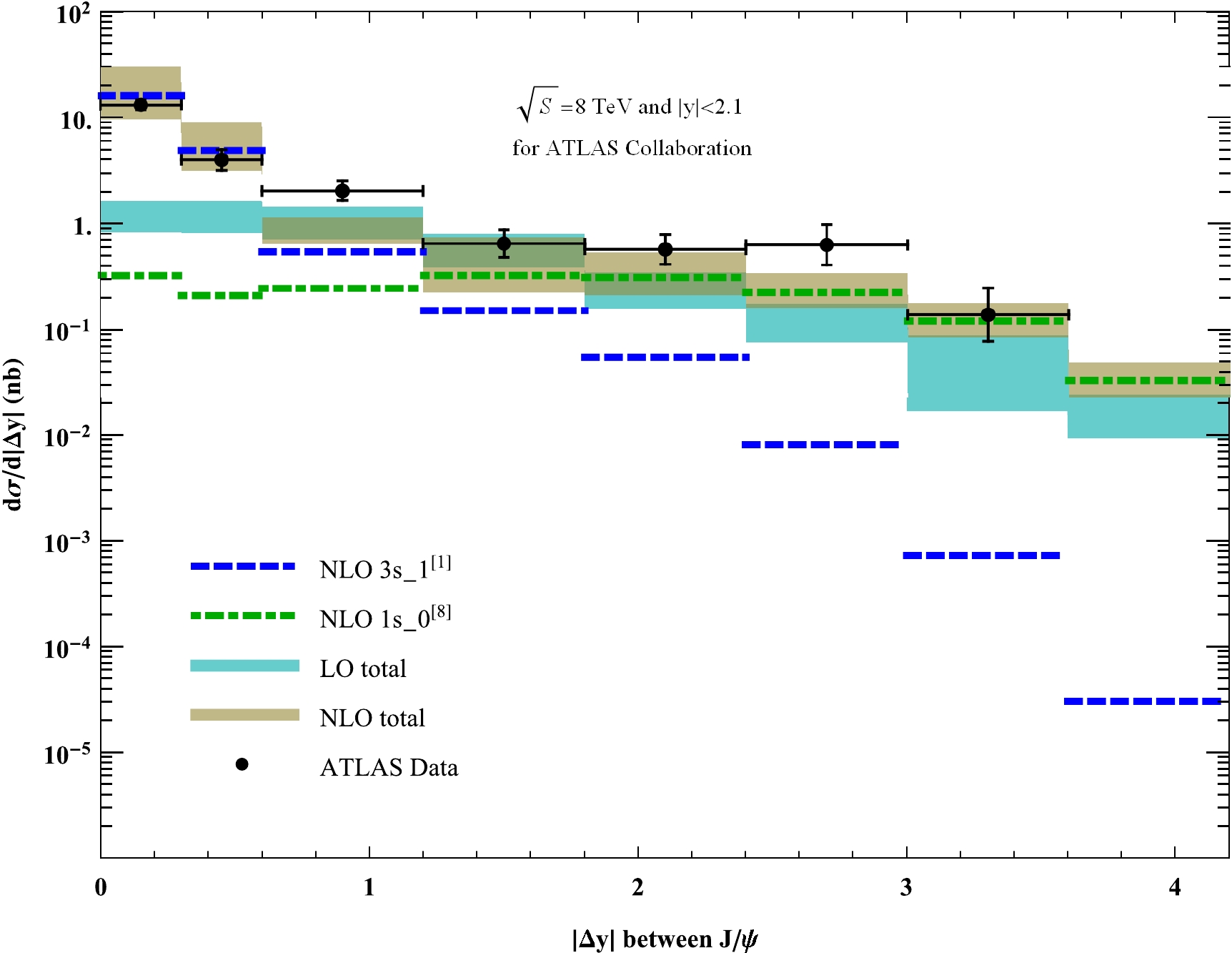

Figure 4.  (color online). Differential cross sections in bins of the $ J/\psi $ pair $ |\Delta y| $at ATLAS. The data are extracted from Ref. [16]. The dashed and dot dashed lines denote the NLO $ {}^{3}S_1^{[1]} $ and NLO $ {}^{1}S_0^{[8]} $ results, respectively, and the two bands denote the LO and NLO total results, where the uncertainties are due to scale choices, as mentioned in the text.

The ATLAS and CMS cases can be compared. The latter was addresed in a previous study of ours, $ J/\psi $ Pair Hadroproduction at Next-to-Leading Order in Nonrelativistic-QCD at CMS [37], where we concluded that the NRQCD predictions cannot describe the experimental data at all; the same conclusion was drawn by Lansberg and Shao [22]. However, in this study, we conclude that the NRQCD can describe the experimental data to a certain extent. The reason for NRQCD to fail in explaining the CMS data may lie in the experimental cut:

This cut is abnormal compared to that of ATLAS. In particular, in line two of the cut, the range of the rapidity is dynamical. We do not know whether NRQCD works well with such a cut. We hypothesize that the large discrepancies are caused by the strange cut. We hope new experimental data can be released with a normal cut in the future. Thus, we will be able to re-calculate this process and draw a clear conclusion.

In the framework of NRQCD factorization, we performed full NLO $ J/\psi $ pair production, including the $ {}^{3}S_1^{[1]} $ and $ {}^{1}S_0^{[8]} $ channels. We found that NLO corrections are essential for $ J/\psi $ pair production at ATLAS, compared to the LO results.

For ATLAS, our calculations can describe the data to a certain extent, but a definite conclusion cannot be drawn because the data have large uncertainties. Therefore, more data are crucial for further study of the double-$ J/\psi $ production. In the future, we will add the ignored $ {}^{3}S_1^{[8]} $ and $ {}^{3}P_J^{[8]} $ channels. Thus, we will achieve a higher precision in prediction with the contribution of SPS. In this way, contributions from other mechanisms, such as DPS, will be clarified.

We thank Y. Q. Ma, C. Meng and K. T. Chao for valuable discussions and suggestions.