-
In the 1960s, Zel'dovich and Goldansky predicted the possibility of two-proton (
$ 2p $ ) radioactivity from the ground state of a nucleus near or beyond the proton drip-line [1−3]. Goldansky pointed out that the predicted$ 2p $ radioactivity half-life was greater than$ 10^{-12} $ s, and its decay energy was lower than that of the corresponding one-proton ($ 1p $ ) radioactivity. This type of$ 2p $ radioactivity was called true$ 2p $ radioactivity [4]. Because of the pairing effect, true$ 2p $ radioactivity usually occurs in even-Z nuclei so that the corresponding$ 1p $ decay channel is forbidden. Accordingly, true$ 2p $ decay energies may have the following features:$ Q_{2p}>0 $ and$ Q_{p}<0 $ , where$ Q_{2p} $ and$ Q_{p} $ are the$ 2p $ and$ 1p $ decay energies, respectively. However, true$ 2p $ radioactivity was not observed until 2002 because the production of nuclei near the drip-line is difficult. In 2002, true$ 2p $ radioactivity was discovered from$ ^{45} $ Fe at the fragment separator of GSI and at the SISSI-LISE3 facility of GANIL [5, 6]; the measured half-lives of the$ 2p $ radioactivity were 4.7$ _{-1.4}^{+3.4} $ ms and 3.2$ _{-1.0}^{+2.6} $ ms, respectively. Several years later, more nuclei with true$ 2p $ radioactivity were synthesized:$ ^{48} $ Ni [7],$ ^{54} $ Zn [8], and$ ^{67} $ Kr [9]. Meanwhile, the measured$ 2p $ decay half-lives of$ ^{48} $ Ni,$ ^{54} $ Zn, and$ ^{67} $ Kr were at the level of ms. To date,$ 2p $ radioactivity with long half-lives has only been observed from the above four nuclei. However,$ 2p $ radioactivity from the very short-lived nuclear ground states of$ ^{6} $ Be [10],$ ^{12} $ O [11, 12],$ ^{16} $ Ne [11, 13],$ ^{19} $ Mg [14], and$ ^{30} $ Ar [15] has been observed. The orders of magnitude of the measured$ 2p $ decay half-lives were approximately at the level of ps.Since the prediction of
$ 2p $ radioactivity, many models have been proposed to describe its decay properties [16−45]. Generally, the$ 2p $ radioactivity process can be described by the following three pictures: (i) Diproton ("$ ^{2} $ He") emission. A strongly correlated emission of the two protons which, owing to the proton–proton attraction, form an$ ^{1}S_{0} $ resonance. Because the proton–proton system is not bound, this diproton structure most likely decays under the Coulomb barrier and two individual protons are observed outside the nucleus [16−32]; (ii) “Three-body decay.” Completely uncorrelated emission, where only energy, momentum, and angular momentum conservation have to be respected for simultaneous emission [30−45].However, the mechanism of
$ 2p $ radioactivity is not yet clear. It is necessary to study the structure of extremely proton-rich nuclei because$ 2p $ radioactivity is strongly dependent on the nuclear structure. Although proton-rich nuclear structures have been investigated using various models [46−55], most studies are not directly correlated with the mechanism of$ 2p $ radioactivity.Recently, Saxena et al. studied the
$ 2p $ radioactivity of light mass nuclei (A = 18−34) with a$ 2p $ halo using the relativistic mean-field plus BCS approach and the macroscopic-microscopic model with the Nillson Strutinsky prescription [56]. It was shown that a$ 2p $ halo-like structure is more likely to decay via direct diproton emission. Generally, the formation of a halo can be understood as the scattering of particle pairs into the continuum containing low-lying resonances with small angular momenta by the pairing correlation [57−62]. Therefore, the$ 2p $ radioactivity of the nuclei with a$ 2p $ halo may not only be correlated with the single-particle resonant states in the continuum but also be relevant to the pairing correlation.However, in the work of Saxena et al., the tensor force was neglected. Tensor force is the noncentral and nonlocal spin-spin interaction and serves as an important component of the nucleon-nucleon (NN) interaction. It has been introduced into various nuclear models, such as the shell model [63], ab initio approach [64], and self-consistent mean-field theory [65−67]. The single-particle state evolutions of exotic nuclei are described successfully when the tensor force is included [63−80]. In our previous study, we found that the giant neutron halo of neutron-rich Ca isotopes is suppressed owing to the shift in single-particle resonant orbits in the continuum caused by the tensor force [81]. This drives us to consider whether the low-lying continuum of
$ 2p $ halo nuclei is influenced by the tensor force and whether$ 2p $ radioactivity is further affected. This constitutes the first motivation of this study.On the other hand, relevant studies have suggested that the halo is strongly influenced by the pairing correlation [59, 82−84]. The large pairing effect on weakly bound neutrons, leading to the pairing anti-halo effect, has been discussed [82]. The influence of pairing interactions on the asymptotic properties of nucleonic distributions has demonstrated that the size of the neutron halo dramatically depends on the behavior of the pairing interaction at low density [83]. However, during a
$ 2p $ decay process, little is known about the correlation between the two emitted protons. Therefore, it is interesting to study the pairing correlation effect on the$ 2p $ radioactivity of nuclei with a$ 2p $ halo. This is the second motivation of this study.It is well known that Skyrme-Hartree-Fock-Bogoliubov (SHFB) theory is a powerful tool to describe exotic nuclei [85−88]. It can provide a unified and self-consistent description of both the mean-field and pairing field in terms of Bogoliubov quasi-particles. Based on the above two motivations and the advantage of SHFB theory, we investigate the tensor force and pairing correlation effects on the
$ 2p $ radioactivity of$ 2p $ halo nuclei in the framework of spherical SHFB theory [85−88]. This article is organized as follows. In Sec. II, the theoretical framework is presented, Sec. III presents the calculated results and discussions, and several conclusions are drawn in the final section. -
The fundamental task of nuclear many-body physics is to understand the nuclear structure and reaction using many-body calculations starting from the NN interaction. Usually, the modern NN interaction refers to the bare nuclear force (for instance, Argonne v18(95) [89] and Reid(93) [90]), meson exchange potential [91−95], and potential from low-energy quantum chromodynamics via chiral effective field theory [96, 97]. Nevertheless, the phenomenological NN interaction still plays an important role in nuclear many-body calculations. The Skyrme interaction is a kind of phenomenological NN interactions. Many properties of unstable nuclei are described successfully within SHFB theory, including tensor force [85−88]. In this section, spherical SHFB theory with the tensor force and the specific investigation procedure of this study are introduced.
-
The Skyrme interaction is written as
$ \begin{array}{*{20}{l}} V_{\rm Skyrme}=V_{12}+V_{12}^{T}, \end{array} $

(1) where
$ V_{12} $ and$ V_{12}^{T} $ denote the usual and tensor force parts of the interaction, respectively.The expression for
$ V_{12} $ is [86]$ \begin{aligned}[b] V_{12} =&t_{0}(1+x_{0}\mathbf{P}_{\sigma })\delta (\mathbf{r}_{1}-\mathbf{r} _{2}) \\ &+\frac{1}{2}t_{1}(1+x_{1}\mathbf{P}_{\sigma })\left[ \mathbf{k}^{{\prime }2}\delta (\mathbf{r}_{1}-\mathbf{r}_{2})+\delta (\mathbf{r}_{1}-\mathbf{r} _{2})\mathbf{k}^{2}\right] \\ &+t_{2}(1+x_{2}\mathbf{P}_{\sigma })\mathbf{k}^{{\prime }}\cdot \delta ( \mathbf{r}_{1}-\mathbf{r}_{2})\mathbf{k}\\ &+\frac{1}{6}t_{3}(1+x_{3}\mathbf{P}_{\sigma })\rho ^{\gamma }\delta ( \mathbf{r}_{1}-\mathbf{r}_{2}) \\ &+ {\rm i} W_{0}(\mathbf{\sigma }_{1}+\mathbf{\sigma }_{2})\cdot \left[ \mathbf{k} ^{{\prime }}\times \delta (\mathbf{r}_{1}-\mathbf{r}_{2})\mathbf{k}\right] ,\end{aligned} $

(2) where
$ t_{i} $ ,$ x_{i} $ (i =1, 2, 3), and$ W_{0} $ are the parameters of the interaction,$ P_{\sigma } $ is the spin-exchange operator, and$ \sigma _{i} $ are the Pauli matrices. The operator$ \mathbf{k=(\nabla }_{1}-\mathbf{\nabla }_{2})/2i $ acts on the right and$\mathbf{k}^{{\prime }}\mathbf{=-(\nabla }_{1}-\mathbf{\nabla }_{2})/2i$ acts on the left.$ V_{12}^{T} $ can be expressed as [67−79]$ \begin{aligned}[b] V_{12}^{T} =&\frac{T}{2}\left[ (\sigma _{1}\cdot \mathbf{k}^{{\prime }})(\sigma _{2}\cdot \mathbf{k}^{{\prime }})-\frac{1}{3}(\sigma _{1}\cdot \sigma _{2})\mathbf{k}^{{\prime }2}\right] \delta (\mathbf{r}_{1}-\mathbf{r} _{2}) \\ &+\frac{T}{2}\delta (\mathbf{r}_{1}-\mathbf{r}_{2})\left[ (\sigma _{1}\cdot \mathbf{k})(\sigma _{2}\cdot \mathbf{k})-\frac{1}{3}(\sigma _{1}\cdot \sigma _{2})\mathbf{k}^{2}\right] \\ &+\frac{U}{2}\Big[ (\sigma _{1}\cdot \mathbf{k}^{{\prime }})\delta ( \mathbf{r}_{1}-\mathbf{r}_{2})(\sigma _{2}\cdot \mathbf{k})+(\sigma _{2}\cdot \mathbf{k}^{{\prime }})\delta (\mathbf{r}_{1}-\mathbf{r} _{2})\\&\times(\sigma _{1}\cdot \mathbf{k})\Big] -\frac{1}{3}U(\sigma _{1}\cdot \sigma _{2})\mathbf{k}^{{\prime }}\cdot \delta (\mathbf{r}_{1}-\mathbf{r}_{2})\mathbf{k}, \end{aligned} $

(3) where T and U are the strengths of the triplet-even and triple-odd tensor interactions, respectively.
In the pairing channel, a density-dependent δ interaction is employed, whose form is
$ V_{\rm pair}(\mathbf{r}_{1},\mathbf{r}_{2})=V_{0}\left(1-\eta \frac{\rho (\mathbf{r)} }{\rho _{0}}\right)\delta (\mathbf{r}_{1}-\mathbf{r}_{2}), $

(4) where
$ V_{0} $ denotes the pairing strength. It is determined along with a certain cutoff quasiparticle energy using the mean neutron pairing energy gap of$ ^{120} $ Sn (1.31 MeV). Usually, the cutoff quasiparticle energy is taken as 60 MeV. In Eq. (4),$ \rho (\mathbf{\pmb r}) $ is the isoscalar local density, and$ \rho _{0} $ is the nuclear matter saturation density, fixed at 0.16 fm$ ^{-3} $ . The η values are$ 0 $ ,$ 0.5 $ , and$ 1 $ for volume, mixed, and surface pairing, respectively.The total energy E of a nucleus is the sum of the kinetic, usual Skyrme, pairing, Coulomb, and tensor energies,
$ \begin{aligned}[b] E =&K+E_{\rm Skyrme}+E_{\rm Pair}+E_{\rm Coul}+E_{\rm Tensor} \\ =&\int {\rm d}^{3}\mathbf{r}[k(\mathbf{r})+\varepsilon _{\rm Skyrme}(\mathbf{r} )+\varepsilon _{\rm Pair}(\mathbf{r})\\&+\varepsilon _{\rm Coul}(\mathbf{r})+\varepsilon _{\rm Tensor}(\mathbf{r})], \end{aligned} $

(5) where k,
$ \varepsilon _{\rm Skyrme} $ ,$ \varepsilon _{\rm Pair} $ ,$ \varepsilon _{\rm Coul} $ , and$ \varepsilon _{\rm Tensor} $ are the corresponding energy densities. Their expressions can be found in Ref. [86].In the case of spherical symmetry, single-particle wave functions have the good quantum numbers (nljmq), and all the solutions inside an (nljq)-block are degenerate. Furthermore, the radial part of the wave functions can be chosen to be real. Thus, the wave function is
$ \varphi _{i}(E,\mathbf{r}\sigma )=\frac{u_{i}(nlj,r)}{r}Y_{ml}^{(l)}(\bar{r})\langle lm_{l}\frac{1}{2}\sigma |jm\rangle ,\;i=1,2, $

(6) $ u_{1} $ and$ u_{2} $ are the radial wave functions.The particle and pairing densities can be written using the radial functions
$ \rho (r)=\frac{1}{4\pi r^{2}}\mathop \sum \limits_{nlj} (2j+1)u_{2}^{2}(nlj,r), $

(7) $ \widetilde{\rho }(r)=-\frac{1}{4\pi r^{2}}\mathop \sum \limits_{nlj} (2j+1)u_{1}(nlj,r)u_{2}(nlj,r). $

(8) For the normal and abnormal kinetic densities, we have
$ \begin{aligned}[b] \tau (r)=&\mathop \sum \limits_{nlj}\frac{2j+1}{4\pi r^{2}}\left[ \left( u_{2}^{{\prime }}(nlj,r)-\frac{u_{2}(nlj,r)}{r}\right) ^{2}\right.\\&\left.+\frac{l(l+1)}{ r^{2}}u_{2}^{2}(nlj,r)\right] , \end{aligned} $

(9) $ \begin{aligned}[b] \widetilde{\tau }(r)=&-\mathop \sum \limits_{nlj}\frac{2j+1}{4\pi r^{2}}\left[ \left( u_{1}^{{\prime }}(nlj,r)-\frac{u_{1}(nlj,r)}{r}\right)\right.\\&\times \left( u_{2}^{{\prime }}(nlj,r)-\frac{u_{2}(nlj,r)}{r}\right) \\&\left.+\frac{l(l+1)}{r^{2}} u_{1}(nlj,r)u_{2}(nlj,r)\right] . \end{aligned} $

(10) Here,
$ u_{i} $ '(nlj,r) (i = 1, 2) is the first order derivative with respect to the radial coordinate r.The spin current vector densities are given by
$ J(r)=\frac{1}{4\pi r^{3}}\mathop \sum \limits_{nlj}(2j+1)\left[ j(j+1)-l(l+1) - \frac{3}{4}\right] u_{2}^{2}(nlj,r), $

(11) $ \begin{aligned}[b] \widetilde{J}(r)=&-\frac{1}{4\pi r^{3}}\mathop \sum \limits_{nlj}(2j+1)\Bigg[ j(j+1)-l(l+1)-\frac{3}{4}\Bigg]\\& \times u_{1}(nlj,r)u_{2}(nlj,r). \end{aligned} $

(12) Generally, the tensor term, also known as the
$ \mathcal{J}^{2} $ term, originates from both the zero-range central and tensor forces. By considering these two types of forces,$\varepsilon _{\rm Tensor}$ can be written as$ \varepsilon _{\rm Tensor}(r)=\frac{1}{2}\alpha (J_{q}^{2}+J_{q\prime }^{2})+\beta J_{q}J_{q\prime }, $

(13) where α and β are the like-particle and proton-neutron coupling constants, respectively. The subscript label q denotes neutrons (protons) and
$ q^{\prime} $ represents protons (neutrons).Because the particle number cannot be preserved by the Bogolyubov transformation, two Lagrangian multipliers
$ \lambda _{N} $ and$ \lambda _{Z} $ are introduced to conserve the average neutron and proton numbers. Then, the SHFB equation is obtained using the stationary condition$ \delta \left[E-\langle \lambda _{N}N+ \lambda _{Z}Z\rangle \right] =0 $ .In the particle-hole channel, the spin-orbit coupling field has the following form [76, 77]:
$ \begin{aligned}[b] B_{s.o.}^{q} =&B_{\rho }+B_{C}+B_{T} \\=&\frac{W_{0}}{2r}\left(2\frac{{\rm d}\rho _{q}}{{\rm d}r}+\frac{{\rm d}\rho _{q^{,}}}{{\rm d}r}\right)+\left(\alpha _{C}\frac{J_{q}}{r}+\beta _{C}\frac{J_{q^{,}}}{r}\right)\\ &+\left(\alpha _{T} \frac{J_{q}}{r}+\beta _{T}\frac{J_{q^{,}}}{r}\right), \end{aligned} $

(14) where
$ B_{\rho } $ ,$ B_{C} $ , and$ B_{T} $ are from the contributions of the particle density, central exchange force, and tensor force, respectively.The coupling constants in Eq. (14) are
$\alpha =\alpha _{C}+\alpha _{T}$ and$\beta =\beta _{C}+\beta _{T}$ . Therefore, Eq. (14) can be modified to$ B_{s.o.}^{q} =\frac{W_{0}}{2r}\left(2\frac{{\rm d}\rho _{q}}{{\rm d}r}+\frac{{\rm d}\rho _{q^{,}}}{{\rm d}r}\right)+\alpha\frac{J_{q}}{r}+\beta\frac{J_{q^{,}}}{r}. $

(15) Moreover,
$ \alpha _{C} $ ,$ \beta _{C} $ ,$ \alpha _{T} $ , and$ \beta _{T} $ have the following forms:$ \begin{aligned}[b] \alpha _{C} =&\frac{1}{8}(t_{1}-t_{2})-\frac{1}{8}(t_{1}x_{1}-t_{2}x_{2}), \\ \beta _{C} =&-\frac{1}{8}(t_{1}x_{1}+t_{2}x_{2}), \end{aligned} $

(16) $ \begin{aligned}[b] \alpha _{T} =&\frac{5}{12}U, \\ \beta _{T} =&\frac{5}{24}(T+U). \end{aligned} $

(17) Expressions for the normal effective mass field M
$ _{q} $ , abnormal effective mass field$ \widetilde{\mathit{M}}_{q} $ , and other potential fields (the particle-hole field U$ _{q} $ , particle-particle field$ \widetilde{\mathit{U}}_{q} $ , Coulomb field U$ _{C}(\mathbf{r}) $ , and abnormal spin-orbit field$ \widetilde{\mathit{B}}_{q} $ ) can be found from Ref. [86].The above fields in matrix form can be written as
$ \begin{array}{*{20}{l}} \mathcal{M}=\left( \begin{array}{cc} M & \widetilde{M} \\ \widetilde{M} & -M \end{array} \right) ,\mathcal{U}=\left( \begin{array}{cc} U-\lambda & \widetilde{U} \\ \widetilde{U} & -U+\lambda \end{array} \right), \end{array} $

(18) $ \mathcal{U}_{so}=\left( \begin{array}{cc} B & \widetilde{B} \\ \widetilde{B} & -B \end{array} \right) \frac{j(j+1)-l(l+1)-\frac{3}{4}}{2r}. $

(19) Finally, the bulk and microscopic properties can be obtained by solving the following SHFB equation in the coordinate representation:
$\begin{aligned}[b]& \left[ -\frac{{\rm d}}{{\rm d}r}\mathcal{M}\frac{{\rm d}}{{\rm d}r}+\mathcal{U}+\mathcal{M}\frac{l(l+1) }{r^{2}}+\frac{\mathcal{M}^{{\prime }}}{r}+\mathcal{U}_{so}\right] \left( \begin{array}{c} u_{1} \\ u_{2} \end{array} \right)\\ =&E\left( \begin{array}{c} u_{1} \\ u_{2} \end{array} \right),\end{aligned} $

(20) where
$\mathcal{M}^{{\prime }}$ is the first order derivative with respect to the radial coordinate r. -
The tensor force has ever been added as a perturbation to existing Skyrme parameterization, for example, SLy5+T parameterization [70]. However, Lesinski et al. pointed out that the tensor force should not be added perturbatively to existing interactions and a complete refit of the entire parameter set is imperative [67]. Therefore, they constructed a set of 36 Skyrme parameterizations, covering a wide range of the parameter space of the isoscalar and isovector tensor term coupling constants with a fit protocol similar to that of the successful SLy parameterizations [67]. The 36 Skyrme parameterizations are known as TIJ (I(J) = 1, 2, 3..., 6) parameterizations, where the indices I and J are related to the coupling constants β and α of Eqs. (13) and (15),
$ \begin{aligned}[b] \alpha =&60(J-2), \\ \beta =&60(I-2). \end{aligned} $

(21) The tensor effect can be shown by the evolution of nuclear structure with I or J.
Based on the above introductions, the specific procedure of this study is as follows. First, nuclei with a
$ 2p $ halo are sought out by calculating the$ 2p $ separation energies ($ S_{2p} $ ) and charge radii ($R _{ch} $ ) of the extremely proton-rich Ne, Mg, Si, S, Ar, and Ca isotopes using the mixed pairing force within 24 sets of the$ TIJ $ (I = 1, 2, 3, 4; J = 1, 2, 3..., 6) parameterizations. Next, the$ \mathcal{J}^{2} $ term tensor effect on the$ 2p $ radioactivity of the$ 2p $ halo nuclei is explored with the selected interactions T1J (J = 1, 2, 3..., 6) and TI1 (I = 1, 2, 3, 4). Finally, the pairing correlation effect on the$ 2p $ radioactivity of the nuclei with a$ 2p $ halo is discussed.To show the tensor feature of the T1J and TI1 interactions clearly, the evolutions of
$B _{s.o.}^{p} $ and$ Q_{2p} $ with the tensor parameter α or β are necessary, which are described in the next paragraphs.From Eq. (15), we can see that
$B _{s.o.}^{p} $ is directly relevant to the$W _{0} $ , α, and β terms. For the T1J interactions, β is not changed. Meanwhile,$ \rho (\mathbf{\pmb r}) $ and J$ _{q} $ (r) are assumed to be constant with different J values for a given nucleus. With these conditions, the$B _{s.o.}^{p} $ increment ($ \Delta B _{s.o.}^{p} $ ) is only determined by the$W _{0} $ increment ($ \Delta W_{0} $ ) and α increment ($ \Delta \alpha $ ),$ \begin{aligned}[b] \Delta B_{s.o}^{p} =&B_{s.o}^{p}\left( T1J\right) -B_{s.o}^{p}\left( T1X\right) ,\left( X<J, J-X=1\right) , \\ =&\frac{1}{2r}\left( W_{0}^{T1J}-W_{0}^{T1X}\right) \left( 2\frac{{\rm d}\rho _{p} }{{\rm d}r}+\frac{{\rm d}\rho _{n}}{{\rm d}r}\right)\\& +\left( \alpha ^{T1J}-\alpha ^{T1X}\right) \frac{J_{p}}{r}, \\ =&\frac{1}{2r}\Delta W_{0}\left( 2\frac{{\rm d}\rho _{p}}{{\rm d}r}+\frac{{\rm d}\rho _{n}}{{\rm d}r }\right) +\Delta \alpha \frac{J_{p}}{r}, \end{aligned} $

(22) where
$B _{s.o.}^{p}\left(T1X\right) $ and$B _{s.o.}^{p}\left(T1J\right) $ represent the proton spin-orbit coupling potentials with the T1X and T1J interactions, respectively.Similarly,
$ \Delta B _{s.o.}^{p} $ with the TI1 interactions can be expressed as$ \Delta B_{s.o}^{p}=\frac{1}{2r}\Delta W_{0}\left( 2\frac{{\rm d}\rho _{p}}{{\rm d}r}+ \frac{{\rm d}\rho _{n}}{{\rm d}r}\right) +\Delta \beta \frac{J_{n}}{r}. $

(23) In addition,
$ Q_{2p} $ is influenced by the$ \mathcal{J}^{2} $ term because$\varepsilon _{\rm Tensor}$ has a certain contribution to the binding energy E of a nucleus, which can be seen from Eqs. (5) and (13). For the T1J interactions, the$ Q_{2p} $ increment ($ \Delta Q_{2p} $ ) with J is written as$ \begin{aligned}[b] \Delta Q_{2p} =&Q_{2p}^{T1J}-Q_{2p}^{T1X}, \left( X<J, J-X=1\right), \\ =&\left( E_{\rm daughter}^{T1J}-E_{\rm parent}^{T1J}\right) -\left( E_{\rm daughter}^{T1X}-E_{\rm parent}^{T1X}\right) , \\ =&\left( E_{\rm parent}^{T1X}-E_{\rm parent}^{T1J}\right) -\left( E_{\rm daughter}^{T1X}-E_{\rm daughter}^{T1J}\right), \end{aligned} $

(24) where
$E_{\rm parent}^{T1X}$ and$ E_{\rm parent}^{T1J} $ are the total binding energies of a parent nucleus with the T1X and T1J interactions, respectively.$E_{\rm daughter}^{T1X}$ and$E_{\rm daughter}^{T1J}$ refer to the total binding energies of a daughter nucleus with the T1X and T1J interactions, respectively.Note that the kinetic energy density k, pairing energy density
$\varepsilon _{\rm Pair}$ , and Coulomb energy density$\varepsilon _{\rm Coul}$ are not relevant to the Skyrme parameterizations [86], and for the T1J interactions, the$ t_{i} $ and$ x_{i} $ (i = 1, 2, 3) values change slightly with increasing J except for the$ W_{0} $ and α values. In this case, the contributions to the terms in the brackets of Eq. (24) from k,$\varepsilon _{\rm Pair}$ , and$\varepsilon _{\rm Coul}$ and the terms that are correlated to$ t_{i} $ and$ x_{i} $ in the Skyrme energy density$\varepsilon _{\rm Skyrme}$ almost cancel each other out. As a result,$ \Delta Q_{2p} $ is determined mainly by the spin-orbit energy density (the$ W_{0} $ term in$\varepsilon _{\rm Skyrme}$ ) and$\varepsilon _{\rm Tensor}$ . Therefore, Eq. (24) is modified to$ \begin{aligned}[b] \Delta Q_{2p} \approx &\frac{1}{2}\left( W_{0}^{T1X}-W_{0}^{T1J}\right) \int {\rm d}^{3}\mathbf{r}\Bigg[ \left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm parent}\\&-\left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm daughter}\Bigg] \\ &+\frac{1}{2}\left( \alpha ^{T1X}-\alpha ^{T1J}\right) \int {\rm d}^{3}\mathbf{r} \Bigg[ \left( J_{p}^{2}+J_{n}^{2}\right) _{\rm parent}\\&-\left( J_{p}^{2}+J_{n}^{2}\right) _{\rm daughter}\Bigg] , \\ =&-\frac{1}{2}\Delta W_{0}\int {\rm d}^{3}\mathbf{r}\Bigg[ \left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm parent}\\&-\left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm daughter}\Bigg] \\ &-\frac{1}{2}\Delta \alpha \int {\rm d}^{3}\mathbf{r}\left[ \left( J_{p}^{2}+J_{n}^{2}\right) _{\rm parent}-\left( J_{p}^{2}+J_{n}^{2}\right) _{\rm daughter}\right]. \end{aligned} $

(25) Similarly, for the TI1 interactions,
$ \Delta Q_{2p} $ originates from the terms$ \Delta W_{0} $ and$ \Delta \beta $ $ \begin{aligned}[b] \Delta Q_{2p} \approx &-\frac{1}{2}\Delta W_{0}\int {\rm d}^{3}\mathbf{r}\Bigg[ \left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm parent}\\&-\left( J\nabla \rho +\sum J_{p}\nabla \rho _{p}\right) _{\rm daughter}\Bigg] \\ &-\frac{1}{2}\Delta \beta \int {\rm d}^{3}\mathbf{r}\left[ \left( J_{p}^{2}+J_{n}^{2}\right) _{\rm parent}-\left( J_{p}^{2}+J_{n}^{2}\right) _{\rm daughter}\right] . \end{aligned} $

(26) -
For all the calculations in this study, the spherical box and mesh sizes are selected as 20 fm and 0.1 fm, respectively. The quasiparticle energies are cut off at 60 MeV. The maximum angular momentum of the quasiparticles j
$ _{\max } $ is set to be$ \dfrac{25}{2}\hbar $ . All calculations converge with these conditions. In the next subsections, we discuss the following three aspects: nuclei with a$ 2p $ halo, the$ \mathcal{J}^{2} $ term tensor effect on the$ 2p $ radioactivity of$ 2p $ halo nuclei, and the pairing correlation effect on the$ 2p $ radioactivity of$ 2p $ halo nuclei. -
First, the
$ S_{2p} $ values of the extremely proton-rich Ne, Mg, Si, S, Ar, and Ca isotopes within the 24 sets of$ TIJ $ parameterizations (I = 1, 2, 3, 4; J = 1, 2, 3..., 6) versus A are shown in Fig. 1. Note that for the O isotopes, the calculated binding energies of their daughter nuclides (C nuclides) are not in agreement with the experimental data. Therefore, in Fig. 1, the$ S_{2p} $ values of the O isotopes are not shown. In Fig. 1, the experimental data [15, 98, 99] shows that$ ^{16} $ Ne,$ ^{18} $ Mg, and$ ^{30} $ Ar are located beyond the$ 2p $ drip-line with negative$ S_{2p} $ values, that is, the three nuclei are unbound. For the unbound nucleus$ ^{18} $ Mg, the four-proton radioactivity was observed recently from its ground state [99]. The decay of the ground state is consistent with two sequential steps of$ 2p $ decay, that is,$ ^{18} $ Mg$ _{\text{g.s.}} \rightarrow ^{16} $ Ne$ _{\text{g.s.}} $ +$ 2p $ followed by$ ^{16} $ Ne$ _{\text{g.s.}} \rightarrow {} ^{14}$ O$ _{\text{g.s.}} $ +$ 2p $ . The$ Q_{2p} $ values of the first and second decay steps are 3.44 MeV and 1.42 MeV, respectively. With the relationship$ Q_{2p} $ =$ -S_{2p} $ , it is easy to find that the experimental$ S_{2p} $ value of$ ^{18} $ Mg is –3.44 MeV, which is marked in Fig. 1 by a red star. The unbound nucleus$ ^{30} $ Ar was identified by the measurement of the trajectories of its in-flight decay products$ ^{28} $ S+p+p [15]. Via analysis of the angular correlations of the fragments, the$ Q_{2p} $ value of the ground state of$ ^{30} $ Ar is determined as 2.25$ _{-0.10}^{+0.15} $ MeV. Hence, its ground state experimental$ S_{2p} $ value is -2.25$ _{-0.15}^{+0.10} $ MeV, which is marked by a black star in Fig. 1. As shown in Fig. 1,$ ^{16} $ Ne and$ ^{18} $ Mg are predicted to be unbound with$ S_{2p} < $ 0 by all the interactions. Moreover, the$ S_{2p} $ values of$ ^{16} $ Ne and$ ^{18} $ Mg extracted from all the Skyrme interactions are in good agreement with the experimental values. However, the calculations with all the interactions reveal that$ ^{24} $ S and$ ^{32} $ Ca are$ 2p $ unbound, and the calculated$ S_{2p} $ values of the S and Ca isotopes within all the interactions have a certain deviation from the extant experimental data.$ ^{22} $ Si is predicted to be an unbound nucleus only within the T14, T15, T16, T25, T26, and T36 interactions. However,$ ^{30} $ Ar is also predicted to be$ 2p $ unbound by other interactions besides the above six interaction types.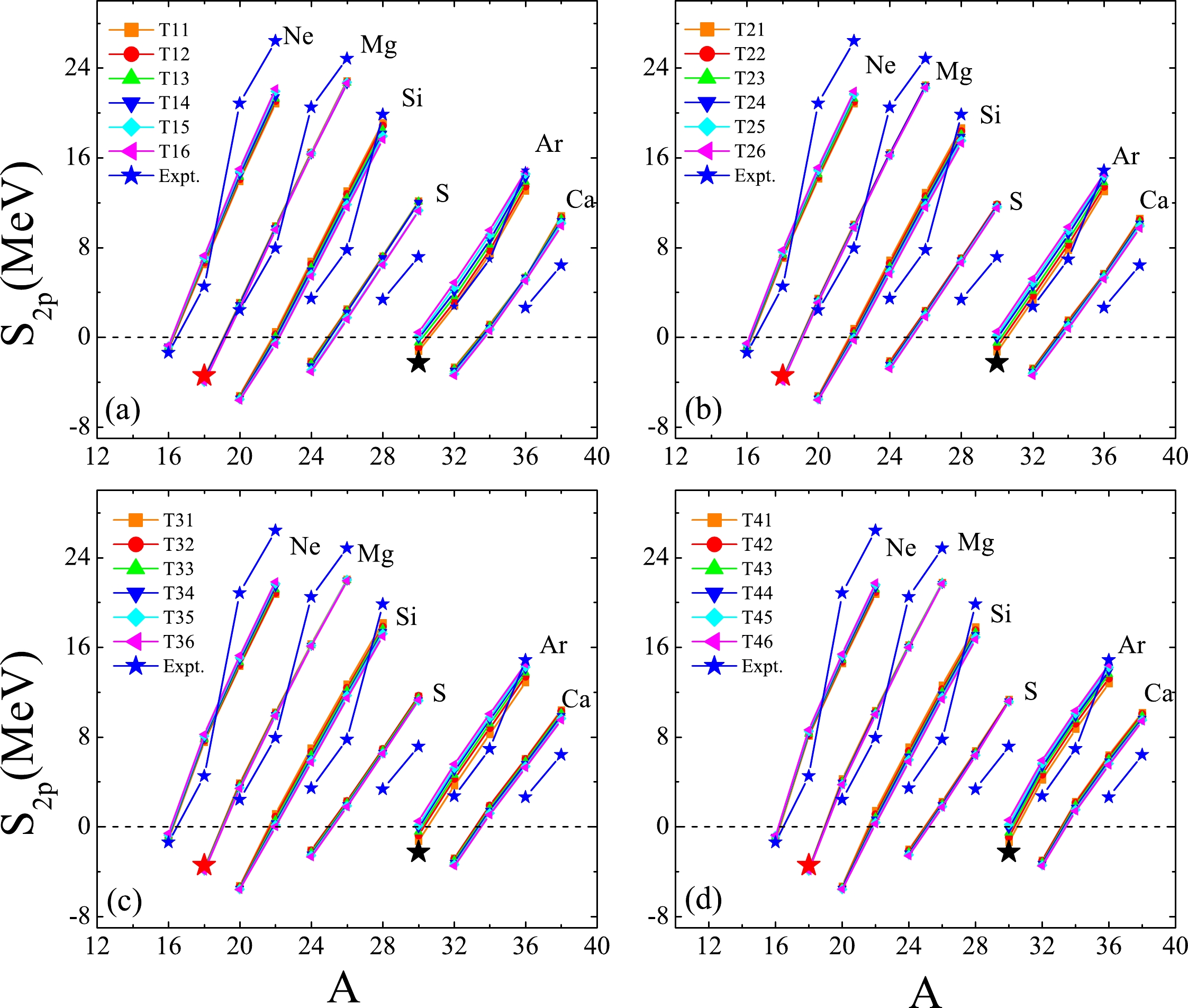
Figure 1. (color online)
$ S_{2p} $ values of the Ne, Mg, Si, S, Ar, and Ca isotopic chains versus the mass number A within the 24 sets of$ TIJ $ interactions (I = 1, 2, 3, 4; J = 1, 2, 3..., 6). The blue stars represent the experimental$ S_{2p} $ values taken from Ref. [98]. The red star is the experimental$ S_{2p} $ value of$ ^{18} $ Mg, which is taken from Ref. [99]. The black star is the experimental$ S_{2p} $ value of$ ^{30} $ Ar taken from Ref. [15].Relevant studies suggest that direct diproton emission may be enhanced by the
$ 2p $ halo because the$ 2p $ halo would lead to a larger spectroscopic factor for a direct diproton decay than that for a sequential decay or a three-body emission [33, 100, 101]. For nuclei with a$ 2p $ halo, the charge density on the nuclear surface is extremely low; therefore, the$ ^{2} $ He cluster preforms more easily under such a condition. As a result, the probability of the direct$ ^{2} $ He emission increases. Recent studies indicate that the$ 2p $ halo plays an important role in diproton emission [56, 102−105]. Therefore, searching for nuclei with a$ 2p $ halo is crucial for the study of$ 2p $ radioactivity. To search for candidates with a$ 2p $ halo, the$R _{ch} $ values of the O, Ne, Mg, Si, S, Ar, and Ca isotopes computed within the 24 sets of$ TIJ $ interactions are shown in Fig. 2. As shown in Fig. 2, the$R _{ch} $ values of$ ^{18} $ Mg and$ ^{20} $ Si are considerably larger than those of the other nuclides for all the interactions. Therefore, it is speculated that$ ^{18} $ Mg and$ ^{20} $ Si may be nuclei with a$ 2p $ halo.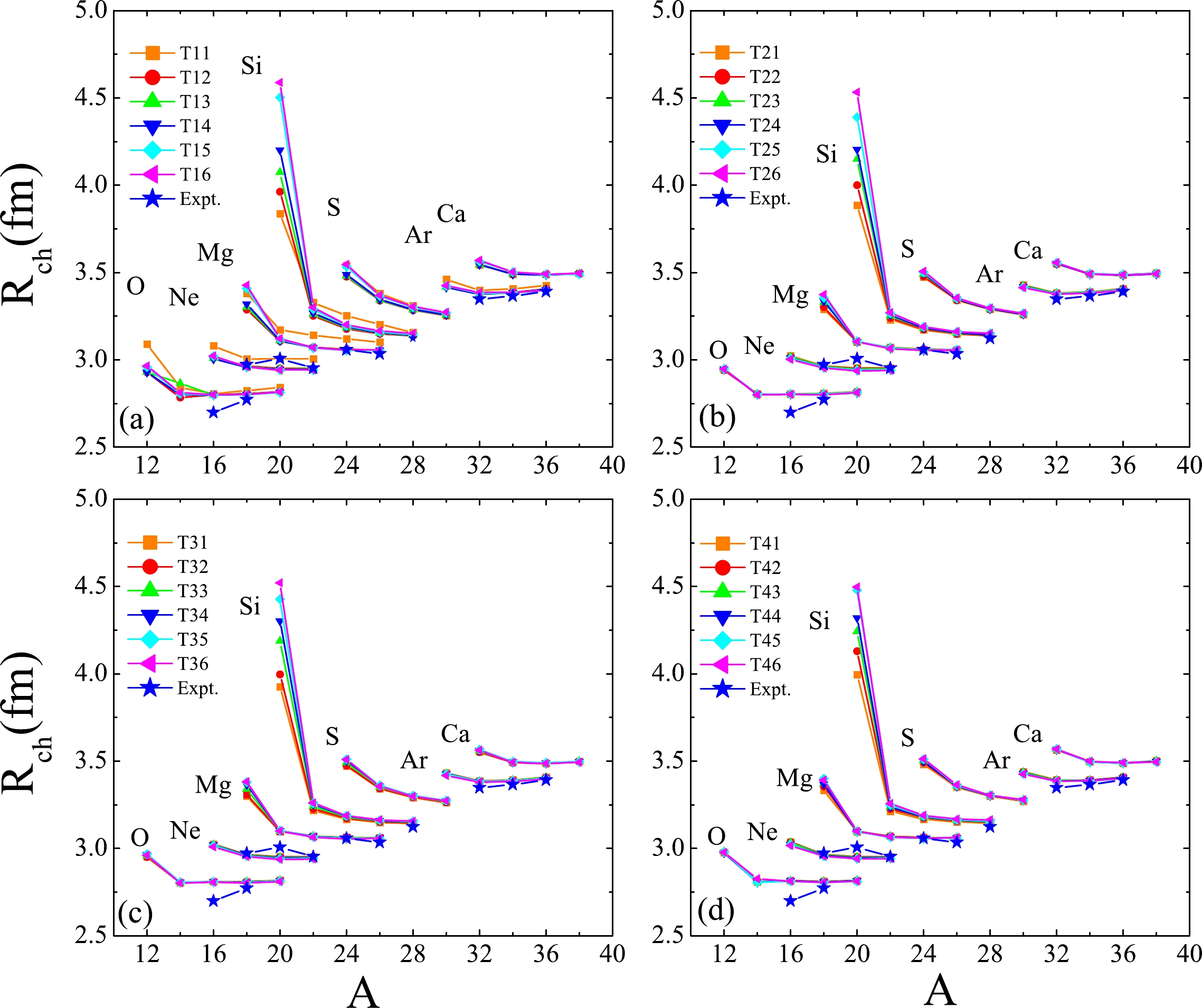
Figure 2. (color online)
$ R_{ch} $ values of the O, Ne, Mg, Si, S, Ar, and Ca isotopes versus A within the 24 sets of$ TIJ $ interactions (I = 1, 2, 3, 4; J = 1, 2, 3..., 6). Meanwhile, in each subfigure,$ R_{ch} $ varies with J, and I remains a constant. The blue stars represent the experimental$ R_{ch} $ values taken from Ref. [106].To further confirm whether the
$ 2p $ halo structure exists in$ ^{18} $ Mg and$ ^{20} $ Si, the deformations of the two nuclei are evaluated using deformed SHFB theory with the T31 interaction, where$ ^{18} $ Mg and$ ^{20} $ Si are found to be nearly spherical. In addition, relevant studies suggest that the$ 2p $ halo-like structure rather than the deformation is responsible for the$ 2p $ correlation and the mechanism of$ 2p $ emission [56, 102−105]. Therefore, with the microscopic single-proton energy spectra obtained within spherical SHFB theory, we can examine the$ 2p $ halo structure of$ ^{18} $ Mg and$ ^{20} $ Si. In Fig. 3, we plot the single-proton energy spectra and relative contributions of different orbits to the full density with the T31 interaction. As shown in Figs. 3(a) and (b), the 2$s _{1/2} $ states of$ ^{18} $ Mg and$ ^{20} $ Si are not only close to the Fermi energies but also located in the region of the resonant states in the continuum. As a result, a certain number of protons occupy the resonant 2$s _{1/2} $ state with a sizable probability owing to the pairing. Furthermore, the contribution of the 2$s _{1/2} $ state to the full density of the large r region is dominant, which can be seen from Figs. 3(c) and (d). Because the centrifugal barrier of the 2$s _{1/2} $ state is zero, the valence protons can tunnel out of the potential barrier and reach the large r region. Then, an extended density tail forms and the$ 2p $ halo appears.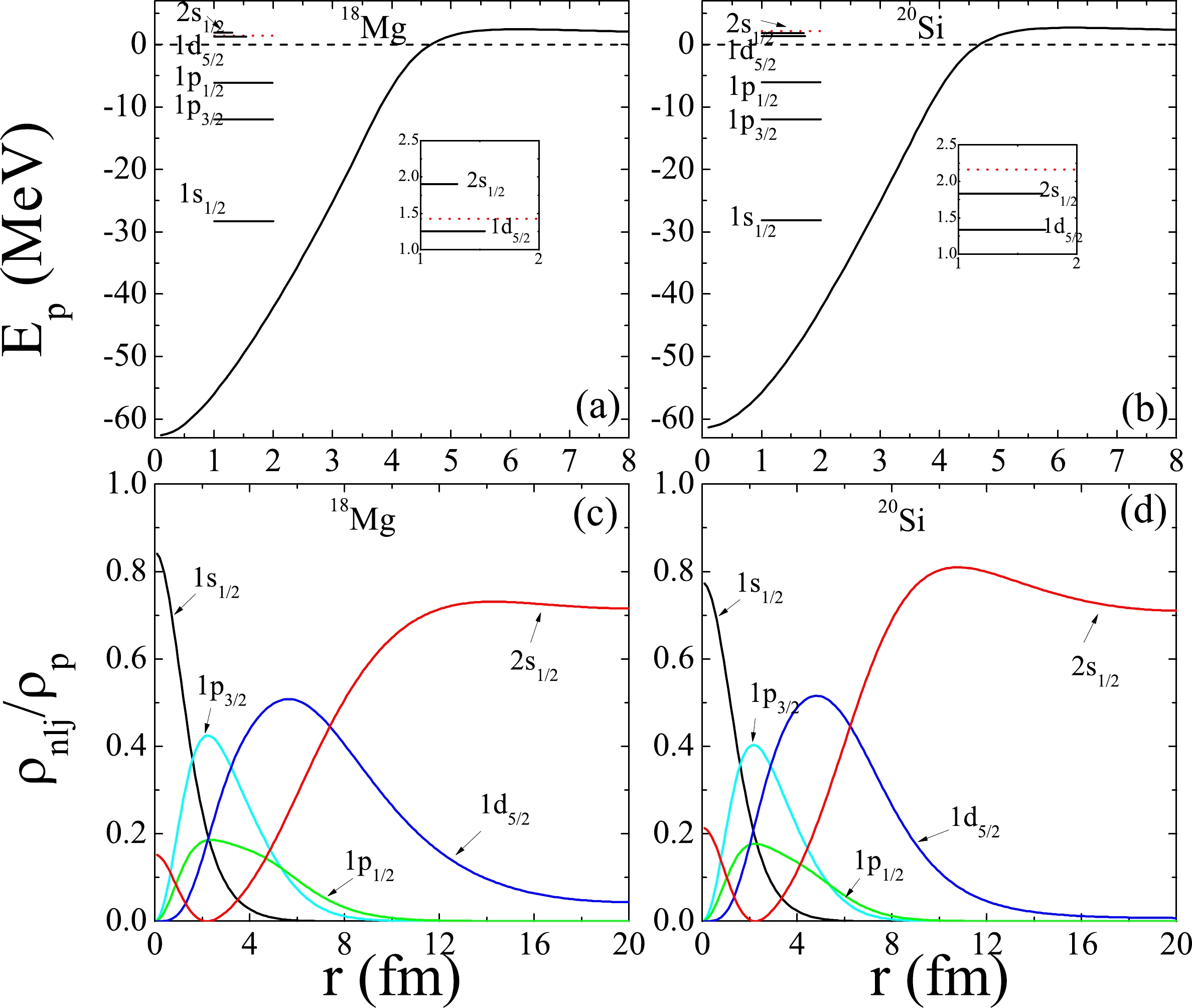
Figure 3. (color online) Upper panel: Single-proton energy spectra and proton mean-field potentials of
$ ^{18} $ Mg and$ ^{20} $ Si within the T31 interaction. Lower panel: Corresponding relative contribution of each orbit to the density as a function of radius. The occupation probabilities of the single-proton levels are proportional to their length. The Fermi energies are depicted by the red dotted lines.Owing to the
$ 2p $ halos of$ ^{18} $ Mg and$ ^{20} $ Si, the$ 2p $ decay type of the two nuclei is speculated as diproton emission in view of Refs. [33, 56, 100, 101] and the speculation of Refs. [102−105]. Moreover,$ ^{12} $ O,$ ^{16} $ Ne,$ ^{24} $ S, and$ ^{30} $ Ar without$ 2p $ halos are preferred to sequential or three-body radioactivity. From the experimental perspective, the reasonableness of the conclusion of Refs. [33, 56, 100, 101] and the speculation of Refs. [102−105] can be tested using the following experimental facts: The$ 2p $ radioactivity of$ ^{12} $ O and$ ^{16} $ Ne was confirmed to be the sequential type by the measurements of Azhari et al. [12]. The measurement of$ 2p $ decay in$ ^{16} $ Ne suggests its$ 2p $ decay type is the sequential one [11, 13]. In$ ^{30} $ Ar [15], a transition interplay of true three-body and sequential$ 2p $ decays was detected from the measured angular correlations of the decay products. Therefore, the predicted$ 2p $ emission modes of$ ^{12} $ O,$ ^{16} $ Ne, and$ ^{30} $ Ar are consistent with those of the measurements. -
According to Eq. (21), the tensor parameters α and β are correlated with the indices J and I, respectively. Therefore, from each subfigure of Fig. 2, the impact of α on
$R _{ch} $ can be observed because J continues increasing and I remains a constant. Moreover, the$ \mathcal{J}^{2} $ term tensor effect of α on$R _{ch} $ of$ ^{20} $ Si is the most evident. By analyzing Eq. (22), the tensor effect on$R _{ch} $ can be understood. In addition, the spin-orbit coupling potentials, single-proton energy spectra, and density distributions of$ ^{20} $ Si within the T1J interactions are displayed in the left panel of Fig. 4.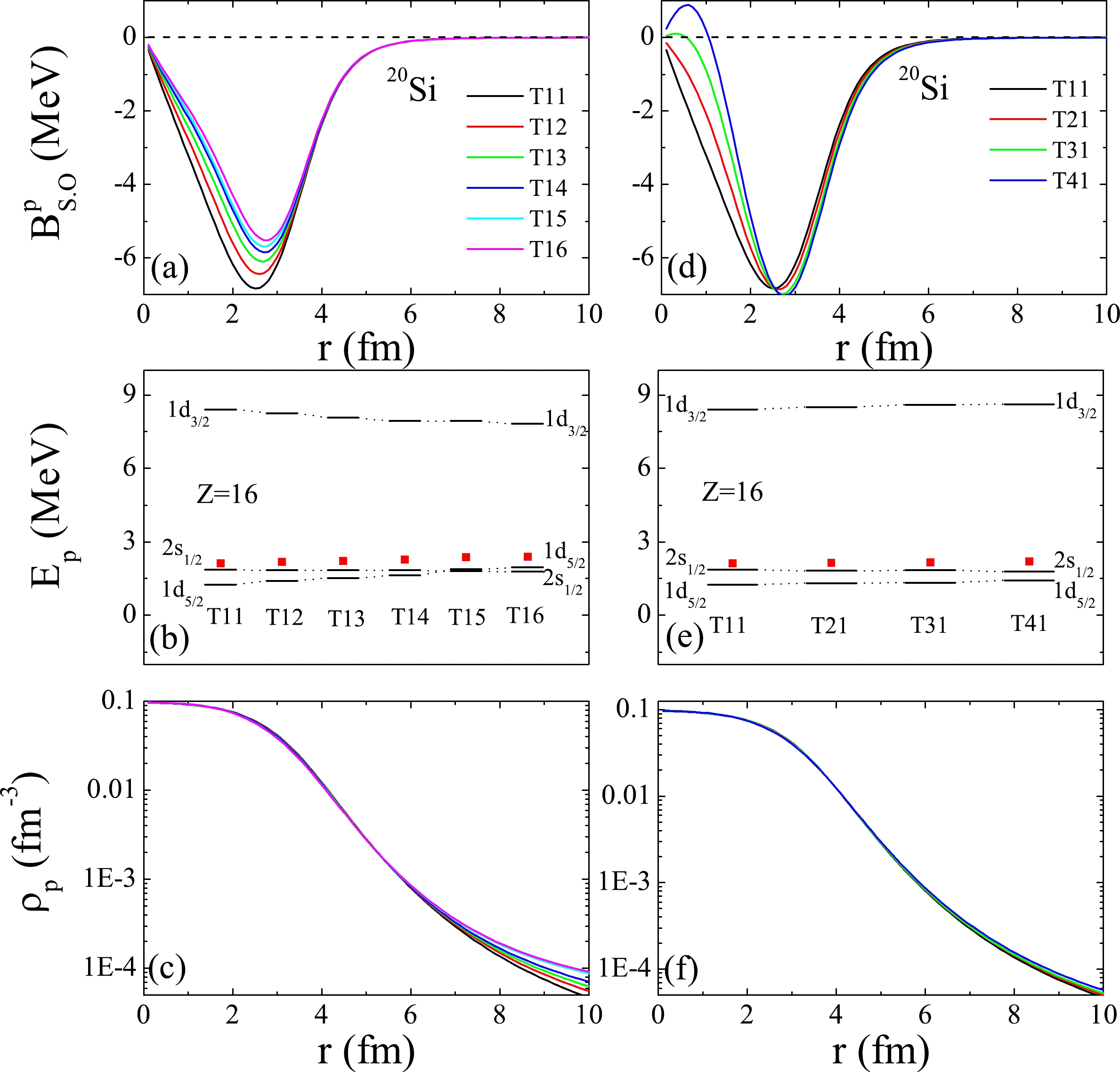
Figure 4. (color online) Proton spin-orbit coupling potentials, single-proton energy spectra, and density distributions of
$ ^{20} $ Si with the T1J (J = 1, 2, 3..., 6) interactions and those with the TI1 (I = 1, 2, 3, 4) interactions. The Fermi energies are depicted by the red solid squares. To observe the evolution of the single-proton energy spectra with J or I clearly, all the single-proton energy levels are of the same length.In Eq. (22),
$ \Delta B _{s.o.}^{p} $ is determined by the$ \Delta W_{0} $ and$ \Delta \alpha $ terms. Table 1 shows the values of$W _{0} $ , α,$ \Delta W_{0} $ , and$ \Delta \alpha $ for different T1J interactions. As shown in Table 1,$ \Delta W_{0} $ and$ \Delta \alpha $ are negative and positive, respectively. Therefore,$ \Delta W_{0} $ makes a negative contribution to$ \Delta B _{s.o.}^{p} $ in Eq. (22). However, the contribution from$ \Delta \alpha $ to$ \Delta B _{s.o.}^{p} $ is positive. Therefore,$ \Delta W_{0} $ and$ \Delta \alpha $ compete with each other. Although$W _{0} $ increases with increasing J, the tensor effect of α is not annihilated in the increasing$W _{0} $ . In this respect, the influence of$ \Delta \alpha $ is stronger than that of$ \Delta W_{0} $ . This effect can be observed from the spin-orbit coupling potentials of$ ^{20} $ Si plotted in Fig. 4(a).Physical quantities T11 T12 T13 T14 T15 T16 $\textit{v}^{2}$ 

0.673 0.721 0.759 0.793 0.865 0.881 $\textit{R}_{ch}$ /fm

3.837 3.963 4.074 4.200 4.501 4.587 $\textit{W}_{0}$ /(MeV fm

$^{5}$ )

−103.738 −112.506 −120.411 −128.506 −136.554 −144.925 α/(MeV fm $^{5}$ )

−60 0 60 120 180 240 $\Delta W_{0}$ /(MeV fm

$^{5}$ )

− −8.768 −7.905 −8.095 −8.048 −8.371 $\Delta \alpha $ /(MeV fm

$^{5}$ )

− 60 60 60 60 60 Physical quantities T11 T21 T31 T41 $\textit{v}^{2}$ 

0.673 0.700 0.707 0.744 − − $\textit{R}_{ch}$ /fm

3.837 3.884 3.924 3.993 − − $\textit{W}_{0}$ /(MeV fm

$^{5}$ )

−103.738 −115.277 −126.989 −138.146 − − β/(MeV fm $^{5}$ )

−60 0 60 120 − − $\Delta W_{0}$ /(MeV fm

$^{5}$ )

− −11.539 −11.712 −11.157 − − $\Delta \beta $ /(MeV fm

$^{5}$ )

− 60 60 60 − − Table 1.
$v ^{2} $ values of the 2$s _{1/2} $ state and the$R _{ch} $ values of$ ^{20} $ Si with the T1J (J = 1, 2, 3..., 6) interactions and those within the TI1 (I = 1, 2, 3, 4) interactions. For each T1J interaction, the$W _{0} $ , α,$ \Delta W_{0} $ , and$ \Delta \alpha $ values are listed, and for each TI1 interaction, the$W _{0} $ , β,$ \Delta W_{0} $ , and$ \Delta \beta $ values are given.As shown in Fig. 4(a), the spin-orbit potential decreases with increasing J, which weakens the splitting of the 1d orbit. For the T15 and T16 interactions, the 1
$d _{5/2} $ orbit exceeds the 2$s _{1/2} $ orbit. These can be observed from Fig. 4(b). Furthermore, with the decrease in the 1d gap, the$v ^{2} $ value of the 2$s _{1/2} $ state is enhanced. The$v ^{2} $ evolution of the 2$s _{1/2} $ state with the T1J interactions can be observed from Table 1, which shows that the$v ^{2} $ value increases from 0.673 with the T11 interaction to 0.881 with the T16 interaction. As a result, the increasing$v ^{2} $ value makes the proton density distribution in a large r region extend progressively further, as shown in Fig. 4(c). Therefore, the$R _{ch} $ values become progressively larger (See Table 1). In other words, the$ 2p $ halo size of$ ^{20} $ Si becomes enhanced with increasing α. Correspondingly, the diproton emission is enhanced with the increase in the$ 2p $ halo size.Similarly, for the TI1 interactions, the tensor effect of β on the
$ 2p $ halo of$ ^{20} $ Si can be explained by Eq. (23) and the right panel of Fig. 4. As shown by Eq. (23), the relationship between$ \Delta W_{0} $ and$ \Delta \beta $ is also competitive. However, the influences on$ \Delta B _{s.o.}^{p} $ from the competitive$ \Delta W_{0} $ and$ \Delta \beta $ are close to each other, which can be observed clearly from Figs. 4(d-f).In Fig. 4(d), the peaks and outer parts of the large r region of the spin-orbit potential are almost the same for different interactions, but only the inner part (in the small r region) increases with increasing I. Hence, the 1d gap changes slightly owing to the similar peaks of the spin-orbit potentials. Nevertheless, 1
$d _{5/2} $ and 1$d _{3/2} $ are shifted up together, which is shown in Fig. 4(e). Consequently, the$v ^{2} $ value of the 2$s _{1/2} $ state is enhanced with increasing I. The$v ^{2} $ values of the 2$s _{1/2} $ state with the T11, T21, T31, and T41 interactions are shown in Table 1. Table 1 shows that the$v ^{2} $ value increases from 0.673 with the T11 interaction to 0.744 with the T41 interaction. Compared with the case of the T1J interactions, the increase in the$v ^{2} $ value within the TI1 interactions is less obvious. Thus, the tail of the density distribution extends slightly, and the corresponding$R _{ch} $ value increases from 3.837 to 3.993 fm (See Fig. 4(f) and Table 1). Therefore, the$ 2p $ halo size and diproton emission of$ ^{20} $ Si are less influenced by β than by α.To observe the
$ 2p $ radioactivity of$ ^{18} $ Mg and$ ^{20} $ Si in future experiments, it is necessary to predict the half-lives within a reliable model. Therefore, the$ 2p $ radioactivity logarithm half-lives$ \log _{10}T_{1/2} $ ($ \log _{10}T_{1/2}=\tau $ ) of the two nuclei are predicted within the effective liquid drop model (ELDM) [25, 107] by inputting the$ Q_{2p} $ values extracted from the 24 sets of TIJ parameterizations and the experimental$ Q_{2p} $ value. These$ Q_{2p} $ and τ values are shown in Table 2. In the framework of the ELDM, the two emitted protons are assumed to be a$ 2p $ -cluster with zero binding energy preforming near the surface of the parent nucleus. Then, the$ 2p $ -cluster penetrates the Coulomb barrier and the two protons separate quickly owing to the dominance of Coulomb repulsion. Within the mechanism of preformation and quantum tunneling, the experimental$ 2p $ radioactivity half-lives are well reproduced [25,107]. To some extent,$ 2p $ radioactivity is similar to α-decay [26−28,107−112]. In Table 2, the$ Q_{2p} $ and τ values of the two nuclei are divided into four groups according to the feature of the TIJ interactions. For each group, the$ Q_{2p} $ and τ values vary with J because I remains a constant. The situation is similar to those of Figs. 1 and 2. As shown in Table 2, the$ Q_{2p} $ values of$ ^{18} $ Mg and$ ^{20} $ Si are relatively large. Moreover, the$ Q_{2p} $ values in any group are impacted less by the tensor parameter J or α, even though the$ Q_{2p} $ evolution with J can be clearly observed. In each group, the$ Q_{2p} $ values become progressively larger with increasing J. Therefore, the two correlated protons inside a nucleus are easier to decay via the mechanism of quantum tunneling.Skyrme interactions $^{18}$ Mg

$^{20}$ Si

Skyrme interactions $^{18}$ Mg

$^{20}$ Si

$Q_{2p}$ /MeV

τ/s $Q_{2p}$ /MeV

τ/s $Q_{2p}$ /MeV

τ/s $Q_{2p}$ /MeV

τ/s 3.44 −18.21 T11 3.62 −18.36 5.19 −18.77 T31 3.71 −18.42 5.27 −18.81 T12 3.69 −18.41 5.29 −18.82 T32 3.72 −18.43 5.32 −18.84 T13 3.73 −18.43 5.37 −18.86 T33 3.81 −18.49 5.43 −18.89 T14 3.78 −18.47 5.44 −18.90 T34 3.86 −18.52 5.49 −18.92 T15 3.97 −18.60 5.53 −18.94 T35 3.90 −18.55 5.55 −18.95 T16 3.98 −18.60 5.62 −18.98 T36 3.95 −18.58 5.58 −18.96 T21 3.67 −18.39 5.23 −18.79 T41 3.78 −18.47 5.30 −18.83 T22 3.71 −18.42 5.32 −18.84 T42 3.83 −18.51 5.38 −18.87 T23 3.78 −18.47 5.41 −18.88 T43 3.87 −18.53 5.45 −18.90 T24 3.79 −18.48 5.44 −18.90 T44 3.88 −18.54 5.49 −18.92 T25 3.87 −18.53 5.54 −18.94 T45 3.92 −18.57 5.57 −18.96 T26 3.96 −18.59 5.60 −18.97 T46 3.93 −18.57 5.58 −18.96 Table 2. Predicted
$ 2p $ radioactivity logarithm half-lives$ \log _{10}T_{1/2} $ ($ \log _{10}T_{1/2}=\tau $ ) of$ ^{18} $ Mg and$ ^{20} $ Si within the ELDM [25, 107] by inputting the experimental$ Q_{2p} $ value and those extracted from the 24 sets of T$ IJ $ interactions. The experimental$ Q_{2p} $ value of$ ^{18} $ Mg [99] is shown in bold.As shown by Eq. (25),
$ \Delta Q_{2p} $ arises from the competition between$ \Delta W_{0} $ and$ \Delta \alpha $ . Moreover, if the contribution from$ \Delta W_{0} $ is dominant,$ \Delta Q_{2p} > $ 0 and$ \Delta \tau < $ 0. The$ Q_{2p} $ and τ evolutions with J in Table 2 belong to this situation. Otherwise,$ \Delta Q_{2p} < $ 0 and$ \Delta \tau > $ 0. In addition, the predicted τ values of$ ^{18} $ Mg and$ ^{20} $ Si within the ELDM are approximately –18 s, although the$ Q_{2p} $ values with any group of the TIJ interactions become progressively larger with increasing J. This indicates that the τ values are not sensitive to the$ Q_{2p} $ variation when the$ Q_{2p} $ values are large, as discussed in our recent study [27, 28]. Because the predicted τ values of the two nuclei from different TIJ interactions are similar, these τ values are useful for guiding experiments on$ 2p $ radioactivity with a new generation of radioactive ion beam facilities, for example, the High Intensity heavy-ion Accelerator Facility of China [113, 114].Similarly, the tensor effect of β on
$ Q_{2p} $ and τ can be discussed by the competition between$ \Delta W_{0} $ and$ \Delta \beta $ in Eq. (26). However, the effect from$ \Delta \beta $ is weaker than that from$ \Delta \alpha $ . -
It has been shown that the
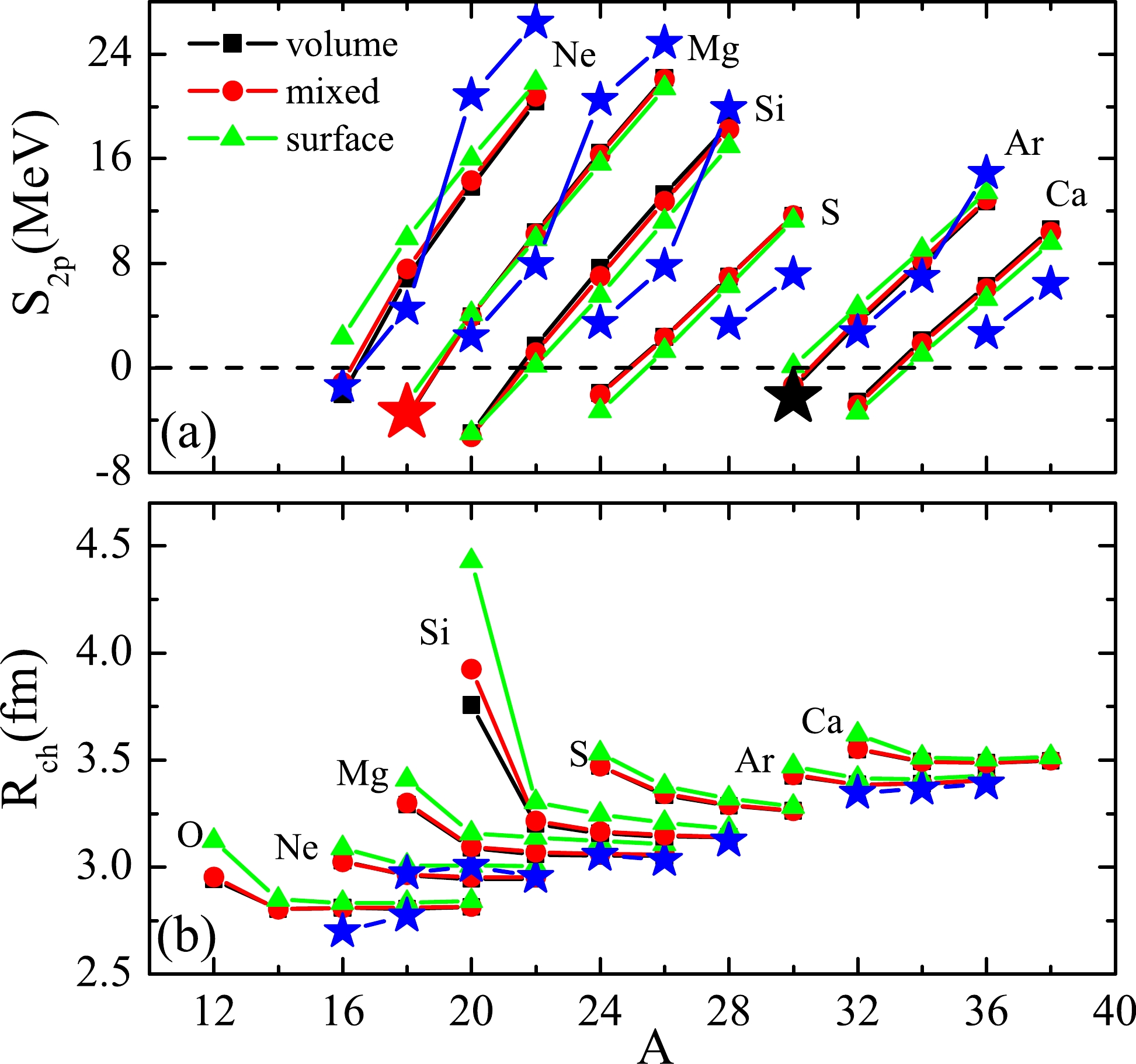
$ 2p $ halo is related to the$v ^{2} $ value of the resonant 2$s _{1/2} $ state in the continuum. Therefore, in practical calculations, the$ 2p $ halo structure may be dependent on the pairing form. In the framework of SHFB theory, the zero range density dependent pairing interaction expressed in Eq. (4) includes the following three types of pairing interactions: volume, surface, and mixed pairing. Hence, it is interesting to investigate how the$ 2p $ halo structure is influenced by different types of pairings. In Fig. 5, we plot the$ S_{2p} $ and$ R_{ch} $ values of the O, Ne, Mg, Si, S, Ar, and Ca isotopic chains with volume, mixed, and surface pairing based on the T31 interaction. As shown in Fig. 5(a),$ ^{16} $ Ne and$ ^{30} $ Ar are predicted to be unbound by volume and mixed pairing. However, the two nuclei are predicted to be bound by surface pairing, which contradicts with the experimental fact that$ ^{16} $ Ne and$ ^{30} $ Ar are unbound nuclei with sequential$ 2p $ radioactivity. It seems that the predictive power of surface pairing is not stronger than those of volume and mixed pairing. Fig. 5(b) shows that the$ R_{ch} $ values of$ ^{12} $ O,$ ^{18} $ Mg, and$ ^{20} $ Si with surface pairing are larger than those with volume and mixed pairing. In particular, for$ ^{20} $ Si, its$ R_{ch} $ value via surface pairing is the largest. The$ R_{ch} $ value from mixed pairing is the second largest, and that from volume pairing is the smallest. This implies that the$ 2p $ halo is greatly enhanced with increased pairing.To understand the
$ 2p $ halo enhancement caused by the increasing pairing, the proton pairing fields$ \widetilde{\mathit{U}}_{p} $ , single-proton spectra, and density distributions of$ ^{18} $ Mg and$ ^{20} $ Si with volume, mixed, and surface pairing based on the T31 interaction are shown in Fig. 6. In addition, in Table 3, we show the$v ^{2} $ values of the 2$s _{1/2} $ state and the$R _{ch} $ values of$ ^{18} $ Mg and$ ^{20} $ Si with the three types of pairings.
Figure 6. (color online) Proton particle-particle fields
$ \widetilde{\mathit{U}}_{p} $ , single-proton energy spectra, and density distributions of$ ^{18} $ Mg and$ ^{20} $ Si with volume, mixed, and surface pairing based on the T31 interaction. All the single-proton energy levels are of the same length, and the Fermi energies are shown by red solid squares.Nuclei Physical
quantitiesVolume
pairingMixed
pairingSurface
pairing$^{18}$ Mg

$\textit{v}^{2}$ 

0.245 0.308 0.323 $\textit{R}_{ch}$ /fm

3.290 3.298 3.410 $^{20}$ Si

$\textit{v}^{2}$ 

0.620 0.707 0.486 $\textit{R}_{ch}$ /fm

3.758 3.924 4.429 Table 3.
$v ^{2} $ values of the 2$s _{1/2} $ state and the$R _{ch} $ values of$ ^{18} $ Mg and$ ^{20} $ Si with volume, mixed, and surface pairing based on the T31 interaction.For
$ ^{18} $ Mg, as shown in Fig. 6(a), the strongest, second strongest, and weakest pairing fields$ \widetilde{\mathit{U}}_{p} $ correspond to surface, mixed, and volume pairing, respectively. With the increase in$ \widetilde{\mathit{U}}_{p} $ , the splitting of the 1d orbit becomes progressively smaller (Fig. 6(b)). As a result, more and more protons occupy the 2$s _{1/2} $ state. Then, the tail of the density distribution becomes progressively longer (Fig. 6(c)). Furthermore, progressively larger$R _{ch} $ values are observed. This can be observed from the$v ^{2} $ values of lines 3-4 in Table 3.For
$ ^{20} $ Si, the situation is similar to that of$ ^{18} $ Mg, which can be observed clearly by comparing the two cases shown in Fig. 6 and Table 3. However, as shown in Table 3, the$v ^{2} $ value of$ ^{20} $ Si with surface pairing is considerably smaller than those within volume and mixed pairing. This special phenomenon is attributed to the 2p intruder orbit. As shown in Fig. 6(e), the 2p$ _{1/2} $ and 2p$ _{3/2} $ orbits appear in the 1d gap. The filled protons in the 2p orbits make a certain contribution to the tail of the density distribution. Furthermore, the$R _{ch} $ value of$ ^{20} $ Si within surface pairing becomes the largest.To observe the pairing correlation effect on
$ Q_{2p} $ , the$ Q_{2p} $ values extracted from volume, mixed, and surface pairing based on the T31 interaction are listed in Table 4. Moreover, we show the corresponding τ values estimated within the ELDM [25, 107] by inputting the$ Q_{2p} $ values extracted from different pairings and the experimental$ Q_{2p} $ value [15, 98, 99]. As shown in Table 4, the$ Q_{2p} $ values of$ ^{18} $ Mg decrease with increased pairing. That is, the$ S_{2p} $ values increase with increased pairing. However, a special$ Q_{2p} $ evolution versus pairing is observed in$ ^{20} $ Si. The$ Q_{2p} $ ($ S_{2p} $ ) value with mixed pairing is larger (smaller) than that with surface pairing. Thus, it is not difficult to discover that increased pairing correlations do not always lead to greater$ S_{2p} $ values and lower chemical potentials to increase nuclear stability. This discovery is different from that of a previous study on the change in the two-neutron separation energies caused by pairing correlations [83].Pairing interactions $^{18}$ Mg

$^{20}$ Si

$Q_{2p}$ /MeV

τ/s $Q_{2p}$ /MeV

τ/s 3.44 −18.21 Volume 3.80 −18.48 4.97 −18.66 Mixed 3.71 −18.42 5.27 −18.81 Surface 2.59 −17.34 4.99 −18.67 Table 4.
$ Q_{2p} $ values extracted from volume, mixed, and surface pairing with the T31 interaction. The τ values are estimated within the ELDM [25, 107] by inputting the$ Q_{2p} $ values extracted from three types of pairings and the experimental$ Q_{2p} $ value. The experimental$ Q_{2p} $ value of$ ^{18} $ Mg [99] is presented in bold.In the above discussions, we mention that the size of the
$ 2p $ halo is enhanced by surface pairing. As a result, the direct diproton emission of$ ^{18} $ Mg and$ ^{20} $ Si may be enhanced by surface pairing, as concluded by previous studies [33, 56, 100−105]. However, in Table 4, the$ Q_{2p} $ values of$ ^{18} $ Mg and$ ^{20} $ Si with surface pairing are smaller than those with mixed pairing. In other words, the smaller$ Q_{2p} $ values caused by surface pairing would lead to larger τ values, which can be clearly found in Table 4. Therefore, the diproton emission of the two nuclei becomes more difficult. Nevertheless, as shown inTables 2 and 4, the τ values of$ ^{18} $ Mg and$ ^{20} $ Si are barely dependent on the$ Q_{2p} $ variations because the$ Q_{2p} $ values are relatively large. Therefore, we can determine the order of magnitude of the$ 2p $ decay half-lives of$ ^{18} $ Mg and$ ^{20} $ Si, which is approximately 10$ ^{-18} $ s. -
In this study, the tensor and pairing correlation effects on the
$ 2p $ halo structure and$ 2p $ radioactivity of$ ^{18} $ Mg and$ ^{20} $ Si are explored in the framework of spherical SHFB theory. In addition, the$ 2p $ radioactivity half-lives of the two$ 2p $ nuclei are predicted within the ELDM. The obtained results allow us to draw the following conclusions:(i) Owing to the competition between the
$ \Delta W_{0} $ and$ \Delta \alpha $ ($ \Delta \beta $ ) contributions to the spin-orbit coupling potential, the$ 2p $ halo size and diproton emission become enhanced with the increase in the tensor parameter α or β. Moreover, the effect from α is stronger than that from β.(ii) The
$ Q_{2p} $ values of$ ^{18} $ Mg and$ ^{20} $ Si are relatively large, and the impact from the$ \mathcal{J}^{2} $ tensor term on the$ Q_{2p} $ values is small. However, the$ Q_{2p} $ values become progressively larger with the increase in the tensor parameter. Further analysis suggests that the$ Q_{2p} $ evolution is originally from the competition between the$ \Delta W_{0} $ contribution to the spin-orbit energy density and the$ \Delta \alpha $ ($ \Delta \beta $ ) contribution to the tensor energy density.(iii) The
$ 2p $ halo size and diproton emission are strongly enhanced by pairing growth because more protons occupy the 2$s _{1/2} $ state. However, for$ ^{20} $ Si, the 2p orbit intrudes into the 1d gap owing to surface pairing. The filled protons in the 2p orbits make a certain contribution to the tail of the density distribution, leading to a$ 2p $ halo with a larger size.(iv) The pairing correlation has a certain influence on the
$ Q_{2p} $ values of$ ^{18} $ Mg and$ ^{20} $ Si. However, the$ Q_{2p} $ values with surface pairing are smaller than those with mixed pairing. As a mechanism of quantum tunneling, the diproton emission becomes more difficult via surface pairing.(v) The weak dependence of the τ values on the
$ Q_{2p} $ variations caused by the$ \mathcal{J}^{2} $ tensor term and pairing correlation is found. Moreover, the order of magnitude of the$ 2p $ radioactivity half-lives of the two nuclei is determined as approximately 10$ ^{-18} $ s.Finally, it is necessary to note that two-neutron (
$ 2n $ ) radioactivity has been an attractive subject in recent years [115−119]. Therefore, it is interesting to explore the tensor force and pairing correlation effects on the$ 2n $ halo and$ 2n $ radioactivity within the Skyrme energy density functional, which is underway. -
We thank professor Jianmin Dong, professor Ligang Cao, professor Shisheng Zhang, and the anonymous reviewers for helpful suggestions and comments.
Roles of tensor force and pairing correlation in two-proton radioactivity of halo nuclei
- Received Date: 2023-02-09
- Available Online: 2023-08-15
Abstract: The tensor force and pairing correlation effects on the two-proton radioactivity of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: