Simple scenario of integrated neutron-proton interaction

Neutron-proton interactions play the most important role in the evolution of the shell structure, collectivity, phase shape transitions, and deformation, as stressed by de Shalit [1] and Talmi [2] and later by Federman and Pittel [3, 4]. The neutron-proton interaction was simplified and parametrized as $N_{p} N_{n}$, i.e., the product of the valence proton number and valence neutron number, by Casten [5]. This is called the $N_{p} N_{n}$ scheme in literature, or in a more semantic meaning, the valence correlation scheme [6, 7]. Zhang and collaborators [8], and later Fu et al. [9], empirically extracted integrated neutron-proton interactions (denoted as $ V_{\rm NP} $) by using the experimental atomic masses, and a remarkable linearity between $ V_{\rm NP} $ and $N_{p} N_{n}$ was shown for the case with $ 50 < Z < 82 $ and $ 50 < N < 82 $. Recently, it was demonstrated [10] that such integrated neutron-proton interactions exhibit systematic differences for the particle-particle, hole-hole, and particle-hole cases in the ($ 50 < Z < 82 $ and $ 82 < Z < 126 $) major shells. This pattern is a reflection of the differences in the average neutron-proton interactions of those three cases, as pointed out earlier by Cakirli and Casten in Ref. [11]. For completeness, we mention Refs. [12–18], in which neutron-proton interactions were also studied from other perspectives.

The purpose of this paper is to provide a simple scenario for the above interesting pattern of integrated neutron-proton interactions. We show that these regularities essentially originate from nuclear symmetry energy, with a subtle effect from the shell correction. We also present a compact formula of $ V_{\rm NP} $ in terms of $N_{n} N_{p}$.

The remainder of this paper is organized as follows. In Sec. II, we derive the formula of $ V_{\rm NP} $ based on the improved liquid-drop model with the shell correction [19]. In Sec. III, we discuss the contributions of the Wigner energy and the shell effect to the $ V_{\rm NP} $, and in Sec. IV, we discuss the linear correlation between $ V_{\rm NP} $ and $N_{p} N_{n}$ as well as the relative magnitudes of the particle-particle, hole-hole, particle-hole, and hole-particle cases. In Sec. V, we summarize this paper.

In this section, we present the values of $ V_{\rm NP} $ extracted by using theoretical binding energies of the WS3 model [19] and compare these empirical results for $ V_{\rm NP} $ with those calculated via our simple formula of $ V_{\rm NP} $ derived from the liquid-drop model with the shell correction. We shall see remarkable consistency between $ V_{\rm NP} $ values obtained via these two approaches.

Let us begin our discussion with the definition of $ V_{\rm NP} $. According to Eqs. (4)–(5) of Ref. [9], the empirical integrated neutron-proton interaction is expressed as follows:

where $\delta_{p}$ ($\delta_{n}$) is $ +1 $ if the valence protons (neutrons) are particle-like and $ -1 $ if the valence protons (neutrons) are hole-like, $ Z_0 $ ($ N_0 $) is the nearest magic number for protons (neutrons), and $ S(Z, N) $ is defined as

where B represents the nuclear binding energy. For convenience, in this paper, we use the convention that the values of B are positive; with this convention, the values of $ V_{\mathrm{NP}} $ are positive.

In Fig. 1, we plot such extracted $ V_{\mathrm{NP}} $ values versus $N_{p} N_{n}$ from the improved Weizsäcker mass formula (WS3) [19] for numerous major shells: ($ 28 < Z < 50 $, $ 28 < N < 50 $), ($ 28 < Z < 50 $, $ 50 < N < 82 $), ($ 50 < Z < 82 $, $ 50 < N < 82 $), and ($ 50 < Z < 82 $, $ 82 < N < 126 $). These empirical neutron-proton interactions are plotted in panels (a-d), with blue color for the particle-particle case, red for the hole-hole case, green for the particle-hole case, and violet for the hole-particle case. One also sees that the extracted $ V_{\mathrm{NP}} $ values have a good linear correlation with $ N_p N_n $ for each case, as was shown in Fig. 1 (c) of Ref. [10]. We note without details that one obtains a similar pattern if one replaces results of Ref. [19] in Fig. 1 (a-d) by using those of Refs. [20] and [21], i.e., the Duflo-Zuker model and the finite-range-liquid-drop model. Below, this pattern is attributed to symmetry energy with the shell correction.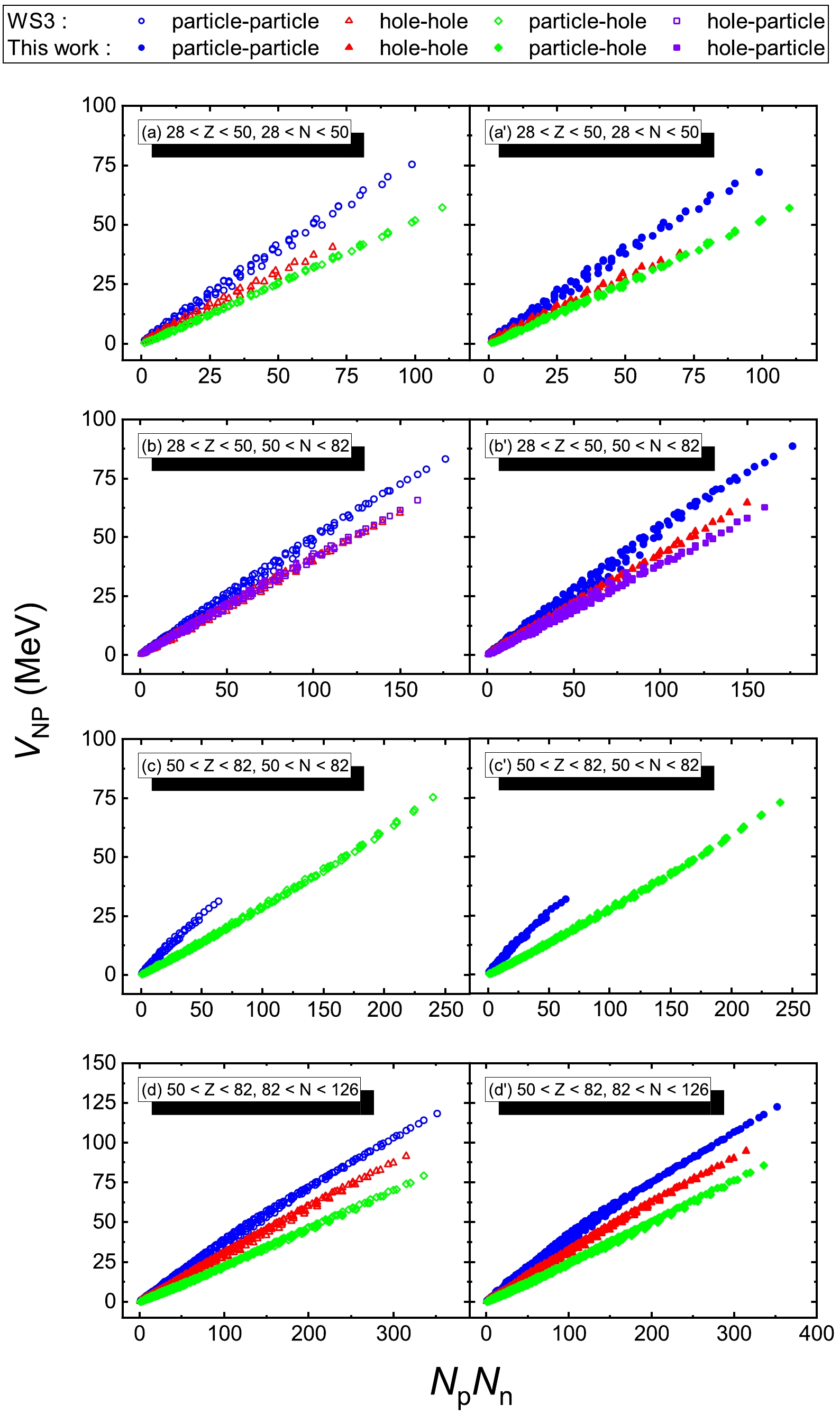

Figure 1.  (color online) $ V_{\mathrm{NP}} $ versus $N_{p} N_{n}$ for the ($ 28 < Z < 50 $, $ 28 < N < 50 $), ($ 28 < Z < 50 $, $ 50 < N < 82 $), ($ 50 < Z < 82 $, $ 50 < N < 82 $),and ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells. Panels (a-d) are extracted from binding energies of Ref. [19] [i.e., the WS3 model] by using Eq. (1), and panels (a$ ' $-d$ ' $) are calculated by using Eq. (16). One sees that the results of these two approaches are consistent with each other. We note without details that one obtains similar results if one replaces results of Ref. [19] by using those of Refs. [20] and [21], i.e., the Duflo-Zuker model and the finite-range-liquid-drop model.

We take the Bethe-Weizsäcker formula in the form of Ref. [19]:

where $ a_{v}, a_{s}, a_{c}, c_{\rm sym}^{\rm V}, c_{\rm sym}^{\rm S} $, and $ a_{\rm pair} $ are coefficients corresponding to the volume energy, surface energy, coulomb energy, volume symmetry energy, surface symmetry energy, and pairing energy, and $ \delta_{np} $ is the same as in Ref. [19]. For these terms, we adopt the same parameters presented in Table I of Ref. [19] (it is noted that variations of these parameters do not change the pattern of this paper, as will be seen below). The last two terms, i.e., $ B_{\rm W} $ and $ B_{\rm shell} $, correspond to the Wigner term and the shell correction term, respectively. One sees easily that the volume energy term is canceled out in Eq. (1) and does not contribute to $ V_{\mathrm{NP}} $. Therefore, in this paper, we skip this term, although it is actually the most important part of the binding energy in the liquid drop model.

We denote the contributions of the surface energy, Coulomb energy, pairing terms, symmetry energy, Wigner energy, and shell correction to $ V_{\rm NP} $ as $ V_{\rm NP}^{\rm surface} $, $ V_{\rm NP}^{\rm Coulomb} $, $ V_{\rm NP}^{\rm pair} $, $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm W} $, and $ V_{\rm NP}^{\rm sh} $, respectively. To proceed with our discussion, we assume $ \dfrac{N_{p}}{Z_0 + N_0} \ll 1 $ and $ \dfrac{N_{n}}{Z_0 + N_0} \ll 1 $. These assumptions are reasonably good unless the mass number $ A= Z+N $ is small; for the four major shells that we discuss in this paper, and particularly for heavy nuclei, these assumptions are applicable.

Now, we show that the sum of these $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm surface} $, $ V_{\rm NP}^{\rm Coulomb} $, and $ V_{\rm NP}^{\rm pair} $ terms yields a linear correlation with $ N_{p} N_{n} $ as the leading order. We note, without details, that these formulas are in unified form for particle-particle, hole-hole, particle-hole, and hole-particle cases, because we take the valence nucleon number to be the number of holes for major shells that are more than half-filled, as indicated by Eqs. (1)–(2).

Because the derivations of $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm surface} $, $ V_{\rm NP}^{\rm Coulomb} $, and $ V_{\rm NP}^{\rm pair} $ are cumbersome, we present the details in Appendix A, except for $ V_{\rm NP}^{\rm sym} $, i.e., the dominant part in $ V_{\rm NP} $. In Eq. (3), the symmetry energy is given by two terms:

Correspondingly, $ V_{\rm NP}^{\rm sym} $ has two terms, which are denoted as $ \left[V_{\rm NP}^{\rm sym}\right]_{V} $ and $ \left[V_{\rm NP}^{\rm sym}\right]_{S} $. By using Eqs. (1)–(2), we obtain

As an approximation, we assume that $ N+Z $, $ N_0+Z_0 $, $ N_0+Z $, and $ N+Z_0 $ plus $ 0 $ ($ 1 $ or $ 2 $) in the denominators on the right-hand side of the above formula are equal to $ \left(N + N_0 + Z + Z_0\right)/2 $. The above $ \left[V_{\rm NP}^{\rm sym}\right]_{V} $ is reduced to

By substituting $N= N_0 +N_{n}$ and $Z= Z_0 + N_{p}$ on the right-hand side of the above formula, we easily obtain

Similarly, one obtains

Therefore, we obtain

Similarly, we obtain

Here, the first term on the right-hand side of Eq. (9) comes from the direct term and the second term comes from the exchange term in the Coulomb energy. According to Fig. 2, the values of $ V_{\rm NP}^{\rm Coulomb} $ are maximally 10 MeV and are far smaller than the values of $ V_{\rm NP}^{\rm sym} $, and more importantly, their values for the particle-particle, hole-hole, particle-hole, and hole-particle cases, are very close to each other. Therefore, the inclusion of this term would not yield any essential differences in the regular pattern of $ V_{\rm NP} $. The values of $ V_{\rm NP}^{\rm surface} $ and $ V_{\rm NP}^{\rm pair} $ are always very small, and we do not consider them below in this paper.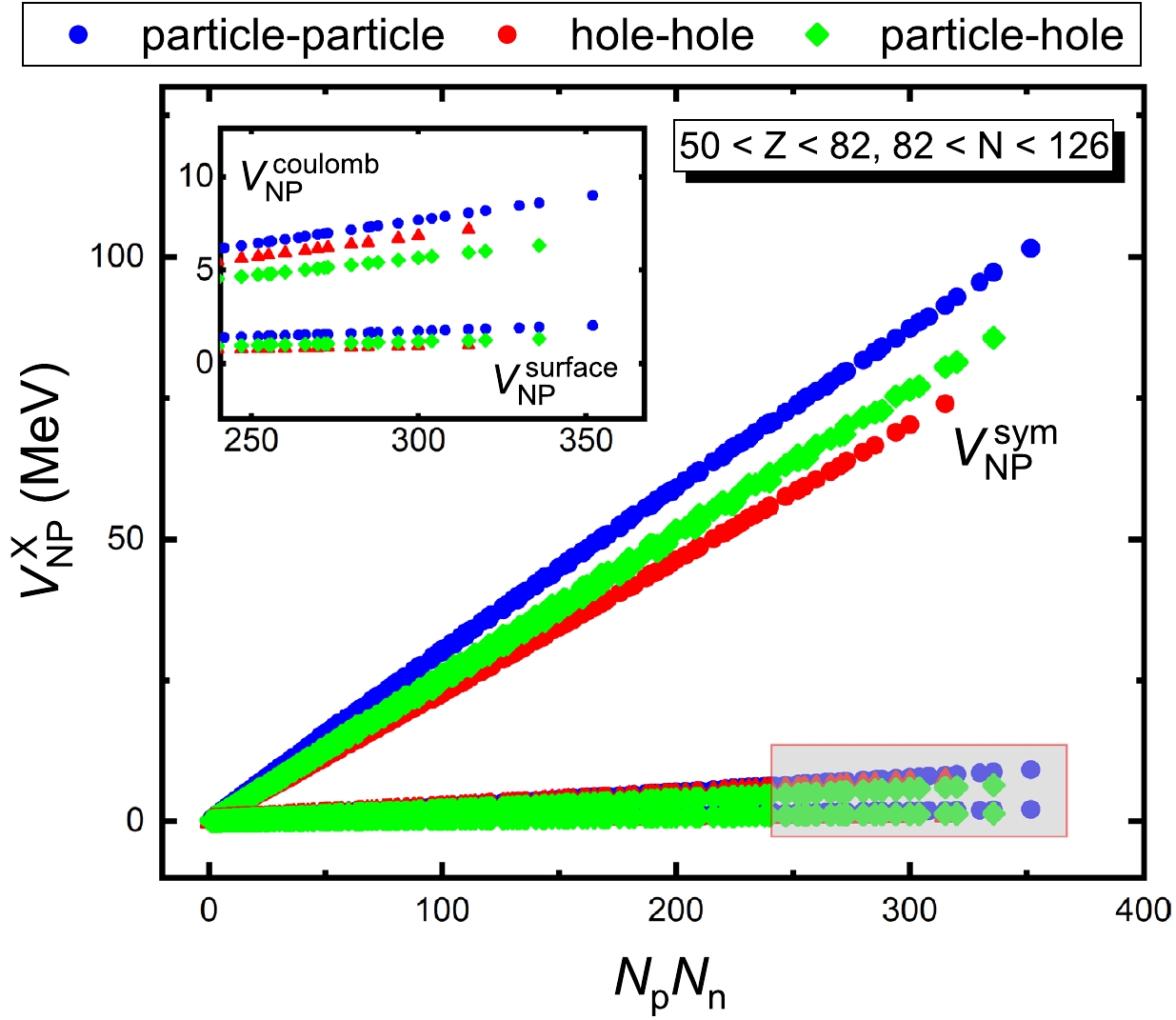

Figure 2.  (color online) $ V_{\rm NP}^{\rm Sym} $, $ V_{\rm NP}^{\rm Surface} $, and $ V_{\rm NP}^{\rm Coulomb} $ calculated by using Eqs. (7)–(9), respectively, versus $N_{p} N_{n}$. We note without details that the magnitude of $ V_{\rm NP}^{\rm pairing} $ is close to zero, and it is omitted here. One sees clearly that the magnitude of $ V_{\rm NP}^{\rm Sym} $ is far larger than those of $ V_{\rm NP}^{\rm Surface} $ and $ V_{\rm NP}^{\rm Coulomb} $.

The results of Eqs. (7)–(10) are very interesting, because all these contributions to the integrated neutron-proton interaction, which originated from the symmetry, surface, Coulomb and pairing energies in the mass formula of the liquid-drop model, are dominantly linear versus $ N_{p} N_{n} $. This provides us with a simple explanation of the good correlation between $ V_{\rm NP} $ and $ N_{p} N_{n} $, which was explored in the literature [8–10].

In Fig. 2, we plot $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm surface} $, and $ V_{\rm NP}^{\rm Coulomb} $ for the case of the major shells of $ 82 < N < 126 $ and $ 50 < Z < 82 $. $ V_{\rm NP}^{\rm pair} $ is not plotted, because its value is always close to zero. From this figure, one sees that the contribution of $ V_{\rm NP}^{\rm sym} $ is dominant, while the two other contributions, i.e., those of $ V_{\rm NP}^{\rm Coulomb} $ and $ V_{\rm NP}^{\rm surface} $, are far smaller. In fact, the relevance measurement of these terms can be clearly seen from Eqs. (7)–(10), where the ratios to $N_{p} N_{n}$ for $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm surface} $, $ V_{\rm NP}^{\rm Coulomb} $, and $ V_{\rm NP}^{\rm pair} $, are approximately proportional to $ 1/A $, $ 1/A^{4/3} $, $ 1/A^{4/3} $, and $ 1/A^{7/3} $, respectively.

In this section we discuss contributions from other two "residual" terms of binding energy in the liquid drop model: the Wigner energy term and the shell correction term in Eq. (3).

The contribution to $ V_{\rm NP} $ from the Wigner energy is sizable only for the particle-particle or hole-hole case with valence protons and neutrons in the same major shells; otherwise, this contribution is very small and is negligible (mostly below 1 MeV) in comparison with the value of $ V_{\rm NP} $, similar to the situation of $ V_{\rm NP}^{\rm pair} $, and this is the case for the ($ 50 < Z < 82 $, $ 82 < N < 126 $) shell. In this paper, for the sake of completeness, we investigate the particle-particle or hole-hole case with valence protons and neutrons in the same major shells.

We assume that $ (N_p + N_n)/(N+Z) $ is small and expand the contribution from the Wigner energy in terms of this ratio. For simplicity, we adopt the Wigner energy from Ref. [22]:

where $ W = 42.7 $ MeV and $ d=28.7 $ MeV, according to Ref. [22]. We note that the results are very close to those obtained by assuming the Wigner energy of Refs. [19], without details. Here, $\pi_{np}$ equals 1 for odd-odd nuclei and vanishes otherwise.

Correspondingly, the contribution to $ V_{\rm NP} $ from the Wigner energy has two terms, which are denoted as $ V_{\rm NP}^{\rm W} $ and $V_{\rm NP}^{d}$, respectively. The result of $V_{\rm NP}^{d}$ is simple and takes the following form. When N and Z are even and $ N = Z $,

and when N and Z are odd and $ N = Z $,

$V_{\rm NP}^{d}$ vanishes otherwise. From these results, one easily sees that $V_{\rm NP}^{d}$ is negligibly small in comparison with the value of $ V_{\rm NP} $ in all the regions that we discuss in this paper. For simplicity, one assumes $V_{\rm NP}^{d} \approx 0$. The details of deriving $ V_{\rm NP}^{\rm W} $ are presented in Appendix A of this paper, and the final results are as follows. When the proton and neutron are in the same major shells,

for the particle-particle case and

for the hole-hole case [in Eq. (15), $N_{p}$ and $N_{n}$ correspond to the numbers of holes]. According to the above two formulas, $ V_{\rm NP}^{\rm W} $ is proportional to $N_{p}$ (or $N_{n}$) when $N_{p}$ (or $N_{n}$) is smaller than $N_{n}$ (or $N_{p}$). Although the $ V_{\rm NP}^{\rm W} $ values in Eqs. (14)–(15) are not well linear-correlated with $N_{p} N_{n}$, they increase as $N_{p}$ and/or $N_{n}$ increase. Furthermore, the values of $ V_{\rm NP}^{\rm W} $ are maximally approximately 10 MeV for the particle-particle and hole-hole cases when the proton and neutron are in the same major shell and thus are far smaller than $ V_{\rm NP}^{\rm sym} $. In principle, $ V_{\rm NP}^{\rm W} $ breaks the linearity between $ V_{\rm NP} $ and $N_{p} N_{n}$ in these two special cases, but this breaking is minor. We note again that the contribution of the Wigner energy to $ V_{\rm NP} $ is negligible when one investigates the ($ 28 < Z < 50 $, $ 50 < N < 82 $) and ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells, in which cases valence protons and neutrons are not in the same major shells.

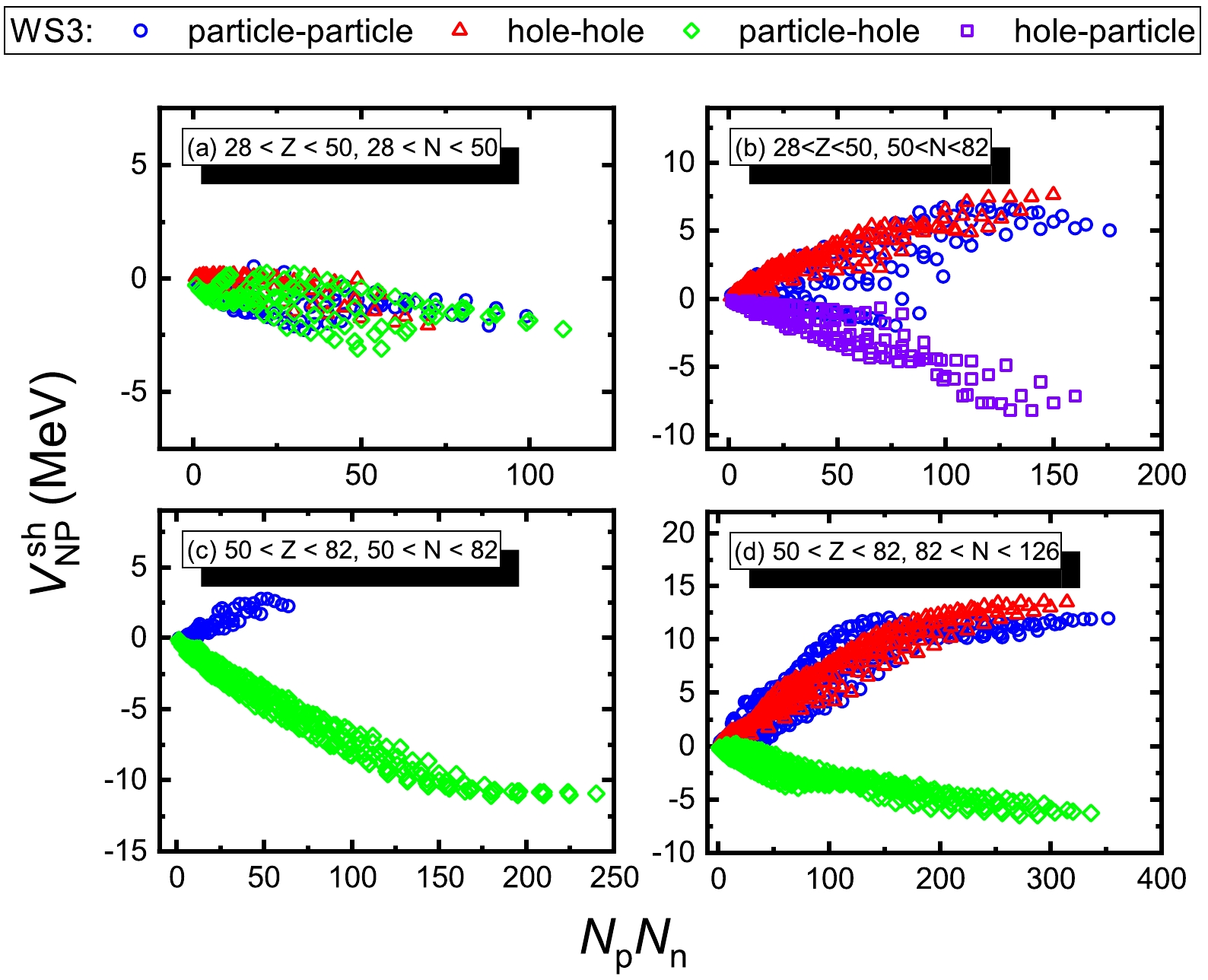
We finally come to the $ V_{\rm NP}^{\rm sh} $ term, by adopting the calculated $ B_{\rm shell} $ of Ref. [19]. The results for $ V_{\rm NP}^{\rm sh} $ are plotted in terms of $N_{p}N_{n}$ in Fig. 3. One sees that these $ V_{\rm NP}^{\rm sh} $ values exhibit reasonable linearity with $N_{p} N_{n}$ in most cases (with fluctuations), with the exception of the ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells in which the magnitudes of $ V_{\rm NP}^{\rm sh} $ increase when $N_{p} N_{n}$ is below 100 and tend to be saturated when $N_{p} N_{n}$ is larger than 100. However, all these $ V_{\rm NP}^{\rm sh} $ values are far smaller than the corresponding $ V_{\rm NP}^{\rm sym} $ results. Additionally, the $ V_{\rm NP}^{\rm sh} $ values of the hole-hole case are maximally approximately 12 MeV (positive), and those of the particle-hole case are maximally approximately 7 MeV (negative). We shall see soon that the sizable differences of $ V_{\rm NP}^{\rm sh} $ between the hole-hole case and particle-hole (hole-particle) case are very important for explaining the subtle pattern of $ V_{\rm NP} $ versus $N_{p}N_{n}$, as observed in Refs. [10, 11].

Figure 3.  (color online) The contribution to $ V_{\rm NP} $ from the shell correction part in the liquid drop model, for four major shells. Here, the shell correction energies are taken from the WS3 model.

In this section, we discuss the implication of our derived formula for $ V_{\rm NP} $.

By summing all the above results of Eqs. (7)–(15), neglecting contributions from the Coulomb energy and pairing interaction [when one discusses the ($ 28 < Z < 50 $, $ 50 < N < 82 $) and ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells, the term $ V_{\rm NP}^{\rm W} $ is also negligible], the neutron-proton interactions are essentially given by

By using Eq. (16), $ V_{\rm NP}^{\rm sym} $ of Eq. (7), the $ V_{\rm NP}^{\rm sh} $ extracted by the shell correction results of Ref. [19], and $ V_{\rm NP}^{\rm W} $ of Eqs. (14) and (15), we obtain $ V_{\rm NP} $ and plot it versus $N_{p} N_{n}$ in panels (a$ ' $-d$ ' $) of Fig. 1(labeled as "this work"). One sees good agreement with the results in panels (a-d).

It is interesting and also one of the purposes of this paper to explain subtle details of the pattern exhibited in Fig. 1. This pattern is very striking and well-known for nuclei in the ($ 28 < Z < 50, 50 < N < 82 $) and ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells, for which Eq. (16) is reduced to

assuming that both $ V_{\rm NP}^{\rm Coulomb} \sim 0 $ and $ V_{\rm NP}^{\rm W} \sim 0 $. Because the ratio of $ V_{\rm NP}^{\rm sym} $ to $N_{p} N_{n}$ is dominantly of $ 1/A $-dependence according to Eq. (7), the neutron-proton interaction is strongest for the particle-particle case, for which the mass number is the smallest among the four cases, i.e., particle-particle, particle-hole, hole-particle, and hole-hole. One therefore expects the ordering of $ V_{\rm NP} $ as follows. The $ V_{\rm NP} $ of the particle-particle case is the largest, that of the hole-hole case is the smallest, and that of the particle-hole and hole-particle cases is in-between.

Interestingly, the above simple pattern is actually "refined", albeit slightly, by the $ V_{\rm NP}^{\rm sh} $ term. This refinement is striking in particular for the ($ 28 < Z < 50 $, $ 50 < N < 82 $) and ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells. As shown in Fig. 3 and discussed in Sec. III, the $ V_{\rm NP}^{\rm sh} $ values are positive for both the particle-particle and hole-hole cases and are negative for both the hole-particle and particle-hole cases. Therefore, the neutron-proton interactions for the particle-particle case is further enhanced by $ V_{\rm NP}^{\rm sh} $ and thus is the largest among the four cases, i.e., the particle-particle, hole-hole, particle-hole, and hole-particle cases. For the particle-hole case and the hole-hole case of the ($ 50 < Z < 82 $, $ 82 < N < 126 $) major shells, although the $ V_{\rm NP}^{\rm sym} $ results of the hole-hole case are the smallest, they are "lifted" up by approximately 12 MeV maximally, while the $ V_{\rm NP}^{\rm sym} $ results of the particle-hole case are reduced by maximally approximately 7 MeV. This competition is the key to explain the order inversion of $ V_{\rm NP} $ for the particle-hole and hole-hole cases. It is the term $ V_{\rm NP}^{\rm sh} $ that reduces $ V_{\rm NP} $ for the particle-hole case and boosts $ V_{\rm NP} $ for the hole-hole case, thus yielding the order inversion of $ V_{\rm NP} $ for these two cases. This is precisely the pattern reported in Refs. [10, 11].

To summarize, in this paper, we study the patterns of neutron-proton interactions (denoted by $ V_{\rm NP} $) in a few major shells of the nuclide chart: ($ 28 < Z < 50 $, $ 28 < N < 50 $), ($ 28 < Z < 50 $, $ 50 < N < 82 $), ($ 50 < Z < 82 $, $ 50 < N < 82 $), and ($ 50 < Z < 82 $, $ 82 < N < 126 $). We show that the dominant part in $ V_{\rm NP} $ originates from the symmetry energy, whose contribution is approximately proportional to $N_{p} N_{n}$, i.e., the product of the valence proton number and valence neutron number. We note without details that this pattern is robust; i.e., one obtains essentially the same pattern if one replaces results of Ref. [19] by using those of Refs. [20] and [21], i.e., the Duflo-Zuker model and the finite-range-liquid-drop model.

Contributions to the $ V_{\rm NP} $ from other parts in the liquid-drop model, such as the volume energy, surface energy term, and Coulomb energy term, are either zero or close to zero. The contribution from the Wigner energy is either very close to zero (when valence protons and neutrons are not in the same major shells) or far smaller than that from the symmetry energy term. The $ V_{\rm NP} $ values of these origins are demonstrated to be the largest for the particle-particle case and the smallest for the hole-hole case. However, the contribution to the $ V_{\rm NP} $ from the shell correction is positive for particle-particle and hole-hole cases and is negative for particle-hole and hole-particle cases. Therefore one has always the strongest $ V_{\rm NP} $ of the particle-particle case for all major shells. The competition of $ V_{\rm NP}^{\rm sym} $, which is the smallest for the hole-hole case and in-between for the particle-hole and hole-particle cases, with $ V_{\rm NP}^{\rm sh} $, which is positive for the hole-hole case and negative for the particle-hole and hole-particle cases, yields an order inversion of $ V_{\rm NP} $ for the hole-hole and particle-hole cases, as observed in previous papers [10, 11].

In the Appendix, we present the details to derive Eqs. (8)–(10), (14), and (15). We exemplify the derivations of the four cases, i.e., the particle-particle, hole-hole, particle-hole, and hole-particle cases, by using the particle-particle case only, as it would be redundant and tedious to present all four cases. The formulas for the other three cases can be obtained in the same way, and with the same form. The particle-particle case corresponds to $\delta_{p} = \delta_{n} = 1$ in Eq. (1). The contributions of the different components to $ V_{\rm NP} $, including $ V_{\rm NP}^{\rm sym} $, $ V_{\rm NP}^{\rm surface} $, $ V_{\rm NP}^{\rm Coulomb} $, $ V_{\rm NP}^{\rm pair} $, and $ V_{\rm NP}^{\rm W} $, include 16 terms, according to the definition of the empirical $ V_{\rm NP} $ in Eqs. (1)–(2). In Sec. II, we present the derivation of $ [V_{\rm NP}^{\rm sym}]_V $.

We first come to the $ V_{\rm NP}^{\rm surface} $ term, with the surface energy of the mass formula defined by $ -a_sA^{\frac{2}{3}} $. From the definition of $ V_{\rm NP} $ in Eqs. (1)–(2), we have

By using the convention $ A_0 = N_0 + N_0 $, $Z= Z_0 + N_{p}$, and $N = N_0 + N_{n}$, the above formula is rewritten as follows:

We expand the right-hand side of $ V_{\rm NP}^{\rm surface} $ in terms of $N_{p}/{A_0}$ and $N_{n}/{A_0}$ and obtain

This gives Eq. (8).

We next come to the contribution of Coulomb energy to $ V_{\rm NP} $. We use the Coulomb energy in the mass formula to be $ -a_c\frac{Z^2}{A^{\frac{1}{3}}}\left(1-0.76Z^{-\frac{2}{3}}\right) $. Here, the contribution from the first term is called the direct term, which is denoted as$ \left[V_{\rm NP}^{\rm Coulomb}\right]_{\rm d} $. As in $ V_{\rm NP}^{\rm surface} $, $ \left[V_{\rm NP}^{\rm Coulomb}\right]_{\rm d} $ has also 16 terms and can be written as follows.

We expand all these terms in terms of $\dfrac{N_{p}}{A_0}$ and $\dfrac{N_{n}}{A_0}$, yielding

This gives the first term of Eq. (9). The second term in Eq. (9) is obtained in the same way.

In Eqs. (1)–(3), the definition of the pairing energy is

Here, $ \delta_{np} $ is defined as

with isospin asymmetry $ I = \left(N-Z\right)/A $. As an approximation, we assume that $ (N+Z+1)^{1/3} $ and $ (N+Z+1)^{1/3} $ are equal to $ (N+Z)^{1/3} $; $ \dfrac{N-Z}{N+Z+2} $ and $ \dfrac{N-Z+1}{N+Z+1} $ are equal to $ \dfrac{(N-Z)}{N+Z} $, and to exemplify the derivation of $ V_{\rm NP}^{\rm pair} $ with $ N > Z $ and both (Z, N) odd, we have

This gives Eq. (10) for the $ N > Z $ case. In all cases of Eq. (23), $ V_{\rm NP}^{\rm pair} $ is negligibly small in the $ V_{\rm NP} $-$N_{p} N_{n}$ plot.

The Wigner energy is defined in Eq. (11). The contribution to the $ V_{\rm NP} $ from the second term is very simple and is given by Eqs. (12)–(13). The contribution from the first term, i.e., $ - W \dfrac{|N-Z|}{A} $, has 16 terms, which can be simplified by using the assumption that $ N+Z $, $ N_0+Z_0 $, $ N_0+Z $, and $ N+Z_0 $ plus $ 0 $ or $ 1 $ or $ 2 $ in the denominators equal $ \left(N + N_0 + Z + Z_0\right)/2 $. We have

In most cases, $ N-Z \gg 1 $, and under this assumption, one has

Clearly, as expected, when valence protons and neutrons are not in the same major shells or when valence protons and neutrons are in the same major shells for the particle-hole and hole-particle cases, $ V_{\rm NP}^{\rm W} $ and $ V_{\rm NP}^{\rm W} $ equal zero in the above formula (in the realistic case, they are very close to zero). For the particle-particle case with valence protons and neutrons in the same major shells, one has

for the hole-hole case with valence protons and neutrons in the same major shells,

The above two formulas give Eqs. (14)–(15).