-
The discovery of the Higgs boson at the Large Hadron Collider (LHC) marked a significant success for the standard model (SM) of particle physics [1, 2]. However, the existence of dark matter (DM), which has been revealed by many astrophysical and cosmological observations, clearly shows that the SM is not a complete theory and the new physics (NP) beyond the SM must exist [3, 4]. Under the assumption that DM is an unknown particle, its properties would be effectively detected at colliders, particularly when its mass is smaller than the center of mass energy of the collider. If this is not the case, the properties of DM might also be investigated through the loop effects at the proposed electron-positron colliders owing to their high precision, such as the Circular Electron Positron Collider (CEPC) [5], Future Circular Collider [6], and International Linear Collider [7].
Among various DM candidates proposed in the literature, weakly interacting massive particles (WIMPs) are very compelling because they can naturally explain the DM relic density (dubbed WIMP miracle). It is natural to construct a WIMP model by introducing a dark sector containing electroweak (EW)
${S U}(2)_L$ multiplets, such as the minimal DM model [8], which involves one nontrivial${S U}(2)_L$ multiplet and is considered the minimal extension. In this paper, we focus on a type of DM model that contains more than one EW multiplet:● Singlet-doublet fermionic dark matter (SDFDM) model: the dark sector involves one singlet Weyl spinor and two doublet Weyl spinors [9–13];
● Doublet-triplet fermionic dark matter (DTFDM) model: the dark sector involves two doublet Weyl spinors and one triplet Weyl spinor [11–14].
Because the even dimensional representation of the
$S U(2)$ group is pseudoreal, two doublet Weyl spinors are introduced to generate the corresponding mass terms. After EW symmetry breaking (EWSB), the Yukawa terms result in mixing between these multiplets. Specifically, the SDFDM (DTFDM) model contains three neutral Majorana fermions and one (two) charged fermions. With a discrete$ Z_2 $ symmetry, the lightest Majorana fermion is stable and can be the DM candidate. Considering the possible couplings between dark sector particles and the gauge bosons (e.g., W, Z, and γ) or Higgs boson, the CEPC is an ideal tool to explore these models because of its accurate measurement and large luminosity.According to it operation plan [5], the CEPC will operate in three possible modes: the Higgs factory, Z factory, and
$ WW $ threshold scan. For the Higgs factory period, the CEPC will run at$ \sqrt{s}=240 $ GeV for$ e^+ e^- \to Z h $ production, and the total integrated luminosity can reach$ \sim 5.6\; {{\rm{ab}}}^{-1} $ [5]. As a result, the CEPC can collect$ \sim 10^6 $ Higgs bosons,$ \sim 10^7 \mu^+\mu^- $ events,$ \sim 3 \times 10^6 ZZ $ events,$ \sim 5 \times 10^7 W^+ W^- $ events, and$ \sim5\times 10^7 Z\gamma $ events. With such many events, the sensitivities of these channels at the CEPC could reach a sub-percentage level. Therefore, the hint of NP could be detected through the loop order processes [12, 15–21]. Some recent studies have investigated such effects in the Higgs decay [22, 23], EW oblique parameters [11, 24],$ e^+ e^- \to W^+ W^- $ [25, 26],$e^+ e^- \to \mu^+ \mu^-$ [27–29], etc.In our paper, we investigate the loop effects of the SDFDM and DTFDM models at the CEPC with
$ \sqrt{s}= 240 $ GeV through five processes:$ e^+e^- \to \mu^+ \mu^-, \; Zh, \; W^+W^-, \; ZZ $ , and$ Z \gamma $ . We calculate the deviations of the cross sections of these processes that are induced by the NP sector at one-loop level and provide the combined CEPC constraints at the 95% confidence level. The results show that the constraints of these five processes can be complementary to each other in some parameter regions. Note that the process of$ e^+e^- \to Zh $ has been studied in Ref. [12], here we just include the corresponding result for comparison.The remainder of the paper is organized as follows. In Sec. II, we briefly introduce the SDFDM model and calculate its one-loop effects on five SM processes (
$e^+e^- \rightarrow \mu^+ \mu^-$ ,$ Zh, \; W^+W^-, \; ZZ $ , and$ Z \gamma $ ) at the CEPC. The combined 95% confidence results at the CEPC are also shown. In Sec. III, we show the results of the DTFDM model. Conclusions and discussions are provided in Sec. IV. -
In the SDFDM model [9–13], the dark sector contains one singlet Weyl spinor S and two doublet Weyl spinors
$ D_i $ ($ i=1,2 $ ) obeying the following$S U(2)_L \times U(1)_Y$ gauge transformations:$ \begin{aligned}[b] & S\in( {1}, 0) ,\; \; \; \; \; \; D_1=\left( \begin{array}{l} D^0_1 \\ D^-_1 \end{array} \right)\in( {2}, -1) ,\; \; \; \; \; \; \\& D_2=\left( \begin{array}{l} D^+_2 \\ D^0_2 \end{array} \right) \in( {2}, 1). \end{aligned} $

(1) The hypercharge signs of
$ D_1 $ and$ D_2 $ are opposite, which guarantees that the SDFDM model is anomaly free. The gauge invariant Lagrangians are given by$ \begin{aligned}[b] {\cal{L}}_S = & {\rm i} S^+ \bar{\sigma^{\mu}}D_{\mu}S - \frac{1}{2}(m_s S^T(-\epsilon)S + {\rm h.c.}) , \\ {\cal{L}}_D =& {\rm i} D_1^+ \bar{\sigma^{\mu}}D_{\mu}D_1 +{\rm i} D_2^+ \bar{\sigma^{\mu}}D_{\mu}D_2 \\&+ (m_D D^{iT}_1 (-\epsilon)D^j_2 + {\rm h.c.}) , \\ {\cal{L}}_Y =& y_1 S D_1^i H_i - y_2 S D_2^i \tilde{H_i} + {\rm h.c.}, \end{aligned} $

(2) where
$D_\mu=\partial_\mu -{\rm i} g t^j A^j_\mu -{\rm i} \dfrac{g'}{2}YB_\mu$ is the covariant derivative,$ t^j $ are the generators of the corresponding representation of$S U(2)_L$ , Y is the hypercharge,$\epsilon \equiv {\rm i}\sigma^2$ ,$ m_S $ and$ m_D $ are the mass parameters of the singlet and doublets, respectively, and$ y_1 $ and$ y_2 $ are two Yukawa couplings between the dark sector particles and Higgs boson. Consequently, this model has four independent parameters:$ m_S $ ,$ m_D $ ,$ y_1 $ , and$ y_2 $ .After EWSB, the Higgs field acquires the vacuum expectation value v and can be expressed in the unitary gauge as
$ \begin{array}{*{20}{l}} H=\dfrac{1}{\sqrt{2}} \left( \begin{array}{c} 0 \\ v+h \end{array} \right),\; \; \; \; \; \; \; \; \; \; \tilde{H}=\dfrac{1}{\sqrt{2}} \left( \begin{array}{c} v+h \\ 0 \end{array} \right). \end{array} $

(3) Subsequently, the Yukawa couplings result in mixing between the singlet Weyl spinor and doublet Weyl spinors. The mass terms of the dark sector particles are given by
$ \begin{aligned}[b] {\cal{L}}_m & = -\frac{1}{2}(S, D_1^0, D_2^0)M_n (-\epsilon) \left( \begin{array}{c} S \\ D_1^0 \\ D_2^0 \end{array} \right) - M_D D_1^- (-\epsilon)D_2^+ + {\rm h.c.} = -\frac{1}{2} m_{\chi^0_i} \sum \chi_i^0 (-\epsilon) \chi_i^0 - m_{\chi^{\pm}} \chi^- (-\epsilon) \chi^+ + {\rm h.c.} , \end{aligned} $ 
(4) where
$ \begin{array}{*{20}{l}} M_n = \begin{pmatrix} M_S & \dfrac{1}{\sqrt{2}} y_1 v & \dfrac{1}{\sqrt{2}} y_2 v \\ \dfrac{1}{\sqrt{2}} y_1 v & 0 & -M_D \\ \dfrac{1}{\sqrt{2}} y_2 v & -M_D & 0 \\ \end{pmatrix} \end{array} $

(5) is the mass matrix of the neutral particles,
$ \chi^0_i \; (i = 1,\; 2,\; 3) $ and$ \chi^\pm $ are the mass eigenstates,$ m_{\chi^0_i} $ and$ m_{\chi^\pm} $ are the masses of the corresponding mass eignestates. The mass eigenstates of the neutral particles$ \chi_i^0 $ are connected to the gauge eigenstates through the mixing matrix$ {\cal{N}} $ . That is,$ \begin{array}{*{20}{l}} {\cal{N}}^T M_n {\cal{N}} = {{\rm{diag}}}(m_{\chi^0_1},m_{\chi^0_2},m_{\chi^0_3}), \; \; \; \begin{pmatrix} S \\ D_1^0 \\ D_2^0 \\ \end{pmatrix} = {\cal{N}} \begin{pmatrix} \chi_1^0 \\ \chi_2^0 \\ \chi_3^0 \\ \end{pmatrix}. \end{array} $

(6) For convenience, we adopt the mass orders
$ m_{\chi^0_1} \leq m_{\chi^0_2} \leq m_{\chi^0_3} $ , which can be realized by adjusting$ {\cal{N}} $ . Because of the discrete$ Z_2 $ symmetry, the lightest neutral fermion$ \chi^0_1 $ is stable and can be considered a DM candidate. Moreover, we can construct four-component Dirac spinors from two-component Weyl spinors:$ \begin{array}{*{20}{l}} \Psi _i = \begin{pmatrix} \chi_i^0 \\ \epsilon (\chi_i^0)^{\dagger T} \\ \end{pmatrix}, \;\;\; \Psi^+ = \begin{pmatrix} \chi^+ \\ \epsilon (\chi^-)^{\dagger T} \end{pmatrix}. \end{array} $

(7) Thus, the mass terms and interaction terms of the SDFDM model can be rewritten as
$ \begin{aligned}[b] {\cal{L}}_{{\rm{SDFDM}}} =& -\frac{1}{2} m_{\chi^0_i} \overline{ \Psi_i} \Psi_i - m_{\chi^\pm} \overline{\Psi^+}\Psi^+ \\ & + -\frac{1}{\sqrt{2}} (y_1 {\cal{N}}_{1i} {\cal{N}}_{2j} + y_2 {\cal{N}}_{1i} {\cal{N}}_{3j}) h \overline{ \Psi_i} \Psi_j \\& + e A_\mu \overline{\Psi^+}\gamma^\mu \Psi^+ + (g\cos\theta - \frac{g\sin^2\theta}{\cos\theta})Z_\mu \overline{\Psi^+}\gamma^\mu \Psi^+ \\ & + \frac{g}{4\cos\theta} ( {\cal{N}}_{2i}^* {\cal{N}}_{2j} - {\cal{N}}_{3i}^* {\cal{N}}_{3j} ) Z_\mu \overline{\Psi_i^0}\gamma^\mu P_L\Psi_j^0 \\& - \frac{g}{4\cos\theta} ( {\cal{N}}_{2i}^* {\cal{N}}_{2j} - {\cal{N}}_{3i}^* {\cal{N}}_{3j} ) Z_\mu \overline{\Psi_j^0}\gamma^\mu P_R\Psi_i^0 \\ & - \frac{g}{\sqrt{2}} {\cal{N}}_{2i} W^- \overline{\Psi_i^0}\gamma^\mu P_R \Psi^+ + \frac{g}{\sqrt{2}} {\cal{N}}_{3i}^* W^- \overline{\Psi_i^0}\gamma^\mu P_L \Psi^+ \\& - \frac{g}{\sqrt{2}} {\cal{N}}_{2i}^* W^+ \overline{\Psi^+}\gamma^\mu P_R \Psi_i^0 + \frac{g}{\sqrt{2}} {\cal{N}}_{3i} W^+ \overline{\Psi^+}\gamma^\mu P_L \Psi_i^0. \end{aligned} $

(8) -
Although the dark sector particle
$ \chi = \{\chi^0_i,\; \chi^\pm\} $ cannot be directly produced at the collider when$ 2m_{\chi}>\sqrt{s} $ , it can still affect the cross sections of the SM processes through loop effects, which means that the hint of dark sector particles may be revealed through precision measurements. In this paper, we focus on five processes,$ e^+ e^- \rightarrow \mu^+\mu^-, \; Zh, \; W^+W^-, \; ZZ, $ and$ Z\gamma $ at the CEPC, and calculate the deviation of the cross section induced by the dark sector particles from the SM prediction at the one-loop level. The corresponding Feynman diagrams of one-loop contributions are given in Appendix A. By utilizing the high precision of the CEPC, these deviations can consequently provide effective constraints on the parameter space of the new physical model. In our calculations, the Packages FeynArts 3.10 [30], FormCalc 9.7 [31], and LoopTools 2.15 [31] are used to generate Feynman diagrams and derive the numerical results. Note that the entire calculation is performed under the on-shell renormalization scheme.The cross section at the next to leading order with the EW correction can be expressed as
$ \begin{array}{*{20}{l}} \sigma = \sigma_{{{\rm{LO}}}}+\sigma_{{\rm{NLO}}}^{{\rm{EW}}}+\sigma_{{\rm{NLO}}}^{{\rm{Soft}}}, \end{array} $

(9) where
$ \sigma_{{{\rm{LO}}}} $ is the tree-level cross section,$ \sigma_{{\rm{NLO}}}^{{\rm{EW}}} $ is the EW correction at the one-loop level.$ \sigma_{{\rm{NLO}}}^{{\rm{Soft}}} $ is the contribution from the soft bremsstrahlung diagrams, which cancels the infrared divergences originating from the diagrams with the exchange of virtual photons. The deviation of the cross-section from the SM prediction can be expressed as$ \frac{\Delta\sigma}{\sigma_0} = \frac{\mid \sigma_{{{\rm{SDFDM}}}}-\sigma_{{{\rm{SM}}}} \mid}{\sigma_{{{\rm{SM}}}}}, $

(10) where
$ \sigma_{{{\rm{SDFDM}}}} $ and$ \sigma_{{{\rm{SM}}}} $ are the one-loop cross sections of the SDFDM model and SM, respectively (see (9)). For the five processes considered here, the leading contributions to$ \Delta \sigma $ result from the interferences between the SM amplitudes at the leading order and the amplitudes involving the particles in the dark sector.Note that for the process
$ e^+ e^- \to Z \gamma $ , the cross section contains collinear divergence even at the tree-level. However, considering that the collinear photons cannot be detected owing to the blind spot of the detector, the collinear divergence can be removed by excluding the collinear photons. Here, we calculate the cross section with$ |\cos\theta_{\gamma}|<0.99 $ , where$ \theta_{\gamma} $ is the angle between the photon and beam.The precision of the CEPC is determined by the statistical and systematic uncertainties. In this analysis, we treat these uncertainties as independent numbers. The statistical uncertainty can be estimated from the predicted event numbers N, that is,
$ \sim 1/\sqrt{N} $ , whereas the systematic uncertainties are primarily from the uncertainty of integrated luminosity and the misidentification of final states. Thereinto, the integrated luminosity uncertainty at the CEPC is$ \sim 0.1\% $ [5]. For the process of$ e^+ e^- \to \mu^+ \mu^- $ , the misidentification uncertainty can be ignored owing to the excellent capability of the muon reconstruction. Note that the leptonic and semileptonic decays of the gauge bosons can also be well reconstructed, whereas distinguishing the two jets from one gauge boson in the pure hadronic decay is difficult. For simplicity, in our analysis, we consider only the cross sections from leptonic and semileptonic decays; thus, the reconstruction of the gauge bosons would have a high efficiency. In this case, we assume that the systematic uncertainties of$ e^+ e^- \to W^+W^-,\; ZZ $ , and$ Z\gamma $ are only from integrated luminosity②.According to the number of events in Sec. I, the statistical uncertainties of
$ e^+ e^- \to \mu^+ \mu^- $ ,$ W^+W^- $ ,$ ZZ $ , and$ Z\gamma $ are estimated as 0.032%,$ 0.014\% $ ,$ 0.059\% $ , and$ 0.014\% $ , respectively. Combined with the systematic uncertainties, the corresponding precision of these processes are about$ 0.1\% $ ,$ 0.1\% $ ,$ 0.12\% $ , and$ 0.1\% $ . The precision of$ e^+ e^- \to Zh $ is given as 0.5% by Ref. [5]. -
In this section, we study the capability of the CEPC to probe the parameter space of the SDFDM model. Considering that the SDFDM model has four free parameters, i.e.,
$ y_1,\; y_2,\; m_S, $ and$ m_D $ , we propose to show the calculation results of$ \Delta \sigma/\sigma_{{\rm{SM}}} $ on the Yukawa plane ($ y_1-y_2 $ ) or/and mass plane ($ m_S-m_D $ ). Here, we select three sets of benchmark parameters: (1)$ y_1 = 1.0 $ and$ y_2 = 0.5 $ ; (2)$ M_S = 100 $ GeV and$ M_D = 400 $ GeV; (3)$ M_S = 400 $ GeV and$ M_D = 200 $ GeV. Considering that the Yukawa interaction induced mass mixing between the singlet and doublets (see Eq. (2)) are at the order of the EWSB scale$ \sim {\cal{O}} $ (100) GeV, the benchmark parameters (2) and (3) represent the DM candidate$ \chi^0_1 $ that is roughly singlet-dominated and doublet-dominated, respectively. The corresponding results are shown in Fig. 1, Fig. 3, and Fig. 4.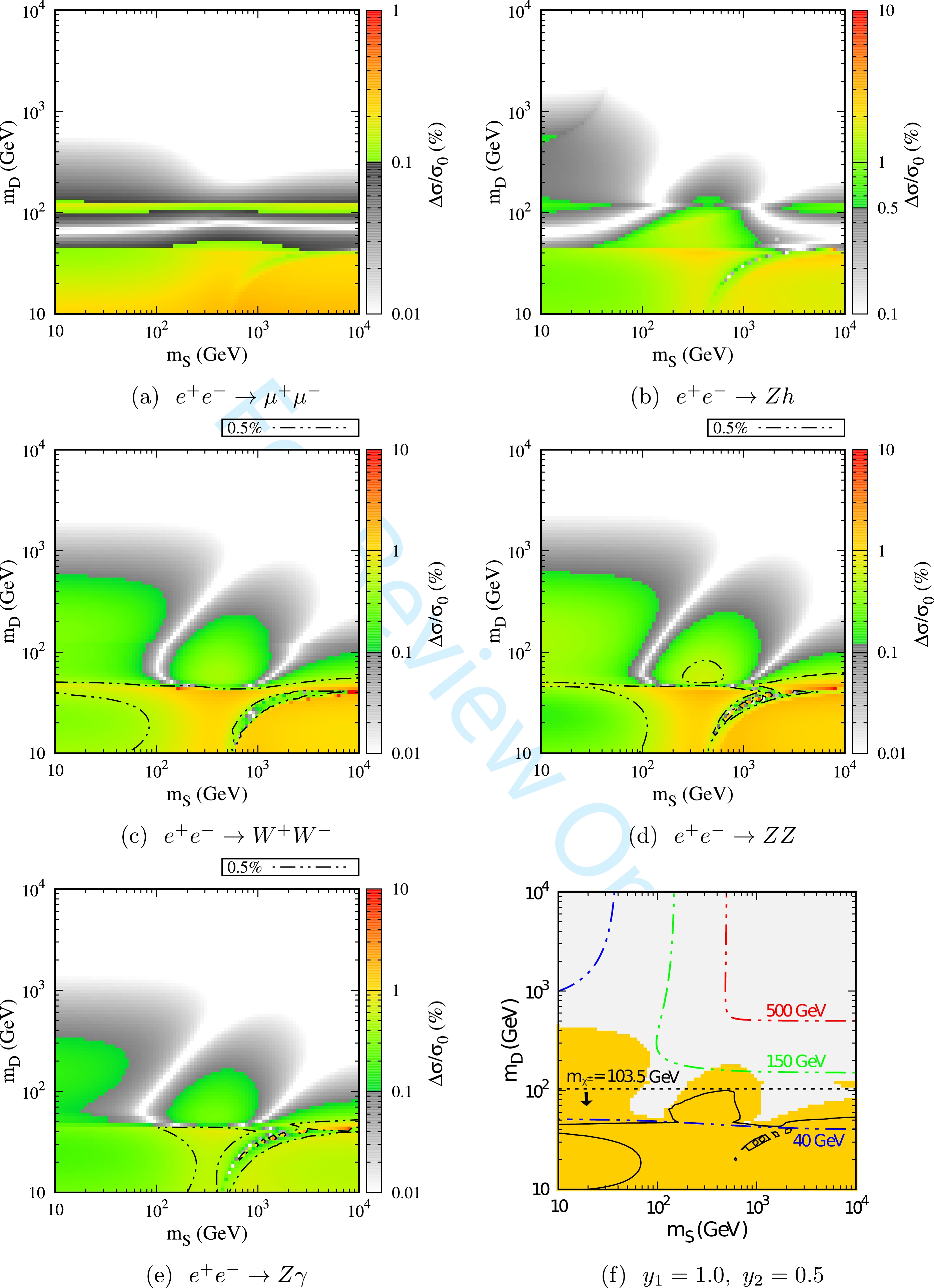
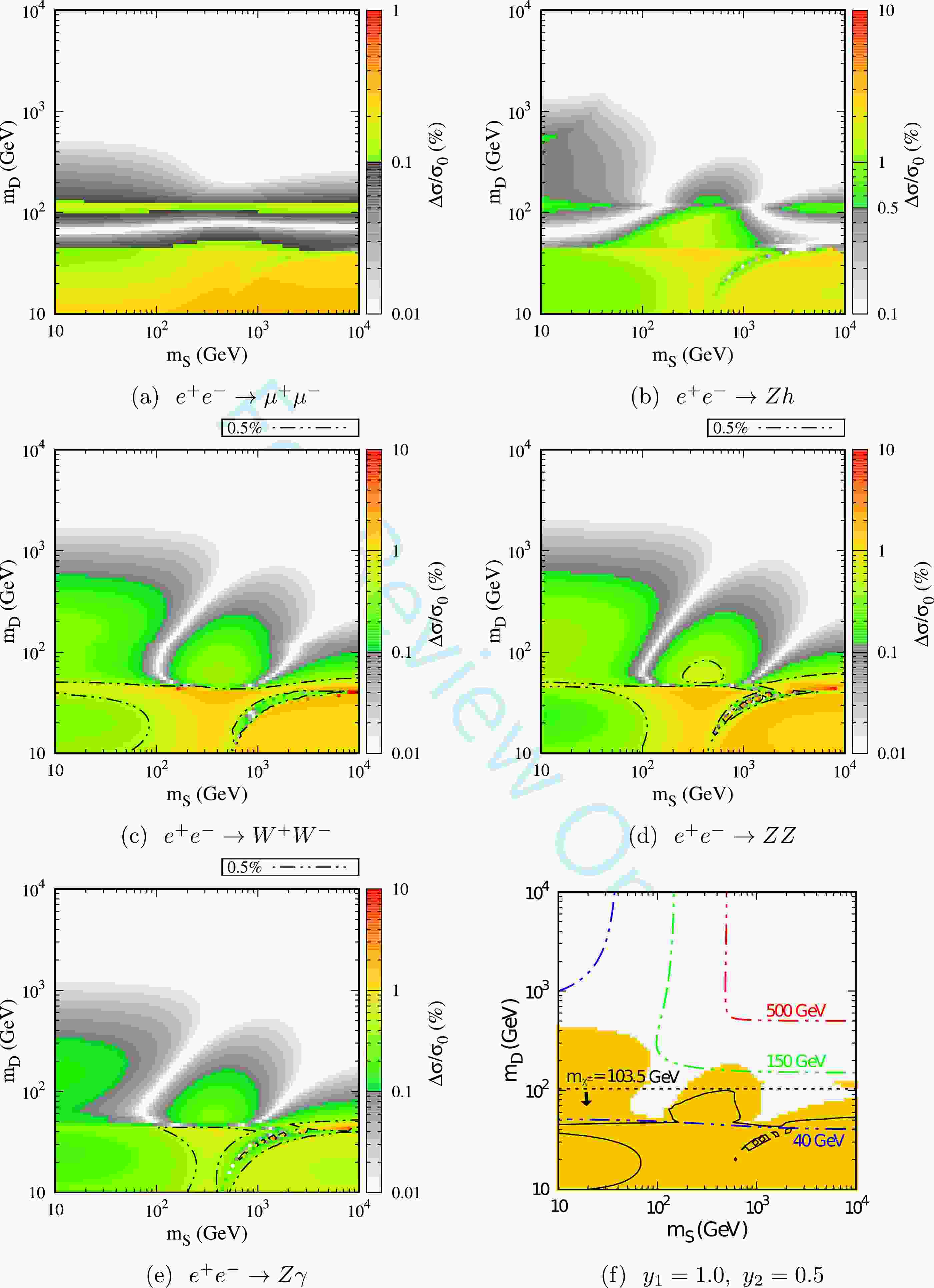
Figure 1. (color online) Heat maps for the relative deviation of
$ e^+e^- \to \mu^+\mu^-,\; Zh,\; W^+W^-, \; ZZ $ , and$ Z\gamma $ are shown in (a)$ \sim $ (e). The colored regions indicate that$ \Delta \sigma/\sigma_0 $ is larger than the expected sensitivities of the CEPC. The dot dashed lines in (c) (d) (e) correspond to a conservative estimate with$ \Delta \sigma/\sigma_0 = 0.5 $ %. The combined result of all these channels at the 95% confidence level is shown in (f), where the dot dashed line represents the mass contour of$ \chi^0_1 $ . The regions below the dotted black line are excluded by the search for charged particles at the LEP [32]. The solid black lines indicate constraints from conservative estimation. All these results are derived with fixed Yukawa couplings of$ y_1 = 1.0 $ and$ y_2 = 0.5 $ .
Figure 3. (color online) Same as Fig. 1, but in the
$ y_1-y_2 $ plane with the fixed mass parameters of$ M_S = 100 $ GeV and$ M_D = 400 $ GeV.
Figure 4. (color online) Same as Fig. 1, but in the
$ y_1-y_2 $ plane with the fixed mass parameters of$ M_S = 400 $ GeV and$ M_D = 200 $ GeV.In Fig. 1, we show the results of first set of benchmark parameters, where Fig. 1(a)
$ \sim $ Fig. 1(e) represent the processes$ e^+e^- \to \mu^+ \mu^- $ ,$ Zh $ ,$ W^+W^- $ ,$ ZZ $ , and$ Z \gamma $ , respectively. Fig. 1(f) represents the combined result of all these channels at the 95% confidence level (see details below). The colored parameter regions indicate that$ \Delta \sigma/\sigma_0 $ is larger than the precision of the CEPC and can thus be explored in a future measurement. For a conservative estimate, we also consider a precision of$ 0.5\% $ for the processes of$ e^+e^-\to W^+W^- $ ,$ ZZ $ , and$ Z \gamma $ , and show the corresponding results in Fig. 1, Fig. 3, and Fig. 4.In comparison with other channels, the result of
$ e^+ e^- \to \mu^+ \mu^- $ (see Fig. 1(a)) is relatively simpler. We observe that the colored regions are strongly dependent on$ m_D $ and almost independent of$ m_S $ . Considering that the dark sector particles in the SDFDM model do not interact with leptons, the deviation of this process is dominantly induced by the corrections to the propagators, i.e., Z and/or γ, as shown in Appendix A. For the charged particle$ \chi^\pm $ (pure doublet), its coupling to Z and γ is constant (see Eq. (8)); thus, the corrections induced by$ \chi^\pm $ only depend on$ m_D $ . For the neutral particles$ \chi^0_i $ , the results are similar for$ m_D \ll m_S $ , because in this case, the lighter neutral particles$ \chi^0_1 $ and$ \chi^0_2 $ are also doublet dominated. Our calculation shows that the contribution of the SDFDM model to$ e^+e^- \to \mu^+ \mu^- $ is dominated by doublets, which is consistent with Fig. 1(a). Moreover, the corrections from the NP particles in the loop would change dramatically when some mass conditions are fulfilled. These mass threshold effects might partially explain the structures in Fig. 1.In Fig. 2, we show some typical mass conditions with
$ y_1 = 1.0 $ and$ y_2 = 0.5 $ , e.g.,$ m_{\chi^0_1}+m_{\chi^0_1}(m_{\chi^0_2})=\sqrt{s} $ ,$2m_{\chi^-}= \sqrt{s}$ ,$ m_{\chi^0_1}+m_{\chi^0_1}(m_{\chi^0_2})=m_Z $ ,$ 2m_{\chi^-}=m_Z $ , and$m_{\chi^0_i}+m_{\chi^-}= m_{W^-}$ . For$ e^+e^- \to \mu^+ \mu^- $ , we observe that the NP correction reaches a maximum value at$ m_D \sim 45 $ GeV with$ 2m_{\chi_1^0}\sim m_Z $ and$ 2m_{\chi_-}\sim m_Z $ , and then with the increase in$ m_D $ , the NP correction rapidly decreases to zero and changes to an opposite sign until the next mass threshold appears. This behavior could explain the gray band of Fig. 1(a) within 50 GeV$ \lesssim m_D \lesssim 80 \; {{\rm{GeV}}} $ , where the correction of NP is too small to detect. When the next threshold appears at$ m_D \sim 120 $ GeV with$ 2m_{\chi^-}=\sqrt{s} $ , the NP correction reaches a minimum value and thus$ \Delta \sigma/\sigma_0 $ reaches a new maximum value. When$ m_D \gtrsim 120 $ GeV, the absolute value of the correction is suppressed by the large masses of the NP particles in loops. Another striking feature is that the results of$ e^+ e^- \to W^+W^- $ ,$ ZZ $ , and$ Z\gamma $ are similar (see Fig. 1(c)$ \sim $ Fig. 1(e)). We observe that the contributions from the triangle loops connecting to three gauge bosons for these processes are actually sub-dominant. The main NP corrections are provided by the t-channel diagrams with the insertion of the counter terms, which involve the contributions of the NP particles, into the vertex between the gauge boson and leptons. The related Feynman diagrams are provided in Appendix A.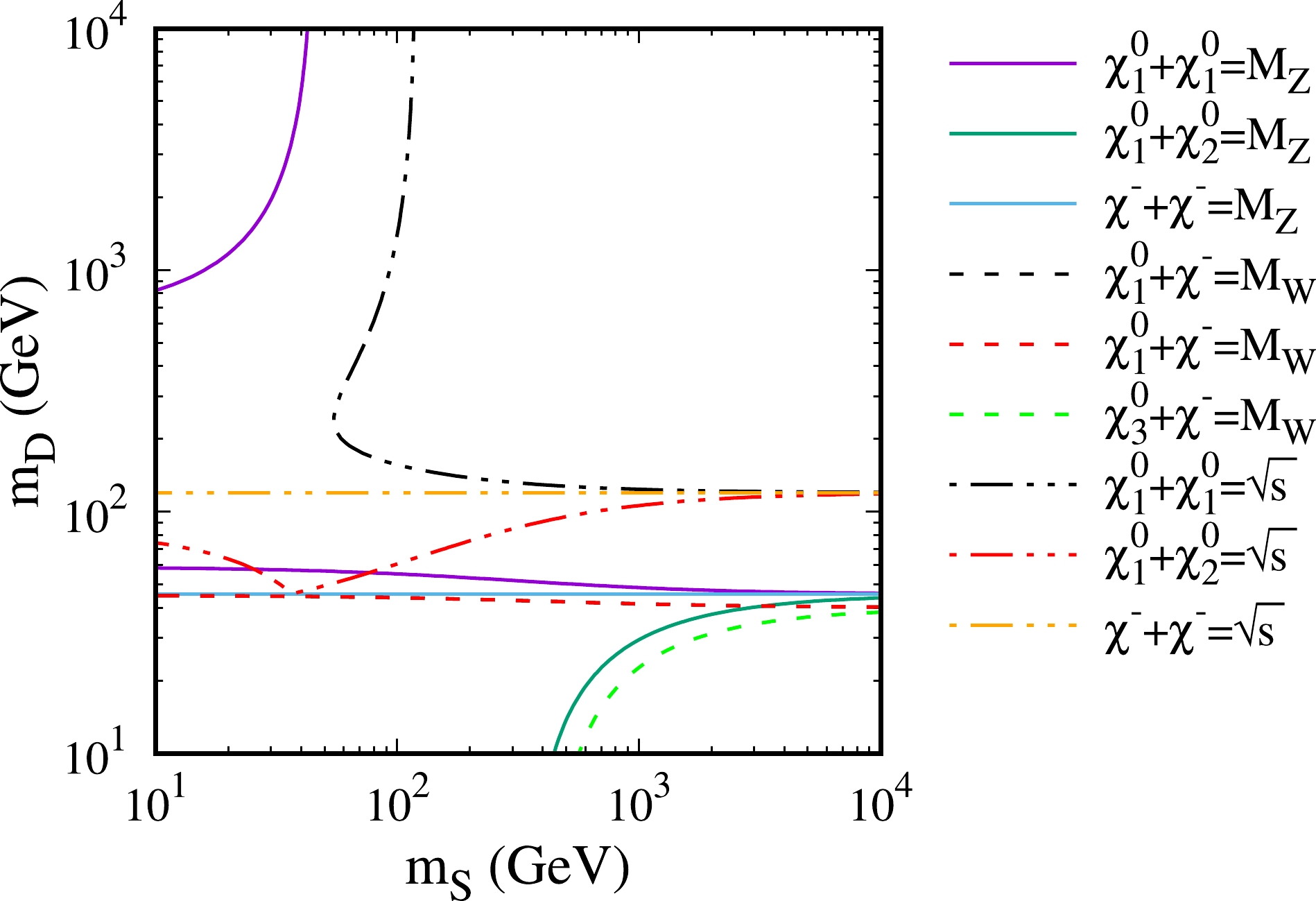
Figure 2. (color online) Contours for the mass threshold conditions with
$ y_1 = 1.0 $ and$ y_2 = 0.5 $ .For the second benchmark case, i.e.,
$ m_S = 100\; {\rm{GeV}} $ and$ m_D = 400\; {\rm{GeV}} $ , the corresponding results are shown in Fig. 3. In this case, the$ \chi^0_1 $ is dominated by the singlet and is much lighter than the other NP particles. Therefore, for the process$ e^+ e^- \to \mu^+\mu^- $ , the NP correction significantly depends on the$ Z\chi^0_1\chi^0_1 $ coupling. We observe that$ |y_1| = |y_2| $ results in a vanishing$ Z\chi^0_1\chi^0_1 $ coupling; thus, the NP correction induced by$ \chi^0_1 $ is highly suppressed, which rends a non-detectable parameter region around$ |y_1| \approx |y_2| $ at the CEPC (see Fig. 3(a)). The structures for the processes of$ e^+ e^- \to W^+W^- $ ,$ ZZ $ , and$ Z\gamma $ are also similar. However, the parameter regions with$ \mid y_1 \mid \approx \mid y_2 \mid \gtrsim 1 $ can be detected at the CEPC, which is different from the process$ e^+ e^- \to \mu^+\mu^- $ .For the third benchmark case, i.e.,
$ m_S = 400\; {\rm{GeV}} $ and$ m_D = 200\; {\rm{GeV}} $ , the results are shown in Fig. 4. Both the neutral particles$ \chi_1 $ and$ \chi_2 $ are doublet-dominated, whereas$ \chi_3 $ is singlet-dominated. In this case,$ \chi^0_1 $ and$ \chi^0_2 $ would provide a comparable contribution to the deviation. However, comparing this with the second benchmark case, the masses of$ m_{\chi^0_1} $ and$ m_{\chi^0_2} $ are heavier, which rends a relatively smaller detectable parameter regions.From the results shown in subfigures (a)
$ \sim $ (e) of Fig. 1, Fig. 3, and Fig. 4, we observe that for different channels, the parameter space that can be explored by the CEPC are actually complementary. Therefore, we propose to combine all these five processes and perform a likelihood analysis to obtain a more efficient constraint on the parameter space [23, 27]. We define a$ \chi^2 $ function as$ \chi^2 = \sum\limits_i \frac{(\mu_i^{\rm NP} - \mu_i^{\rm obs})^2}{\sigma^2_{\mu_i}}\simeq \sum\limits_i \frac{(\Delta \sigma/\sigma_0)^2}{\sigma^2_{\mu_i}}, $

(11) where
$\mu_i^{\rm NP} = \sigma^{\rm NP}_i/\sigma^{\rm SM}_i$ is the ratio of the NLO cross section between NP and the SM,$\mu_i^{\rm obs}$ is assumed to be 1, and$ \sigma_{\mu_i} $ is the estimated CEPC precision for the i-th process (see Sec. II.B). For a two-parameter fitting, the corresponding$ \delta \chi^2=\chi^2-\chi_{{{\rm{min}}}}^2 $ at the 95% confidence level is 5.99. The corresponding combined results are shown in Fig. 1(f), Fig. 3(f), and Fig. 4(f), respectively. For instance, when$ y_1 $ = 1.0 and$ y_2 $ = 0.5, the precision measurements at the CEPC could explore the mass of$ \chi^0_1 $ nearly up to$ m_{\chi_1^0} \sim 150\; {\rm{GeV}} $ at the 95% confidence level.For the lightest chargino search in supersymmetric models at the LEP, the mass of new charged particles less than 103.5 GeV has been almost excluded [32]. We impose this limit on
$ m_{\chi^{\pm}} $ in the SDFDM model here and show the corresponding results in Fig. 1(f). Ref. [12] observed that at the LHC, the monojet+$\not E_{\rm{T}}$ channel could set more strict constraints than other channels, such as$2\ell + \not E_{\rm{T}}$ and$3\ell + \not E_{\rm{T}}$ . Such constraints on$ m_{\chi^0_1} $ are not stronger than$ \sim 100 $ GeV. The detectability of the CEPC would be complementary to the LEP and LHC in some parameter regions.Ref. [12] also observed that the constraints from the DM relic abundance and direct detection are generally more stringent in a large portion of the parameter space. In this paper, we do not repeat all the analyses from other experiments and only demonstrate the constraints from the DM relic abundance and direct detection in Appendix B. We observe that the DM direct detection experiments have set very stringent constraints on the parameter space. However, some allowed parameter regions with
$ y_1\sim y_2 $ can still be tested by the CEPC. -
In the DTFDM model [11–14], the dark sector contains one triplet Weyl spinor T and two doublet Weyl spinors
$ D_i $ ($ i=1,2 $ ) obeying the following$S U(2)_L \times U(1)_Y$ gauge transformations:$ \begin{aligned}[b]& D_1=\left( \begin{array}{l} D^0_1 \\ D^-_1 \end{array} \right)\in( {2}, -1) ,\; \; \; \; \; \; D_2=\left( \begin{array}{l} D^+_2 \\ D^0_2 \end{array} \right) \in( {2}, 1) ,\\& T = \left( \begin{array}{l} T^+ \\ T^0 \\ -T^- \end{array} \right) \in( {3}, 0) . \end{aligned} $

(12) The gauge invariant Lagrangians of the dark sector particles are given by
$ \begin{aligned}[b] {\cal{L}}_T =& {\rm i} T^+ \bar{\sigma^{\mu}}D_{\mu}T + \frac{1}{2}(m_T T^T(-\epsilon)T + {\rm h.c.}), \\ {\cal{L}}_D =& {\rm i} D_1^+ \bar{\sigma^{\mu}}D_{\mu}D_1 + {\rm i} D_2^+ \bar{\sigma^{\mu}}D_{\mu}D_2 \\&+ (m_D D^{iT}_1 (-\epsilon)D^j_2 + {\rm h.c.}), \\ {\cal{L}}_Y =& y_1 T D_1^i H_i + y_2 T D_2^i \tilde{H_i} + {\rm h.c.}. \end{aligned} $

(13) Similarly, the model also has four free parameters, including two mass parameters,
$ m_T $ and$ m_D $ , and two Yukawa couplings,$ y_1 $ and$ y_2 $ . The EWSB results in the mixing between the triplet and two doublets. In the base of mass eigenstate, we obtain three neutral Majorana fermions$ \chi^0_i $ ($i = $ 1, 2, 3) and two charged Dirac fermions$ \chi_i^\pm $ ($i= $ 1, 2). The full Lagrangians expressed in the terms of four-component spinors can are provided in Ref. [12].Compared with the SDFDM model, the DTFDM model contains one more charged particle, which would induce a relatively larger
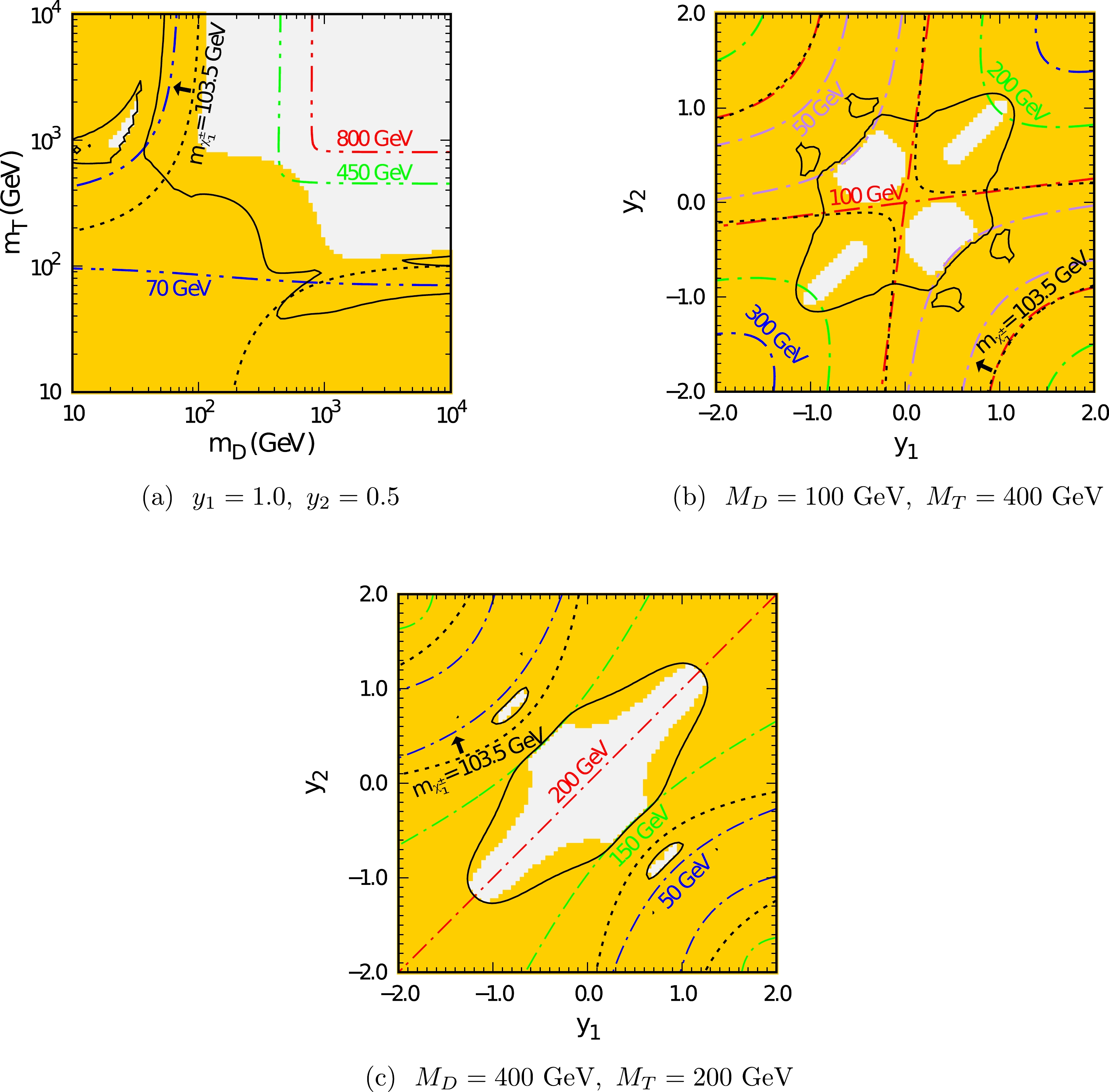
$ \Delta \sigma/\sigma_0 $ . In Fig. 5, we show the combined constraints from the five processes in the$ y_1-y_2 $ and$ m_D-m_T $ planes, where the yellow regions can be explored by the CEPC at the 95% confidence level.In Fig. 5(a), we observe that the parameter regions with small
$ m_D $ or$ m_T $ can be explored by the CEPC. Similar to the results of the SDFDM model for$ m_D \lesssim $ 100 GeV, the deviation induced by the DTFDM model can be probed, because two lighter neutral NP particles are doublet dominated and have small masses. However, unlike the results of the SDFDM model for$ m_D > 1 $ TeV and$ m_s \lesssim $ 100 GeV, the deviation induced by the DTFDM model for$ m_D > 1 $ TeV and$ m_T \lesssim $ 100 GeV can still be probed. This is because, in this parameter region, except for the lightest neutral NP particles, the lighter charged particles are dominated by the triplet components and have small masses. In Fig. 5(a) we also show the mass contour of$ \chi_1^0 $ as in Fig. 1, Fig. 3, and Fig. 4. We observe that the CEPC has the capability to indirectly detect$ m_{\chi^0_1} $ up to 450 GeV.For the fixed mass parameters
$ m_D = $ 100 GeV and$ m_T = $ 400 GeV, almost all the parameter regions with$ |y_1|<2 $ and$ |y_2|<2 $ can be excluded by the CEPC, as shown in Fig. 5(b). This is because$ \chi^0_1 $ ,$ \chi^0_2 $ , and$ \chi^\pm_1 $ are doublet dominated and provide significant contributions to the NP correction owing to small masses. The result for the fixed mass parameters$ m_D = $ 400 GeV and$ m_T = $ 200 GeV is shown in Fig. 5(c). In this case, the triplet dominated$ \chi^0_1 $ and$ \chi^\pm_1 $ have relatively large masses in the parameter region with$ y_1\approx y_2 $ , where the couplings$ Z\chi^0_i\chi^0_i $ are suppressed. Thus, a larger region cannot be detected by the CEPC compared with the previous case. Other constraints on the DTFDM model are simialr to those on the SDFDM model. We provide the constraints on the parameter space of the DTFDM model set by the DM relic density and the direct detection in Appendix B. -
In this paper, we study the effects of the EW multiplet fermionic dark matter models through precision measurements at the future electron-positron collider, the CEPC. As a Higgs factory, the CEPC will significantly increase the accuracy of the EW measurements owing to its relatively clean environment and large luminosity
$ \sim5.6 $ ab$ ^{-1} $ . In particular, the sensitivity of$ e^+e^- \to \mu^+\mu^-, \; Zh, \; W^+W^-, \; ZZ $ , and$ Z\gamma $ can even reach a sub-percentage level. Thus, any possible deviations from the SM prediction can be considered a hint of NP.We focus on two fermionic dark matter models, namely the SDFDM and DTFDM models. In these models, two types of fermionic multiplets under the
$S U(2)_L$ representation are introduced based on the SM. We calculate the one-loop deviations induced by the NP particles for the abovementioned five SM processes and investigate the parameter regions that can be detected by the CEPC. Considering that the results of these channels are complementary for both models, we adopt a combined analysis and obtain a more efficient constraint on the model parameter space. For$ y_1 $ = 1.0 and$ y_2 $ = 0.5, we observe that the CEPC can probe$ m_{\chi^0_1} $ up to$ \sim 150\; {\rm{GeV}} $ and$ \sim 450 $ GeV at the 95% confidence level for the SDFDM and DTFDM models, respectively. -
The authors would like to thank Manqi Ruan for helpful discussions.
-
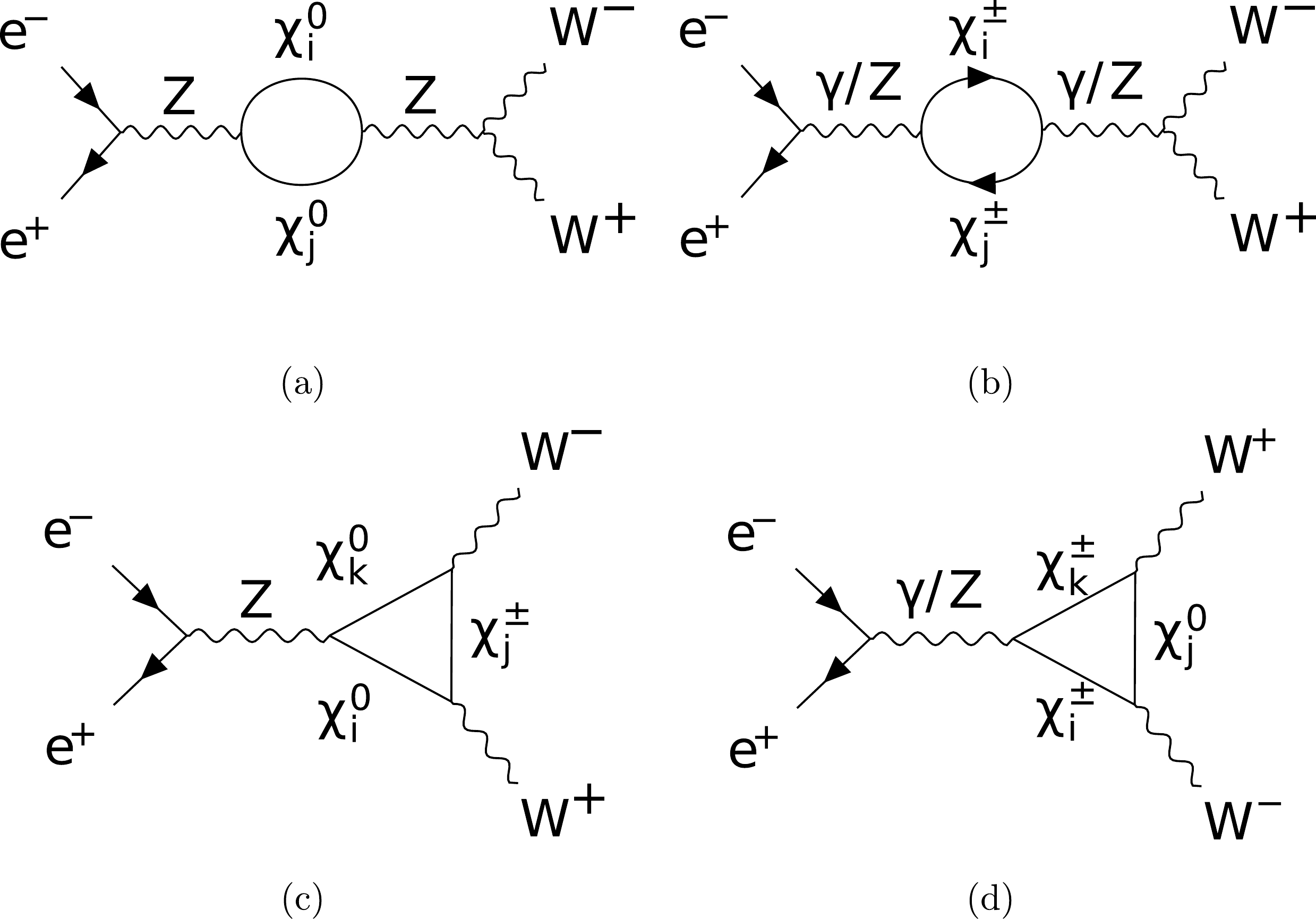
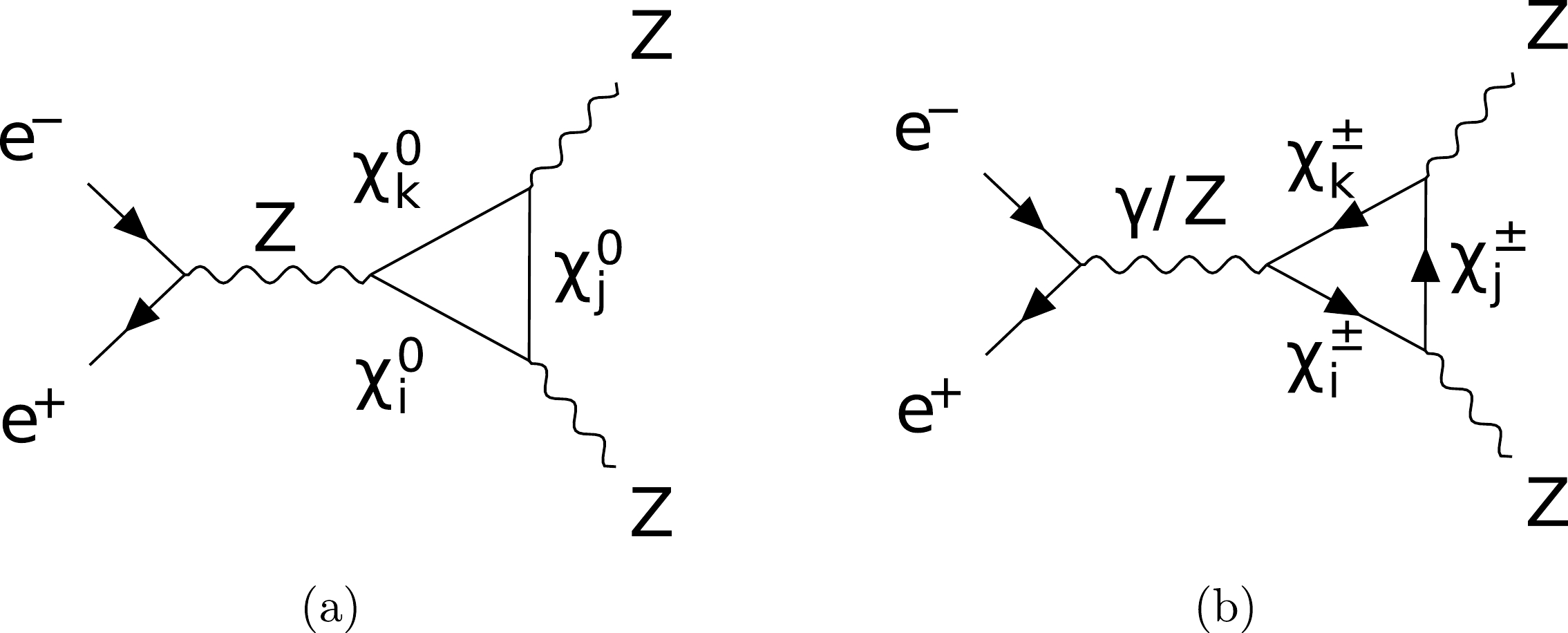
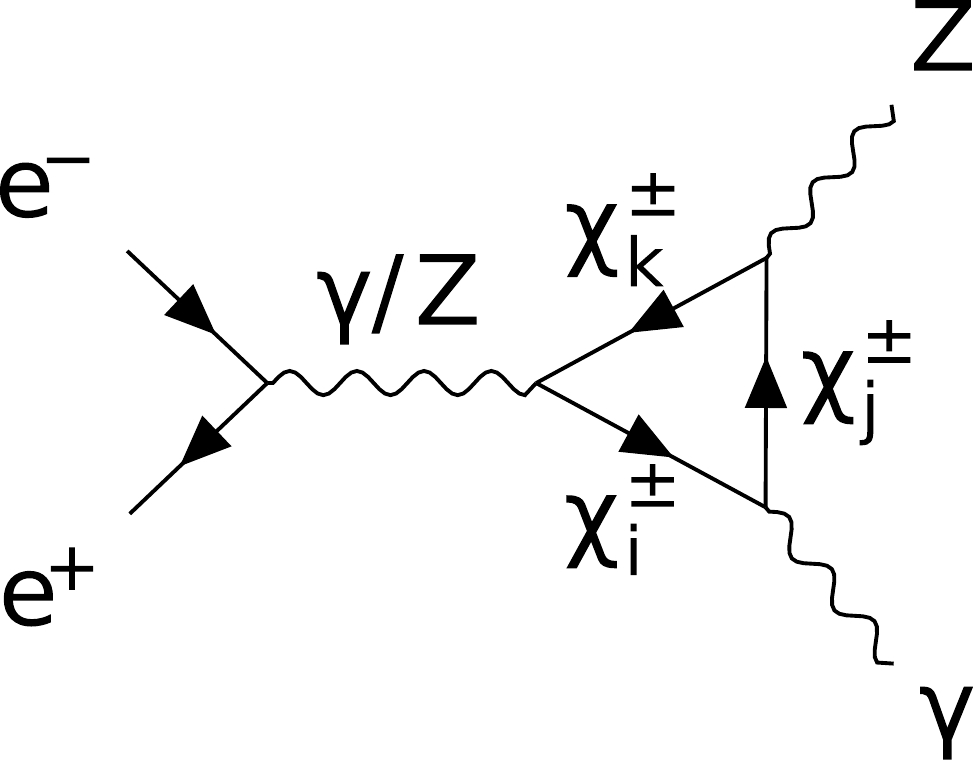
Feynman diagrams contributed by the new particles in the loop for the SDFDM and DTFDM models are provided here. For the SDFDM model, the new particles contain
$ \chi^0_i $ (i=1,2,3) and$ \chi^{\pm}_j $ (j=1). For the DTFDM model, the new particles contain$ \chi^0_i $ (i=1,2,3) and$ \chi^{\pm}_j $ (j=1,2). Fig. A1, Fig. A2, Fig. A3, Fig. A4, and Fig. A5 correspond to the processes$ e^+e^- \to \mu^+\mu^-, \; Zh, \; W^+W^-, \; ZZ $ , and$ Z\gamma $ , respectively. For$ e^+e^- \to \; W^+W^- $ ,$ZZ $ , and$ Z\gamma $ , we also show the Feynman diagrams of the t-channel processes with the insertion of the counter terms into the vertex between the gauge boson and leptons. These diagrams with the counter terms involving the NP contributions provide leading corrections to the related cross sections.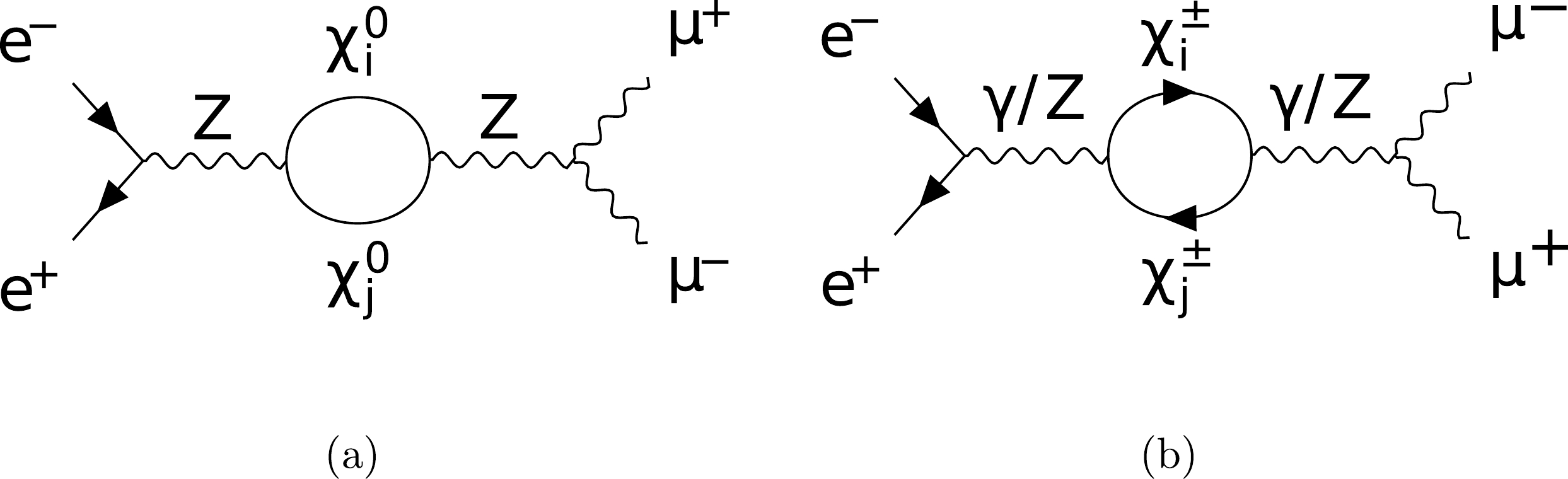
Figure A1. Feynman diagrams for the propagator (a, b) corrections to
$ e^+ e^- \to \mu^+ \mu^- $ due to the dark sector in both models.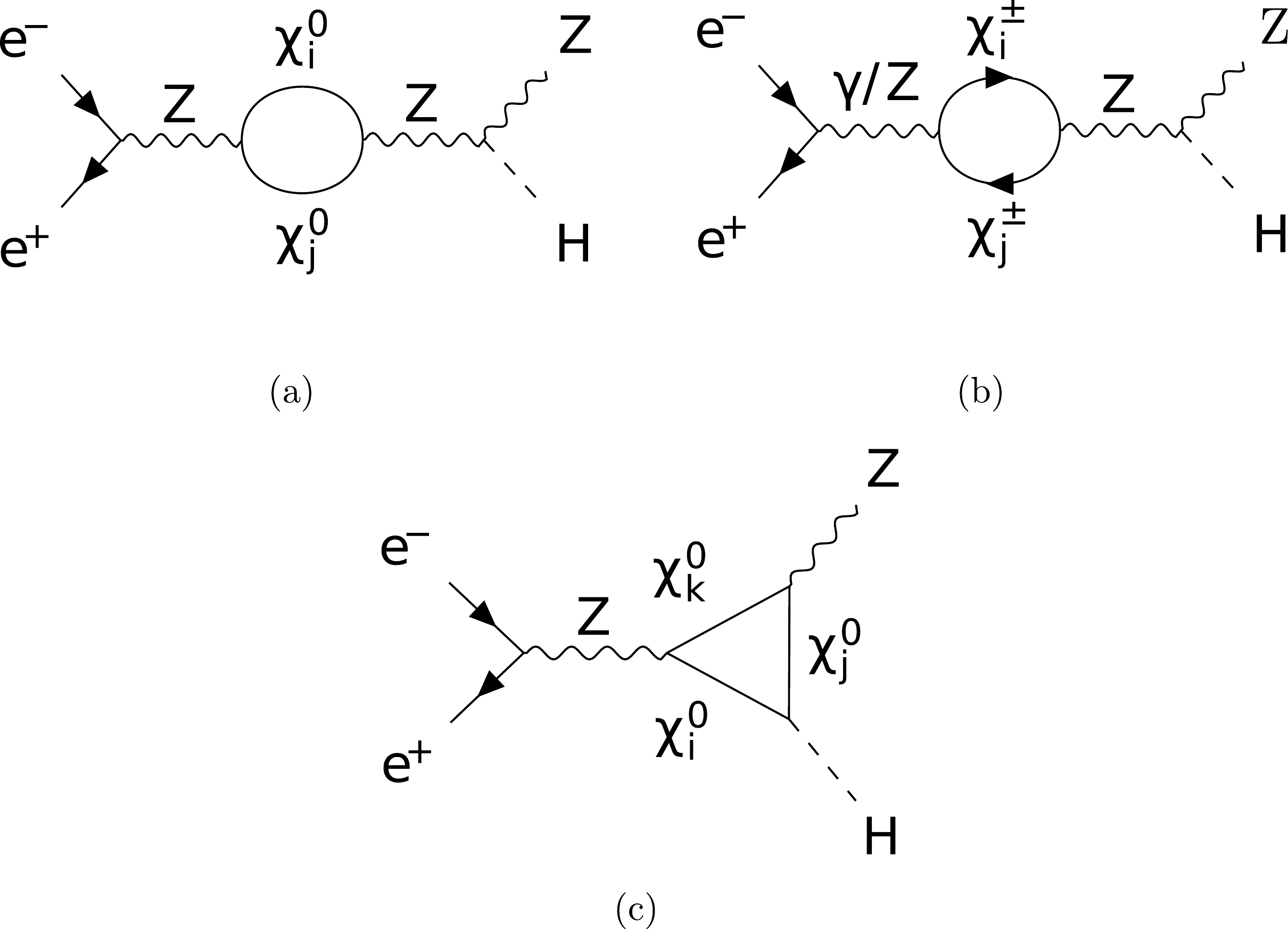
Figure A2. Feynman diagrams for the vertex (a) and propagator (b, c) corrections to
$ e^+ e^- \to Z H $ . -
In Fig. B1 and Fig. B2, we show the constraints from the DM relic abundance and direct detection for the SDFDM and DTFDM models, respectively. For the relic abundance, the effects of all the annihilation and coannihilation channels are calculated using the package MadDM [33]. The blue regions are excluded because of the predicted DM relic abundance is larger than the observed value with
$ \Omega h^2 > 0.12 $ [34]. For comparison, we have selected the same parameters in Fig. B1(a), B1(b), B1(c), B2(a), B2(b), and B2(c) as in Fig. 1(f), 3(f), 4(f), 5(a), 5(b), and 5(c). We also consider the constraints from the DM direct detection and show the excluded parameter regions in Fig. B1 and Fig. B2. The experimental limits on the spin-independent (SI) and spin-dependent (SD) DM-nucleon scatterings are obtained from the results of PandaX-4T [35] and PICO-60 [36], respectively. The DM-nucleon scattering cross sections are also calculated using MadDM.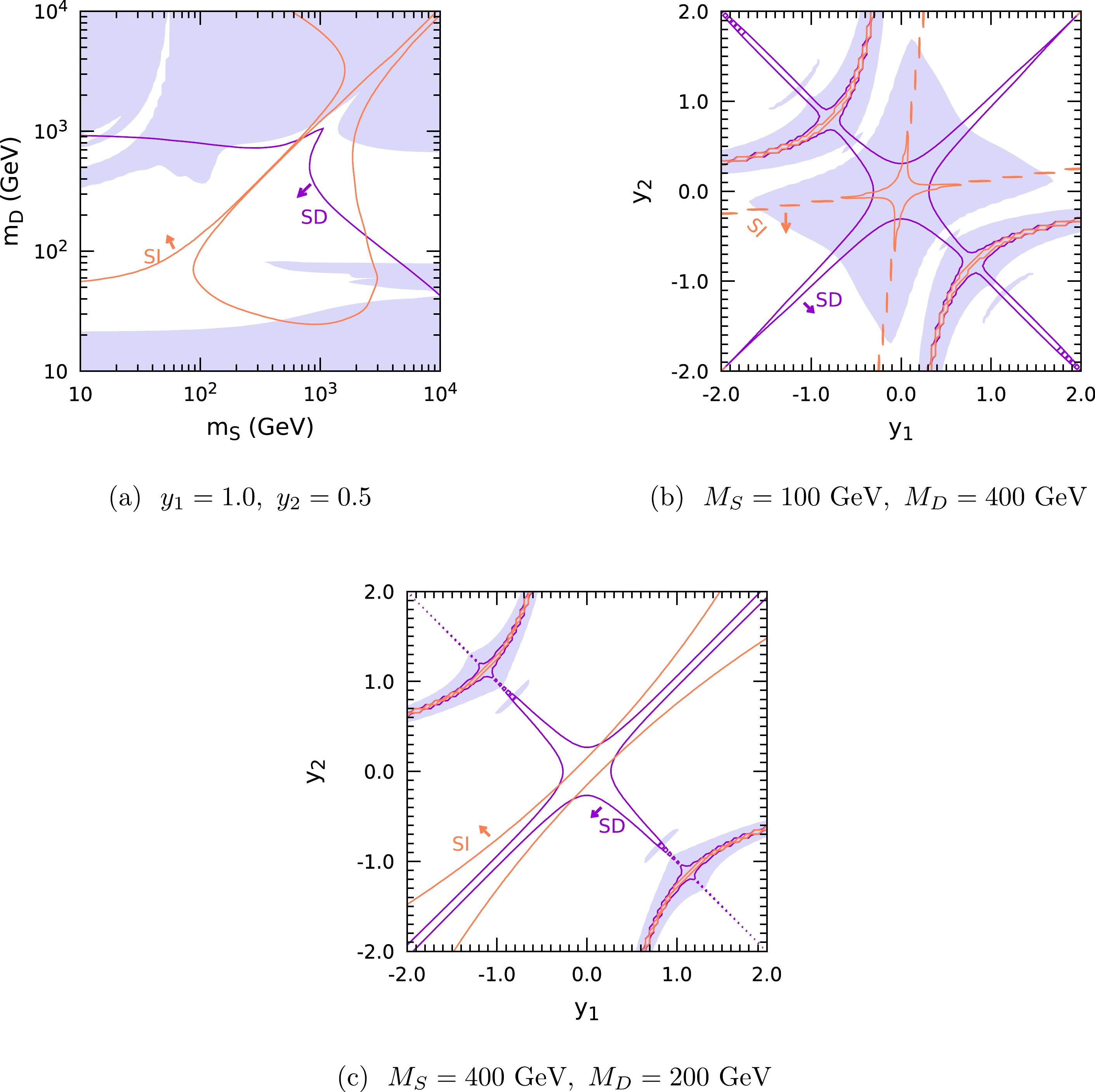
Figure B1. (color online) DM constraints in the
$ m_S-m_D $ (a) and$ y_1-y_2 $ (b, c) planes for the SDFDM model. The blue regions represent the parameter regions, where the predicted DM relic abundance is larger than the observed value [34] with$ \Omega h^2 > 0.12 $ . The orange and purple lines represent the constraints set by the direct detection PandaX-4T [35] for the SI scattering and PICO-60 [36] for the SD scattering, respectively. The arrows denote the directions for exclusion.
Figure B2. (color online) Same as Fig. B1, but for the DTFDM model.
The DM overproduction limit excludes the parameter regions in which the DM annihilation cross section is excessively small. For the SDFDM model,
$ m_D \gtrsim 1 $ TeV in Fig. B1(a) can be excluded by the DM overproduction limit. This is because when$ m_D $ is large, the DM annihilation cross section would be significantly suppressed owing to the small doublet components in the DM. In Fig. B1(b), although$ m_D $ is not very large, small$ m_S $ ,$ y_1 $ , and$ y_2 $ may also result in a DM dominated by the singlet component. Moreover, in Fig. B1(b) and B1(c), if$ y_1 $ and$ y_2 $ have opposite signs, a parameter region may occur in which the DM is very light owing to the large mass splitting term. These parameter regions are excluded by the overproduction limit because the DM particles do not have a significant annihilation cross section.The couplings of
$ h\chi_1^0\chi_1^0 $ and$ Z\chi_1^0\chi_1^0 $ result in SI and SD DM-nucleon scatterings in DM detection experiments, respectively. As shown in Fig. B1(a), B1(b), and B1(c), both the DM direct detection experiments for the SI and SD interactions set very stringent limits on the parameter space, and the two effects can be complementary in some parameter regions. We can observe that some parameter regions are still permitted by the direct detection with$ y_1\sim y_2 $ . In this case, the$ h\chi_1^0\chi_1^0 $ and$ Z\chi_1^0\chi_1^0 $ couplings are suppressed.The results of the DTFDM model shown in Fig. B2 are similar to those of the SDFDM model in Fig. B1. Since both the doublets and triplet participate in the weak interaction, the DM in the DTFDM model would always have a significant annihilation cross section. When DM is not very light, a small DM relic density can be easily achieved in the DTFDM model. If
$ M_S $ is replaced by$ M_T $ , the mass matrix$ M_N $ of the neutral NP particles in the DTFDM model is identical to that in the SDFDM Eq. (5). Thus, the couplings of$ h\chi_1^0\chi_1^0 $ and$ Z\chi_1^0\chi_1^0 $ in these two models are equal when$ M_S=M_T $ for the same$ y_1 $ ,$ y_2 $ , and$ M_D $ . Therefore, the excluded regions set by the direct detection are the same in Fig. B1(a) and Fig. B2(a).
Exploring fermionic multiplet dark matter through precision measurements at the CEPC
- Received Date: 2022-02-17
- Available Online: 2022-09-15
Abstract: New physics could be explored through loop effects using the precision measurements at the Circular Electron Positron Collider (CEPC) owing to its clean collision environment and high luminosity. In this paper, we focus on two dark matter models that involve additional electroweak fermionic multiplets. We calculate their one-loop corrections in five processes, i.e.,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: