-
Photonuclear reactions play an important role in basic and applied nuclear physics research [1–4]. The development of both nuclear physics research and applications based on photonuclear reactions is closely related to the development of attendant photon sources and measuring instruments. The mechanism behind photonuclear reactions changes according to the energy of the incident photons. However, to date, most photonuclear reactions have been studied in terms of bremsstrahlung photons in the energy range of 10–30 MeV [5–8] and have involved the use of medical electron linear accelerators (linacs). In this energy range, only simple reactions, such as (γ,n), (γ,2n), and (γ,p), can take place [5, 9–11], with the compound reaction mechanism playing a dominant role. At higher energies, the nuclear reaction processes become more complex [12–15]; this means that the measurement and analysis of experimental data related to, for example, reaction cross sections and/or reaction yields can help expand our understanding of specific aspects (for example, reaction mechanisms and reaction channel effects) and provide useful nuclear data for application purposes. Therefore, the study of multiparticle reactions occurring via bremsstrahlung radiation with end-point energies above the giant dipole resonance (GDR) region, that is, >30 MeV, is gaining an increasing amount of attention [16–19].
In this study, photonuclear reactions occurring on specific strontium (Sr) target nuclei were selected for examination. Natural strontium consists of four stable isotopes with the following mass numbers and isotopic abundances: 84Sr (0.56%), 86Sr (9.86%), 87Sr (7.00%), and 88Sr (82.58%). Although all of these isotopes can undergo photodisintegration via different reaction channels, only a small number have been studied thus far, namely, 86Sr(γ,n)85m,gSr [20–25], 86Sr(γ,pn)84m,gRb [25], and natSr(γ, xn)85m,gSr [26]. With the exception of our previous work [26], wherein multiparticle reactions on natural strontium were studied using end-point energies of 55, 60, and 65 MeV, all other previous research [20–25] investigated only single reactions on the 86Sr stable isotope using bremsstrahlung end-point energies of <30 MeV. Thus, to obtain more information regarding reactions with a higher degree of complexity, this study investigated multiple nucleon emission reactions on natural strontium target nuclei, expressed as natSr(γ, xnyp), using bremsstrahlung end-point energies of 55, 60, and 65 MeV, where x and y are the numbers of neutrons and protons emitted with a value ≥1.
This study aimed to identify the reaction products formed in natSr(γ, xnyp) reactions, determine their production yields, and clarify the relationship between the reaction yields and incident energies. The reaction yield was determined from the measured activity of the final reaction product using the activation method in combination with induced activity measurements from off-line γ-ray spectroscopy. This experimental method has several advantages, including a simple experimental setup and inexpensive instrumentation compared with certain online measurements, and it also allows for the unambiguous identification of individual reactions and radioisotopes formed in multiple nucleon emission reactions based on their half-lives and γ-ray energies.
In addition to the measurements, the production yields of residual nuclides formed in the natSr(γ, xnyp) reactions were calculated using the code TALYS-1.95 [27] in conjunction with various level-density models. The calculated results were compared with the experimental outcomes to determine which density model provided the best fitting. Under the aforementioned experimental conditions, the yields of the radionuclides 82Sr, 83(m+g)Sr, 85mSr, 85gSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83gRb, 84(m+g)Rb, and 86(m+g)Rb produced in the natSr(γ,xnyp) reactions were identified and determined. Studying the production yields of multiparticle reactions can help to better understand how the resulting reaction yields vary depending on the incident energy and the complexity of the nuclear reactions. In addition, specific reaction products are potential medical isotopes, namely, 87mSr [28], 85Sr [29, 30], 83Sr [31], 82Rb/82Rb generator [32, 33], and 81Rb [34]; this means that studying the reaction yields is useful for both research and application purposes.
The experiments were conducted using the 100-MeV electron linac at the Pohang Accelerator Laboratory (PAL), POSTECH, Korea, and the bremsstrahlung radiation was generated by bombarding 55-, 60-, and 65-MeV electrons onto a thin tungsten (W) target. The required radioactivity of the irradiated samples to determine the yield of the individual reaction was measured via off-line γ-ray spectrometry using a high-purity germanium (HPGe) detector [18, 35–36]. The measurement of the production yields for the radionuclides produced in the natSr(γ, xnyp) reactions is the first of its kind.
-
Three samples of extra-pure strontium nitrate (Sr[NO3]2) powder with masses between 1,100 and 1,200 mg were prepared for irradiation by packing them in a 1.2 × 1.2-cm box composed of high-purity aluminum foil. Irradiation was performed using the PAL test linac. Details of the electron linac and bremsstrahlung production are provided in [37] and [38]. The bremsstrahlung photons were produced by bombarding accelerated electron beams at the desired energy onto a W target with dimensions of 100 × 100 mm and a thickness of 0.1 mm. The W target was positioned 15 cm from the electron beam exit window. In the experiments, three separate irradiations were performed with bremsstrahlung photon end-point energies of 55, 60, and 65 MeV. The sample was placed 12 cm from the W target along the axis of the electron beam, and the electron linac was maintained at stable operation with an electron beam current of 25 mA, a beam pulse width of 1.2 μs, and a repetition rate of 30 Hz for all irradiations. The duration of each irradiation was 3 h.
-
The γ spectra of the irradiated Sr(NO3)2 samples were measured using a γ-ray spectrometer with a coaxial HPGe detector (model ORTEC, GEM-20180-p) connected to a PC-based 4K channel analyzer. The energy resolution of the detector was 1.8 keV at the 1,332.5 keV γ-peak of 60Co, and the detection efficiency was 20% at 1,332.5 keV compared with that of a 7.6 cm × 7.6 cm NaI(Tl) detector. The efficiency of the HPGe detector as a function of the γ-ray energies and distance between the sample and the detector were calibrated using the following set of standard γ sources: 241Am (59.541 keV), 137Cs (661.657 keV), 60Co (1,173.237 keV and 1,332.501 keV), 152Eu with γ-ray energies of 121.8–1,408 keV, and 133Ba with γ-ray energies of 53.16–388.85 keV. For the γ activity measurements, the activated sample was placed at least 10 cm from the detector surface to maintain the detector dead time at approximately 5% and to reduce counting losses due to the coincidence summing effect.
The half-lives of previously studied radionuclides vary from 67.6 m (85mSr) to 86.2 days (83gRb). Thus, a series of γ-ray spectra were measured at different waiting times, from tens of minutes to several days following irradiation, to determine the half-lives of specific radionuclides and select the appropriate spectra for the determination of the activity for each isotope. A typical γ-ray spectrum of the irradiated Sr(NO3)2 sample is shown in Fig. 1, with the γ-ray spectrum recorded 21 h after irradiation. The measured γ-spectra were analyzed using GammaVision software, version 5.10 (EG&G ORTEC). The radionuclides produced were identified based on their characteristic γ-ray energies and half-lives. The nuclear reaction channels that can lead to the studied radionuclides and their main γ-ray energies and intensities used to determine the yield of the reaction products are given in Table 1. The nuclear data given in columns 4–7 of Table 1 are taken from Ref. [39]. In Ref. [39], we can also find additional important nuclear data, including energy level diagrams for the decay scheme of many radionuclides.
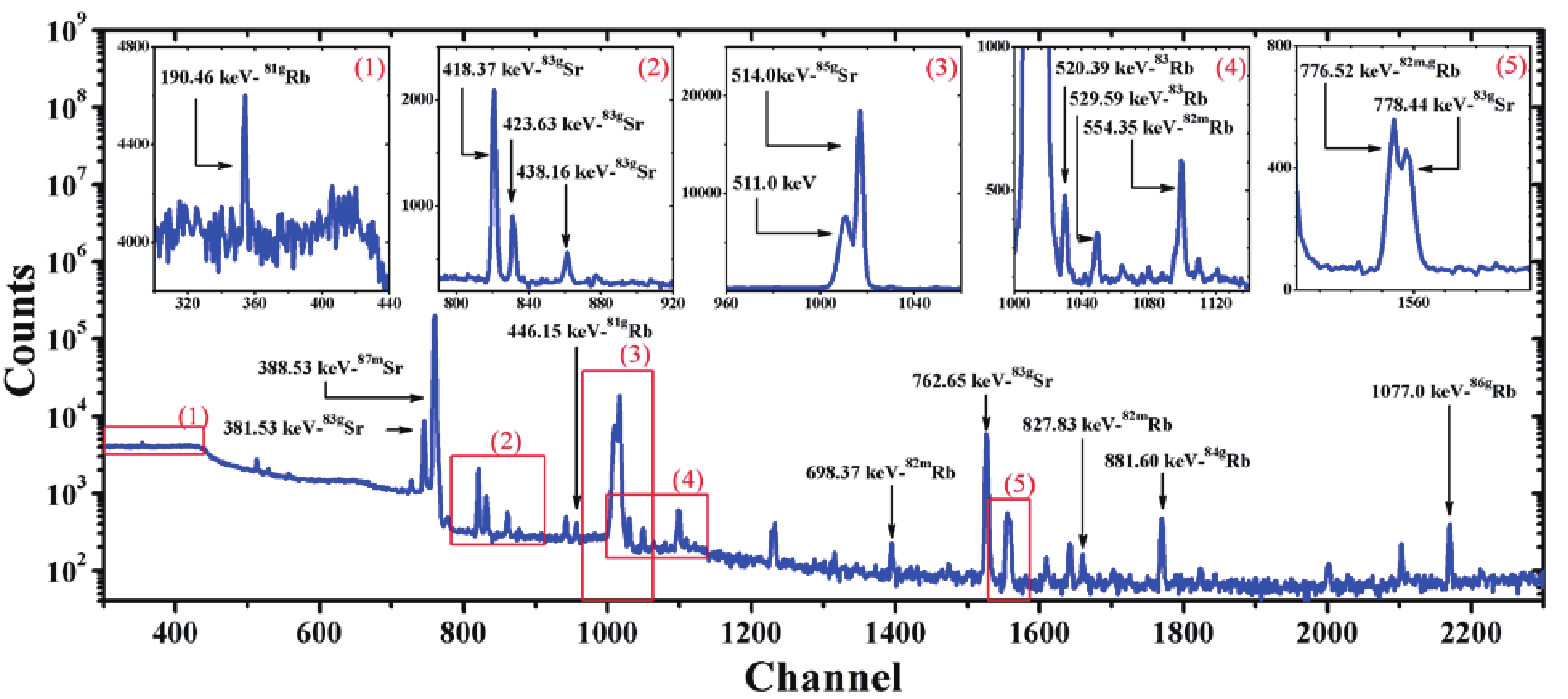
Figure 1. (color online) Gamma spectrum of the natSr(NO3)2 sample irradiated with 60 MeV bremsstrahlung end-point energy with an irradiation time of 3 h, a waiting time of 21 h, and a measurement time of 1.5 h.
Reaction product Contributing reaction Threshold energy,
Eth/MeVHalf-life,
T1/2Decay mode
(%)γ-ray energy,
Eγ/keVγ-ray intensity,
Iγ (%)87mSr 88Sr(γ,n) 11.11 2.815 h IT:99.70
ε: 0.30388.53 82.19 85mSr 88Sr(γ,3n)
87Sr(γ,2n)
86Sr(γ,n)31.04
19.92
11.4967.6 min IT:86.6
ε:13.4151.19
231.8612.8
83.985gSr 88Sr(γ,3n)
87Sr(γ,2n)
86Sr(γ,n)31.04
19.92
11.4964.84 d ε:100 514.0 96 83gSr 88Sr(γ,5n)
87Sr(γ,4n)
86Sr(γ,3n)
84Sr(γ,n)51.49
40.38
31.95
11.9232.41 h ε:100 381.53
418.37
423.63
438.16
762.65
778.4414.0
4.2
1.44
0.77
26.7
1.7682Sr 88Sr(γ,6n)
87Sr(γ,5n)
86Sr(γ,4n)
84Sr(γ,2n)60.34
49.23
40.80
20.7825.35 d ε:100 − − 86gRb 88Sr(γ,1p1n)
87Sr(γ,1p)20.54
9.4218.64 d β:~100 1077.0 8.64 84gRb 88Sr(γ,1p3n)
87Sr(γ,1p2n)
86Sr(γ,1p1n)39.67
28.56
20.1332.82 d ε: 96.1 511.0
881.6051.4
68.983gRb 88Sr(γ,1p4n)
87Sr(γ,1p3n)
86Sr(γ,1p2n)
84Sr(γ,1p)48.44
37.32
28.94
8.8786.2 d ε: 100 520.39
529.59
552.5545
29.3
16.082mRb 88Sr(γ,1p5n)
87Sr(γ,1p4n)
86Sr(γ,1p3n)
84Sr(γ,1p1n)59.40
48.28
39.85
19.826.472 h ε: 100 554.35
698.37
776.52
827.8362.4
26.3
84.39
21.081gRb 87Sr(γ,1p5n)
86Sr(γ,1p4n)
84Sr(γ,1p2n)57.09
48.66
28.634.572 h ε: 100 190.46
446.1564.9
23.5Table 1. Nuclear reactions studied and main decay data of the reaction products [39].
To determine the reaction yield, the activity of the residual nuclide must be ascertained via conversion from the net counts/area (Sγ) under the photopeak of the selected γ-ray, namely, A = Sγ/(Iγ . εγ), where A is the activity of the residual radionuclide, Iγ is the branching ratio/intensity of the γ-ray, and εγ is the energy-dependent detection efficiency of the detector. In general, the activity is measured using the most intense, well-separated, and interference-free/-correctable γ-ray. Details of the activity measurements for each radionuclide produced in the natSr(γ, xnyp) reactions are provided below.
The activity of 87mSr (T1/2 = 2.815 h) was measured using γ-rays of 388.53 keV (82.19%). However, there were three other γ-rays with energies close to 388.53 keV, namely, 389.37 keV (1.50%) from 83gSr (T1/2 = 32.41 h), 389.4 keV (0.08%) from 82mRb (T1/2 = 6.472 h), and 388.85 keV (0.46%) from 81Rb (T1/2 = 4.572 h). The investigation revealed that the contribution of 389.4 keV (0.08%) γ-rays from 82mRb and 388.85 keV (0.46%) γ-rays from 81Rb was negligible, meaning only the contribution of 389.37 keV (1.50%) γ-rays from 83gSr required correction. The count numbers under the photopeak area of the 389.37 keV (1.50%) γ-rays were derived from those of the 418.37 keV (4.2%) γ-rays emitted by the same 83gSr isotope based on the following relationship [40, 41]:
$ {{{S_{(389.37)}}} \mathord{\left/ {\vphantom {{{S_{(389.37)}}} {{S_{(418.37)}}}}} \right. } {{S_{(418.37)}}}} = ({{{I_{(389.37)}} \times {\varepsilon _{(389.37)}})} \mathord{\left/ {\vphantom {{{I_{(389.37)}} \times {\varepsilon _{(389.37)}})} {({I_{(418.37)}} \times {\varepsilon _{(418.37)}})}}} \right. } {({I_{(418.37)}} \times {\varepsilon _{(418.37)}})}} , $

(1) where S, I, and ε represent the net counts/photopeak area, branching ratio/intensity, and energy-dependent detection efficiency of the detector, respectively. The subscripts (389.37) and (418.37) denote the energies of the corresponding γ-rays.
After obtaining the photopeak area for the 389.37 keV γ-rays based on Eq. (1) and subtracting it from the common peak at 388.53–389.37 keV, the actual peak area for the γ-rays of 388.53 keV was obtained. From this, the activity of 87mSr could be inferred based on the known intensity and detection efficiency of the 388.53 keV γ-rays.
The activities of 85mSr and 85gSr were measured separately, with the activity of the former (T1/2 = 67.63 min) measured using γ-rays of 231.86 keV (83.9%) starting from 1–2 h after irradiation. The energy of the γ-ray used for activity measurement was relatively low; therefore, a correction for self-attenuation was performed. The self-attenuation factor, katt, was approximated using the following equation:
$ {k_{\rm att}} = {{(1 - {{\rm e}^{ - \mu d}})} \mathord{\left/ {\vphantom {{(1 - {{\rm e}^{ - \mu d}})} {\mu t}}} \right. } {\mu t}} $

(2) where μ is the linear attenuation coefficient of the γ-ray, and t is the thickness of the sample.
The activity of 85gSr (T1/2 = 64.849 d) was measured using γ-rays of 514 keV (96%). While this value was close to 511 keV, these two photopeaks could be separated via fitting. Because the half-life of 85gSr is comparatively long, the measurements of its activity were initiated a few days following irradiation to reduce spectral background below the photopeak of 514 keV. Furthermore, because the 85mSr isomeric state decays to the 85gSr ground state with an isomeric transition (IT) coefficient of 86.6%, the measured activity based on the 514 keV γ-rays is cumulative. Therefore, to obtain the independent activity of 85gSr, the contribution of 85mSr was subtracted based on the procedure described in our previous work [26].
The 83Sr radionuclide exists in both isomeric and unstable ground states. Because the half-life of the isomeric state of 83mSr (T1/2 = 4.95 s) is short, its activity could not be measured, whereas the activity of the unstable ground state of 83gSr (T1/2 = 32.41 h) could be measured using the interference-free γ-rays of 762.65 keV (26.7%). Given that 83mSr decays to 83gSr with an IT coefficient of 100%, the activity measured from the γ-rays of 762.65 keV was accumulated and used to determine the yield of 83(m+g)Sr.
The activity of 82Sr (T1/2 = 25.34 d) cannot be measured directly because it does not emit γ-rays. However, 82Sr decays to 82gRb (T1/2 = 1.2575 min) with a β decay factor of 100%, and 82gRb emits γ-rays of 776.52 keV (15.08%), which could be used to measure its activity. The half-life of 82gRb is short compared with that of 82Sr; therefore, these two radionuclides are considered to be in equilibrium, which means that the activity of 82Sr could be measured indirectly via the 776.52 keV γ-rays from 82gRb. While the 776.52 keV γ-ray is close to 775.77 keV (0.056%) and the 778.44 keV (1.76%) γ-rays of 83gSr (T1/2 = 32.41 h), separation could be performed via fitting. Finally, the contribution of 82mRb to the common peak of 776.52 keV could be estimated from other γ-rays (for example, 698.37 keV [26.3%] or 827.83 keV [21.0%]) emitted by the same isotope (82mRb) [40, 41] using Eq. (1) and subsequent subtractions.
The 86Rb radionuclide exists in both isomeric and unstable ground states; the half-life of the 86mRb (T1/2 = 1.017 min) isomeric state is short, meaning its activity cannot be measured, whereas the activity of the ground state 86gRb (T1/2 = 18.64 d) can be measured using 1,077.0 keV (8.64%) γ-rays. Here, given that the 86mRb isomeric state decays to the 86gRb ground state with an IT coefficient of 100%, the activity measured using the 1,077.0 keV γ-rays represents the cumulative activity of 86(m+g)Rb.
The 84Rb radionuclide also exists in both isomeric and unstable ground states, and because the half-life of the isomeric state 84mRb (T1/2 = 20.26 min) is relatively short, it is not suitable for current measurements requiring a long waiting time to reduce γ-spectral background. However, for the ground state 84gRb (T1/2 = 32.82 d), the interference-free γ-ray of 881.60 keV (68.9%) was suitable for the activity measurement. Here, given that 84mRb decays to 84gRb with an IT coefficient of 100%, the measurement using an 881.60 keV γ-ray represents the cumulative activity for 84(m+g)Rb.
The 83gRb (T1/2 = 86.2 d) radionuclide emits three γ-rays of suitable energy and intensity for corresponding activity measurements (see Table 1); however, there was an interference problem with two of these, with the photopeak of 520.39 keV γ-rays significantly affected by the tail of the 511–514 keV photopeak, while the photopeak at 552.55 keV was disturbed by that of 554.35 keV (62.4%) from 82mRb. Therefore, to avoid complicated corrections, the γ-ray of 529.5945 keV (29.3%) was selected to measure the activity for 83gRb. Knowing that the 83gSr (T1/2 = 32.41 h) radionuclide decays to 83gRb with a decay factor of 100%, the contribution from 83gSr was corrected.
The 82Rb radionuclide exists both in an isomeric state 82mRb (T1/2 = 6.742 h) and unstable ground state 82gRb (T1/2 = 1.2575 min), and because the half-life of 82gRb is relatively short, it rapidly entirely decays into the stable isotope 82Kr following irradiation. Therefore, its activity could not be measured. The 82mRb radionuclide emits a number of γ-rays (see Table 1), some of which are interference free. In this study, the activity of 82mRb was measured using γ-rays of 698.37 keV (26.3%) and 827.83 keV (21.0%).
The 81Rb radionuclide also exists both in an isomeric state 81mRb (T1/2 = 30.5 m) and unstable ground state 81gRb (T1/2 = 4.572 h), and because 81mRb has a relatively short half-life and low γ-ray energy and intensity, it is impossible to measure its activity with sufficient accuracy. Therefore, in this study, only the activity of 81gRb was measured, with the measurement performed using the most intense γ-ray of 190.46 keV (64.9%), which was not disturbed by the other γ-rays. Because the 81mRb radionuclide decays to 81gRb with an IT coefficient of 97.60%, the activity measured using a γ-ray of 190.46 keV is cumulative, and the yield derived from the current measured activity represents the radionuclide 81(g+0.976m)Rb.
-
In general, the yield of a specific reaction product is defined as the number of residual nuclei produced per second (1/s), as described in [5].
$ {Y_k} = {N_a}\int_{{E_{\rm th}}}^{{E_{\gamma \max }}} {{\sigma _k}\left( E \right)\phi \left( E \right){\rm d}E}, $

(3) where Na is the number of target atoms in the sample, Eth is the reaction threshold energy, and Eγmax is the maximum bremsstrahlung energy. The terms σ(E) and ϕ(E) represent the energy-dependent reaction cross section and bremsstrahlung flux at the sample position, respectively.
In terms of experimentation, the reaction yield can be derived from the measured activity of the reaction product; however, in terms of practical application, the production yield is generally expressed in units of
$\rm kBq \cdot \mu {A^{ - 1}} \cdot {h^{ - 1}} \cdot m{g^{ - 1}}$ . To achieve this, the yield is determined based on the following expression:$ {Y_{\exp }} = \frac{{{S_\gamma }\lambda }}{{{I_\gamma }{\varepsilon _\gamma }Fk}}\frac{1}{{{m_{\rm Sr}}{I_e}{t_i}}} ,$

(4) where Sγ is the number of counts under the photopeak of the selected γ-ray accumulated during the measurement period, λ is the decay constant of the produced isotope, Iγ and εγ are the intensity and energy-dependent detection efficiency of the γ-ray, respectively, k is the correction factor for counting losses, mSr is the mass of the strontium element in the compound sample Sr(NO3)2, Ie is the electron beam current from the exit window of the accelerator, and ti is the irradiation time. The factor F is given by Eq. (5).
$ F = (1 - {{\rm e}^{ - \lambda \tau }}){{\rm e}^{ - \lambda (T - \tau )}}(1 - {{\rm e}^{ - \lambda {t_i}}}){{\rm e}^{ - \lambda {t_w}}}(1 - {{\rm e}^{ - \lambda {t_m}}})/{{\rm e}^{ - \lambda T}}, $

(5) where τ is the pulse width of the electron beam, T is the cycle period, and ti, tw, and tc are the irradiation, waiting, and measuring times, respectively.
-
To predict the yield of the reaction product induced by bremsstrahlung photons, it is necessary to calculate the reaction cross section and simulate the bremsstrahlung spectrum flux. In this study, the energy-dependent cross section of the investigated reaction was calculated based on the TALYS-1.95 code [27], whereas the bremsstrahlung spectrum was simulated using the Monte Carlo N–Particle Transport Code System software [42]. The simulation of the bremsstrahlung spectrum was performed using the experimental geometry described in section II.B. Three bremsstrahlung spectra were produced by the impingement of electron beams of 50, 60, and 65 MeV on a thin W target and the cross section as a function of the energy of the possible reactions occurring on natural strontium leading to the formation of the following reaction products: 82Sr, 83(m+g)Sr, 85m,gSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83Rb, 84(m+g)Rb, and 86(m+g)Rb, as shown in Fig. 2.
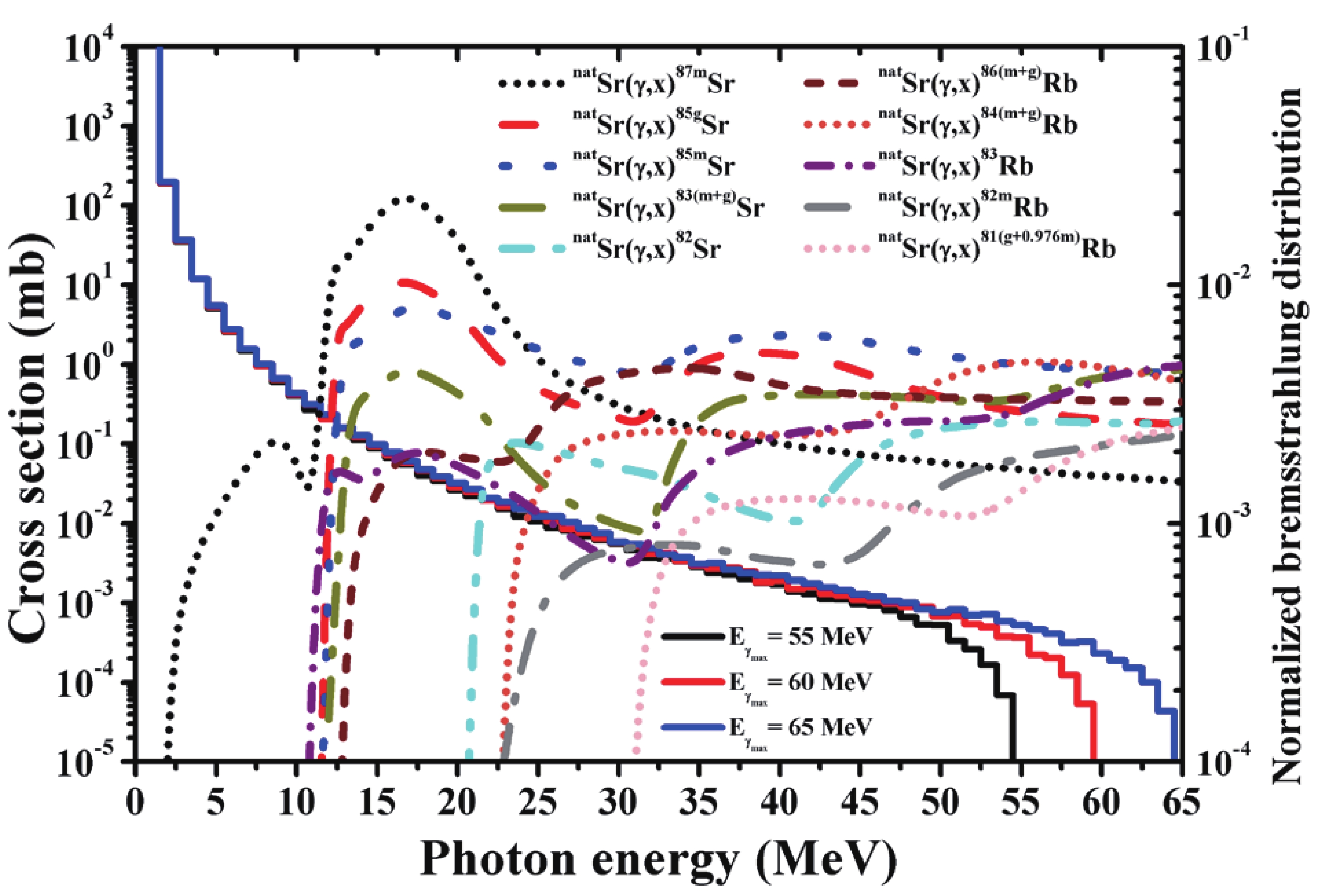
Figure 2. (color online) Simulated bremsstrahlung spectra emitted by the impingement of 55-, 60-, and 65-MeV electron beams on a thin W target (100 × 100 mm, thickness = 0.1 mm), and the excitation function for the production of 82Sr, 83(m+g)Sr, 85mSr, 85gSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83Rb, 84(m+g)Rb, and 86(m+g)Rb radionuclides via the natSr(γ,xnyp) reactions calculated using the TALYS-1.95 code.
As noted, natural strontium consists of four stable isotopes, which can participate in nuclear reactions to form the same radionuclide via different reaction channels (see Table 1). Therefore, when calculating the production yield for each reaction product, all possible reaction channels were considered. The total cross-section value was obtained by summing the individual cross sections of all the reaction channels leading to the same reaction product. Fig. 3 presents an example of the total cross sections and all the individual cross sections of the possible reaction channels that can be formed on the stable isotopes 86Sr, 87Sr, and 88Sr and lead to the formation of 84mRb, 84gRb, and 84(m+g)Rb.
According to the experimental conditions under which the accelerator was operated in pulsed mode, the studied strontium element consisted of four stable isotopes and was present in the Sr(NO3)2 sample. The theoretical yield of the corresponding photonuclear reaction was calculated as follows:
$ {Y_{\rm cal}} = \sum\nolimits_i {{\zeta _i}\frac{1}{{{m_{\rm Sr}}{I_e}T}}{N_{\rm Sr}}} \delta \int_{{E_{\rm th}}}^{{E_{\gamma \max }}} {{\sigma _i}(E)\phi (E) {\rm d}E}, $

(6) where i (= 1–4) represents the number of stable Sr isotopes that participated in the reaction, mSr is the mass, NSr is the number of Sr nuclei in the Sr(NO3)2 sample, ζi is the isotopic abundance of the stable Sr isotopes, Ie is the electron beam current from the exit window of the electron linac, T is the cycle period of the accelerated electron beam, Eth and Eγmax are the reaction threshold and end-point energy of the bremsstrahlung spectrum, respectively, σi(E) is the energy-dependent cross section of the individual reaction, and φ(E) is the bremsstrahlung spectral flux passing through the sample with an area of 1.44 cm2. The factor δ represents the fraction that a bremsstrahlung photon will interact with a strontium atom in Sr(NO3)2, knowing that a molecule of Sr(NO3)2 consists of nine atoms (one strontium atom, two nitrogen atoms, and six oxygen atoms) and assuming that the probability of these atoms interacting with a photon is the same.
It should be noted that one of the most important parameters used in the calculation based on the TALYS-1.95 code [27] is the nuclear level-density model. To investigate the influence of level-density models on the cross section and yield calculation results and identify the most consistent level-density model via comparisons with the experimental data, the calculations were performed using both phenomenological and microscopic level density models, namely, the constant temperature Fermi gas model (CTFGM), backshifted Fermi gas model (BSFGM), generalized superfluid model (GSFM), microscopic nuclear level-density model (Skyrme force) from Goriely's table (SFGM), microscopic nuclear level-density model Skyrme force from Hilaire’s combinatorial tables (SFHM), and microscopic nuclear level-density model (temperature dependent HFB, Gogny force) from Hilaire’s combinatorial tables (GFHM). The γ-ray strength function (
γSF), a nuclear statistical quantity used for a γ-emission channel in nuclear reactions (especially compound nuclear reactions), was a further consideration. In the TALYS program, the γSF model is applied based on the Hauser–Feshbach model to calculate the competition between photons and other particles with a standard Lorentzian form of the GDR (Brink-Axel option) [27]. The cross sections obtained based on a combination of the γSF model and CTFGM are shown in Figs. 2 and 3. The results obtained using the different level-density models were compared with the experimental data and are discussed in the following section. 
Figure 3. (color online) Cross sections of possible reaction channels on natural strontium: the cross section of the reactions of (a) 88Sr(γ,x)84m,gRb, 87Sr(γ,x)84m,gRb, 86Sr(γ,x)84m,gRb, and natSr(γ,x)84(m+g)Rb; (b) 88Sr(γ,x)84m,gRb, 88Sr(γ,p3n)84m,gRb, 88Sr(γ,d2n)84m,gRb, and 88Sr(γ,tn)84m,gRb; (c) 87Sr(γ,x)84m,gRb, 87Sr(γ,p2n)84m,gRb, 88Sr(γ,dn)84m,gRb, and 88Sr(γ,t)84m,gRb; and (d) 86Sr(γ,x)84m,gRb, 86Sr(γ,pn)84m,gRb, and 86Sr(γ,d)84m,gRb.
-
The experimental yields of the 82Sr, 83(m+g)Sr, 85mSr, 85gSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83gRb, 84(m+g)Rb, and 86(m+g)Rb radionuclides produced in the natSr(γ, xnyp) reactions with bremsstrahlung end-point energies of 55, 60, and 65 MeV are presented in columns 2–4 of Table 2. Here, the majority of the results involved errors in the range of 9%–15%, with the main sources of uncertainty being the statistical error (3%–6%), the determination of the γ-peak area (4%–7%), the nuclear data used in the calculations (4%–7%), the efficiency of the detector (3%–4%), the variation of the electron beam (5%–8%), and another source of error that could not be accurately determined (4%–6%). Radioactive Sr isotopes were clearly formed in the natSr(γ,xn) photoneutron reactions, with 1–6 neutrons emitted from the target nucleus. Various Rb isotopes were formed in the multiparticle natSr(γ,xnyp) reaction, wherein one proton (y = 1) was emitted along with 1–5 neutrons. For comparison, the theoretical yield values of the natSr(γ,xnyp) reactions calculated using the TALYS-1.95 code in conjunction with the six level-density models are presented in Fig. 4 and Fig. 5 along with the experimental results. The yield values calculated using the CTFGM are reported in Table 2.
Reaction product Yield ( $\rm kBq\cdot\mu {A^{ - 1} }\cdot{h^{ - 1} }\cdot m{g^{ - 1} }$ )

Experimental Calculation (CTFGM) 55 MeV 60 MeV 65 MeV 55 MeV 60 MeV 65 MeV 87mSr 16.09 ± 1.93 16.39 ± 1.97 17.03 ± 2.04 16.84 17.42 17.56 85mSr 1.92 ± 0.25 2.04 ± 0.27 2.05 ± 0.27 1.97 2.05 2.07 85gSr 1.29 ± 0.19 1.44 ± 0.22 1.49 ± 0.22 1.35 1.41 1.47 83(m+g)Sr 0.18 ± 0.02 0.202 ± 0.022 0.22 ± 0.02 0.19 0.202 0.22 82Sr 0.023 ± 0.004 0.027 ± 0.005 0.029 ± 0.005 0.02 0.027 0.032 86(m+g)Rb 0.17 ± 0.03 0.21 ± 0.03 0.23 ± 0.04 0.17 0.18 0.19 84(m+g)Rb 0.048 ± 0.007 0.082 ± 0.012 0.102 ± 0.018 0.048 0.080 0.10 83gRb 0.040 ± 0.005 0.052 ± 0.006 0.071 ± 0.008 0.040 0.048 0.066 82mRb 0.00243 ± 0.00035 0.0044 ± 0.0006 0.0068 ± 0.0009 0.0024 0.0040 0.0066 81(g+0.976m)Rb 0.00241 ± 0.00035 0.0038 ± 0.0006 0.0059 ± 0.0009 0.0024 0.0038 0.0065 Table 2. Experimental and calculated yields of natSr(γ,x) reaction products produced using bremsstrahlung end-point energies of 55, 60, and 65 MeV. The calculations were performed using the TALYS-1.95 code in conjunction with the constant-temperature Fermi gas model (CTFGM) level-density model.
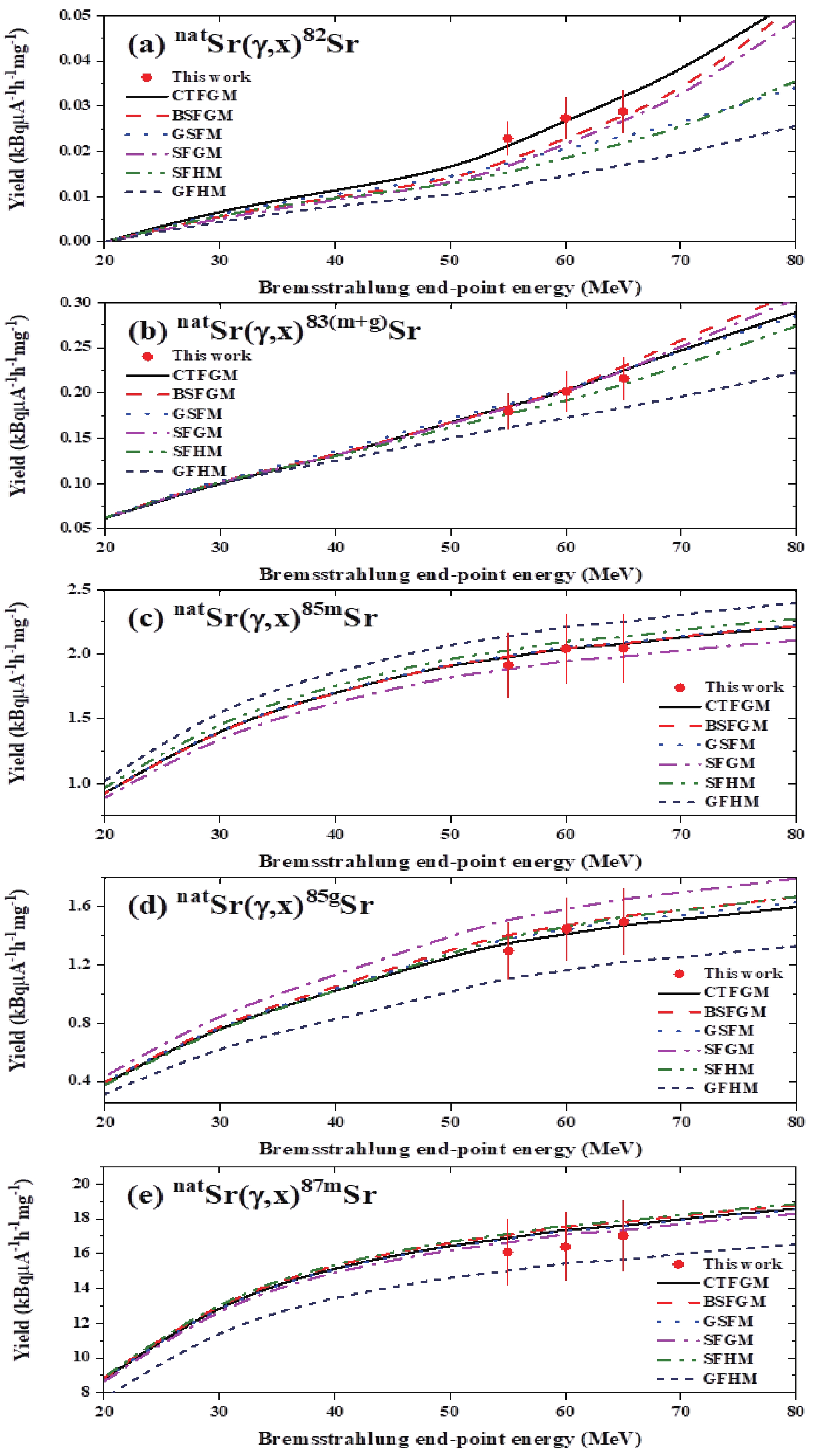
Figure 4. (color online) Measured and theoretically calculated yield values for the (a) natSr(γ,xn)82Sr, (b) natSr(γ,xn)83(m+g)Sr, (c) natSr(γ,xn)85mSr, (d) natSr(γ,xn)85gSr, and (e) natSr(γ,xn)87mSr reactions. The calculations were performed using the TALYS-1.95 code in conjunction with six different level-density models.
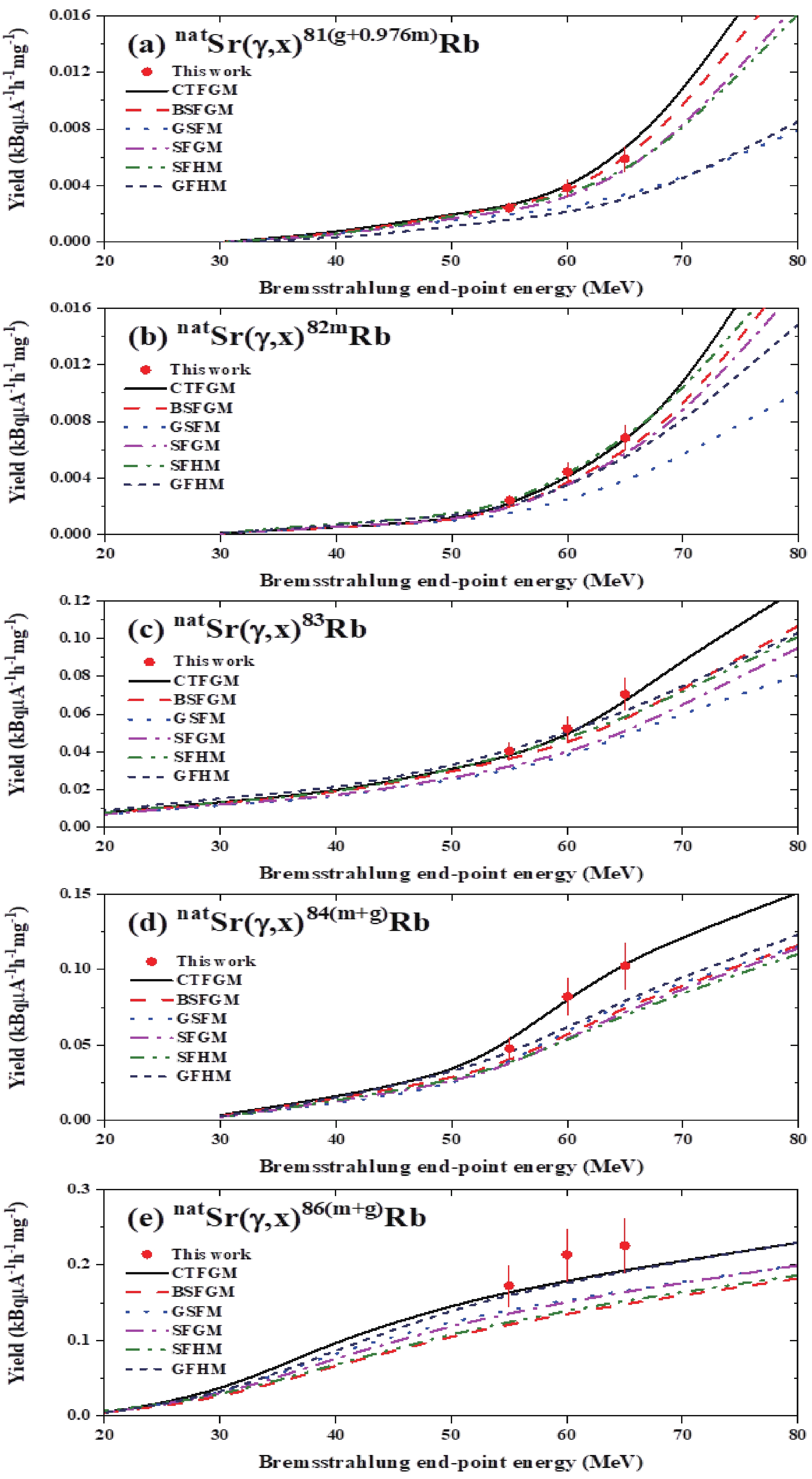
Figure 5. (color online) Measured and theoretically calculated yield values for the (a) natSr(γ,xnyp)81(g+0.976m)Rb, (b) natSr(γ,xnyp)82mRb, (c) natSr(γ,xnyp)83Rb, (d) natSr(γ,xnyp)84(m+g)Rb, and (e) natSr(γ,xnyp)86(m+g)Rb reactions. The calculations were performed using the TALYS-1.95 code in conjunction with six different level-density models.
As shown in Fig. 4 and Fig. 5, the yields calculated using the six models presented a similar shape to the experimental results. In addition, there was some agreement among the calculated results obtained using the different models. However, a detailed comparison indicated that the yields of the 82Sr, 83(m+g)Sr, 85m,gSr, 87mSr, 81(g+0.976m)Rb, and 82mRb radionuclides produced via natSr(γ,xnyp) reactions calculated using the GFHM differed significantly from the experimental results, whereas the yield values calculated using the TALYS-1.95 code in conjunction with the CTFGM were in good agreement with most of the experimental results, as shown in Fig. 6.
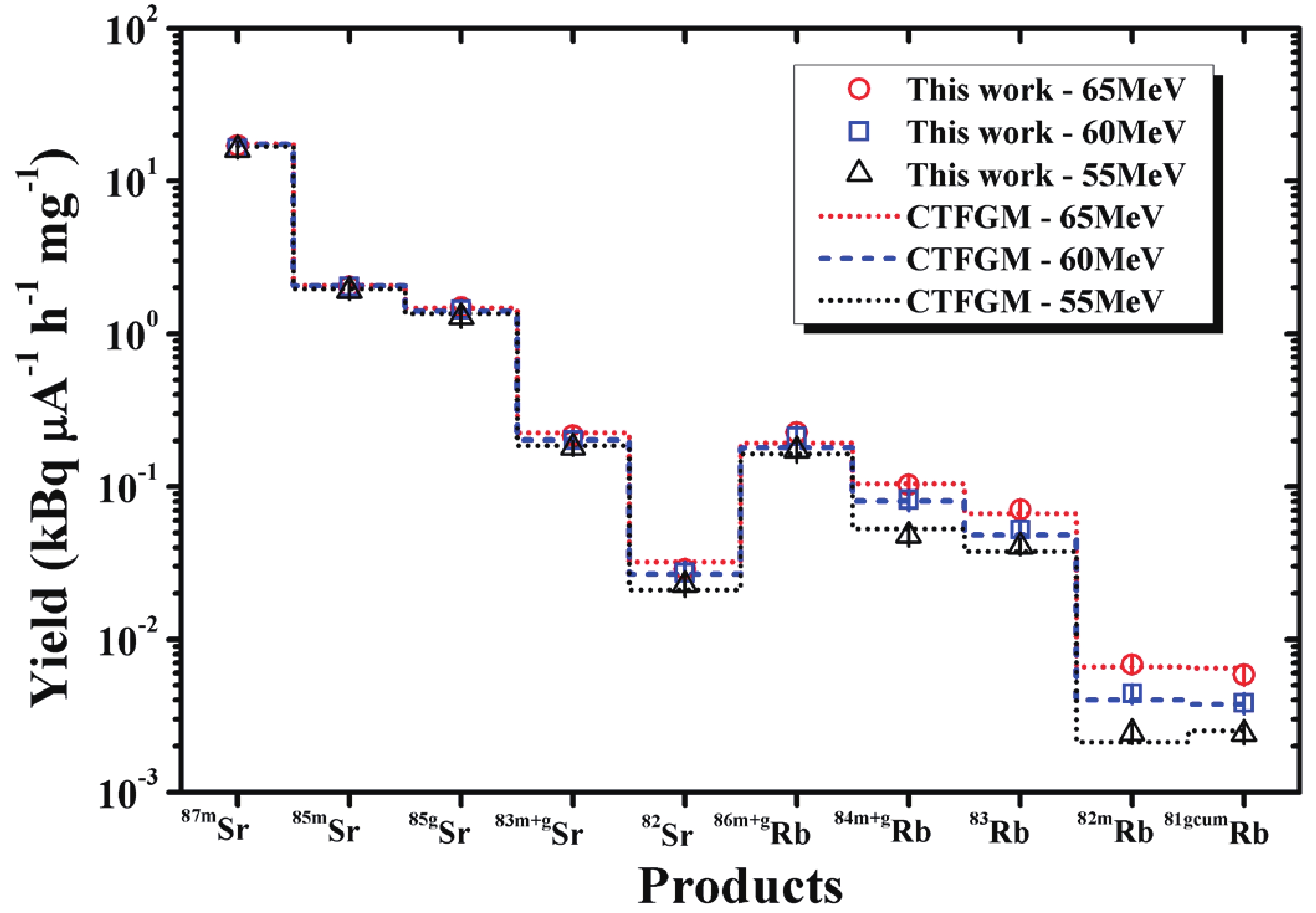
Figure 6. (color online) Experimental and calculated yields of natSr(γ,xnyp) reaction products with bremsstrahlung end-point energies of 55, 60, and 65 MeV. The calculation of the yield values was performed using the TALYS-1.95 code in conjunction with the constant-temperature Fermi gas model (CTFGM) level-density model.
In the studied energy range (55–65 MeV), the measured and calculated yields of radionuclides increased with an increase in excitation energy. However, at the same incident energy, a trend of lower yields emerged for reactions emitting more nucleons. In addition, by comparing the recognizable nuclear isobars of Sr and Rb produced in the natSr(γ,xnyp) reactions, it was clear that the yield of the Rb isobar produced by the natSr(γ,xnyp) reaction (in which one proton is emitted along with a number of neutrons) was approximately one order of magnitude lower than the yield of the Sr isobar formed by the natSr(γ,xn) photoneutron reaction. This could have been because proton emission processes are partially hindered by the Coulomb barrier.
-
This study conducted the first-ever measurement of the yields of the radionuclides 82Sr, 83(m+g)Sr, 85gSr, 85mSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83gRb, 84(m+g)Rb, and 86(m+g)Rb produced in the multiparticle reaction natSr(γ,xnyp) with bremsstrahlung end-point energies of 55, 60, and 65 MeV. The agreement between the experimental and calculated yields for all the radioisotopes was acceptable, except for the results calculated using the TALYS-1.95 code in conjunction with the GFHM level-density model. Specifically, the results calculated via the CTFGM level-density model were in good agreement with most of the experimental outcomes. In the studied energy range (55–65 MeV), both the measured and theoretically calculated results exhibited an increase in yield with an increase in bremsstrahlung end-point energy, which may have been due to the opening of new reaction channels with increasing reaction threshold energy. The yield of the multiparticle reactions decreased as the number of nucleons released from the target nucleus increased, that is, with increasing complexity of the reaction processes. In addition, it was also found that specific radioisotopes produced in natSr(γ,xnyp) reactions, including 87mSr, 85mSr, 83Sr, 82Sr/82Rb, and 81Rb, are promising medical isotopes. However, their production via photonuclear reactions on natural strontium has not yet been studied, with the exception of 85Sr generated via natSr(γ,xn)85Sr reactions. Therefore, in addition to providing new data on the nuclear yield of photonuclear reactions on natural strontium, the present study also provides an additional method for the production of useful medical isotopes.
-
The authors express their sincere gratitude to the Pohang Accelerator Laboratory for valuable support in conducting the experiments and its staff for excellent operation of the accelerator during experiments.
Multiparticle natSr(γ, ${\boldsymbol{xnyp}}$ ) reactions induced with bremsstrahlung end-point energies of 55, 60, and 65 MeV
- Received Date: 2022-04-06
- Available Online: 2022-09-15
Abstract: This study measured the yields of the radionuclides 82Sr, 83(m+g)Sr, 85mSr, 85gSr, 87mSr, 81(g+0.976m)Rb, 82mRb, 83gRb, 84(m+g)Rb, and 86(m+g)Rb produced in natSr(γ, xnyp) multiparticle reactions with bremsstrahlung end-point energies of 55, 60, and 65 MeV. The bremsstrahlung radiation was generated using the 100-MeV electron linear accelerator at the Pohang Accelerator Laboratory, Korea, and the reaction yields were derived from the induced activitiesmeasured using off-line γ-ray spectrometry. To obtain accurate experimental results, we performed the necessary γ-rayinterference corrections. The experimental results were compared with the theoretical predictions obtained usingthe TALYS-1.95 statistical nuclear model code. The calculations were performed using six different level-density models to ascertain which model best fitted the experimental results. The dependence of the reaction yield on the incident bremsstrahlung energy and on the number of nucleons emitted by the photonuclear reactions was also investigated.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: