-
The isospin quantum number, T, was introduced to characterize the nearly identical property of neutron and proton. Within the isospin formalism, neutron and proton are regarded as the same type of baryon with isospin
$ T = 1/2 $ , but with different projections,$ T_z(n) = 1/2 $ and$ T_z(p) = -1/2 $ , on the z axis in the isospin space. For a given nucleus with Z protons and N neutrons, its isospin projection is fixed and defined as$ T_z = (N - Z)/2 $ , while a number of states with$ T\geqslant |T_z| $ exists. In the nuclei with fixed mass number A, there exist isobaric analogue states (IASs) that exhibit the same intrinsic structure and total isospin T, but different isospin projection. These states form an isospin multiplet and provide a unique database to study the isospin symmetry.About half a century ago, it was noted that masses of an isospin multiplet can be described by a quadratic form of the well-known isospin multiplet mass equation (IMME) [1, 2]:
$ {\rm ME}(\alpha,T,T_{z}) = a(\alpha,T)+b(\alpha,T)T_{z}+c(\alpha,T)T_{z}^2, $

(1) where
${\rm ME} = (m - A{u})c^2$ is a mass excess of IAS of the multiplet with fixed A and T. Although the a, b, and c coefficients depend on A, T, and the other quantum numbers α such as the spin-and-parity$ J^{\pi} $ , respectively, they are independent of$ T_z $ . These coefficients reveal the strengths of the isoscalar, isovector, and isotensor components of the isospin-symmetry breaking interactions [3], and can be extracted from the masses of IASs. The global trends of a, b, and c as a function of A have been established in Refs. [4–6]. Any deviation from the regular systematics could be due to incorrect experimental masses of IASs [7] or new effects of isospin non-conserving forces [8].The validity of the quadratic form of IMME has been tested by using precise mass values of IASs [4–6]. This can be done by adding high-order terms, such as
$ d{T_z}^3 $ and/or$ e{T_z}^4 $ , to Eq. (1). The breakdown of the quadratic form of IMME is commonly attributed to the high-order perturbations, three-body interactions, and/or isospin mixing, etc. Although significant breakdowns have been found in several multiplets such as the$ A = 35 $ isospin quartet [9] and$ A=32 $ isospin quintet [10–12], the coefficients of the extra terms, d or e, are usually very small within a magnitude of keV, and the addition of the extra terms should not lead to a significant change in a, b, and c coefficients [13–16].Theoretical works have verified that the Coulomb interaction is the predominant contributor to the charge-dependent interactions, and consequently determines the values of the a, b, and c coefficients primarily. This simple and elegant mass equation is widely used as a powerful mass model to predict unknown masses where at least three masses of an isospin multiplet are known. The IMME predictions are particularly important for extremely neutron-deficient nuclei that are relevant in understanding the rapid proton capture process [17] and nuclear structure [18].
Although numerous studies have been conducted on the IMME, most of these studies concentrated on the isospin multiplet with
$ T \leqslant 2 $ . The investigation for more exotic isospin multiplets is insufficient owing to the lack of experimental information. In this study, the$ T=3, A=54 $ isospin septet is addressed, which consists of the lowest$ T = 3 $ states in 54Zn, 54Cu, 54Ni, 54Co, 54Fe, 54Mn, and 54Cr. In the recent evaluation of NUBASE2020 [19], the masses of$ T=3 $ IASs in 54Fe, 54Mn, and 54Cr are recommended based on experimental measurements. All information are summarized in Table 1. The a, b, and c coefficients of the$ A = 54 $ multiplet are calculated using the three known masses according to Eq. (1) and presented in Table 2. Using these parameters, the mass values of other four members of the$ A = 54 $ multiplet can be predicted in principle.Isotope Tz ME (g.s.)/keV Ex/keV ME(IAS)/keV 54Cr +3 −56935.38(13) 0 −56935.38(13) 54Mn +2 −55558.2(10) 6146.4(30) −49411.9(28) 54Fe +1 −56254.6(3) 14868(20) −41387(20) 54Zn* −3 −6504 (85) 0 −6504 (85) * Deduced from ground-state mass of 52Ni and the $Q_{2p}$ of 54Zn.

Table 1. Compilation of ME values for ground states (g.s.), IASs, and the corresponding excitation energy (
$E_x$ ) of the A = 54 isospin septet. All data are taken from NUBASE2020 [19] except for 54Zn.coefficient quadratic1 quadratic2 cubic2 a −32860.7(606) −33267.5(169) −32972.2(455) b −8777.0(512) −8431.9(137) −8572.6(243) c 250.7(104) 180.9(28) 139.2(66) d 18.6(27) $\chi^2/\nu$ 

49 1 Quadratic fit using 3 IASs, 54Fe, 54Mn and 54Cr.
2 Quadratic and cubic fits using 4 IASs, 54Fe, 54Mn 54Cr and 54Zn.Table 2. Fitted coefficients of the quadratic and cubic form of the IMME for the lowest A = 54, T = 3 isospin septet using ME values from Table 1. All coefficient values are in units of keV. In addition, the
$\chi^2/\nu$ value of the quadratic fit is also presented.The
$ T_z = -3 $ member of the$ A = 54 $ multiplet, 54Zn, is at the edge of the proton drip-line of zinc isotopes. This nuclide is of particular interest owing to its two-proton (2p) radioactivity, a rare decay mode that only emerges in nucleus with negative two-proton separation energy ($ S_{2p} $ ), but positive one-proton separation energy ($ S_p $ ).$ S_{2p} $ can be derived from the mass difference of the parent and daughter nuclei according to$ \begin{equation} S_{2p}(Z,A)={\rm ME}(Z-2,A-2)+2{\rm ME}(^1{\rm H})-{\rm ME}(Z,A), \end{equation} $

(2) with ME representing the mass excess of the nucleus.
The
$ 2p $ radioactivity of 54Zn was studied in two experiments. The$ 2p $ decay energy,$ Q_{2p} = - S_{2p} $ , was measured to be 1480(20) keV using silicon detectors in Ref. [20] and 1280(210) keV using gas electron multipliers in Ref. [21]. The results of these two experiments agree well with each other. Therefore, a weighted average value of 1478(20) keV was obtained for$ Q_{2p} $ of 54Zn. Recently, the ME value of 52Ni, the$ 2p $ decay daughter of 54Zn, was accurately measured to be –22560(83) keV, using the isochronous mass spectrometry at the HIRFL-CSR facility in Lanzhou [22]. Given the fact that the mass of proton is well known, the mass excess of 54Zn is deduced to be –6504(85) keV using the mass of 52Ni and the$ 2p $ decay energy of$ Q_{2p}=1478(20) $ keV. The deduced value of ME$ (^{54}{\rm{Zn}})=-6504(85) $ keV is presented in Table 1, and compared with the IMME prediction in Fig. 1. A significant difference as large as about 2 MeV is observed.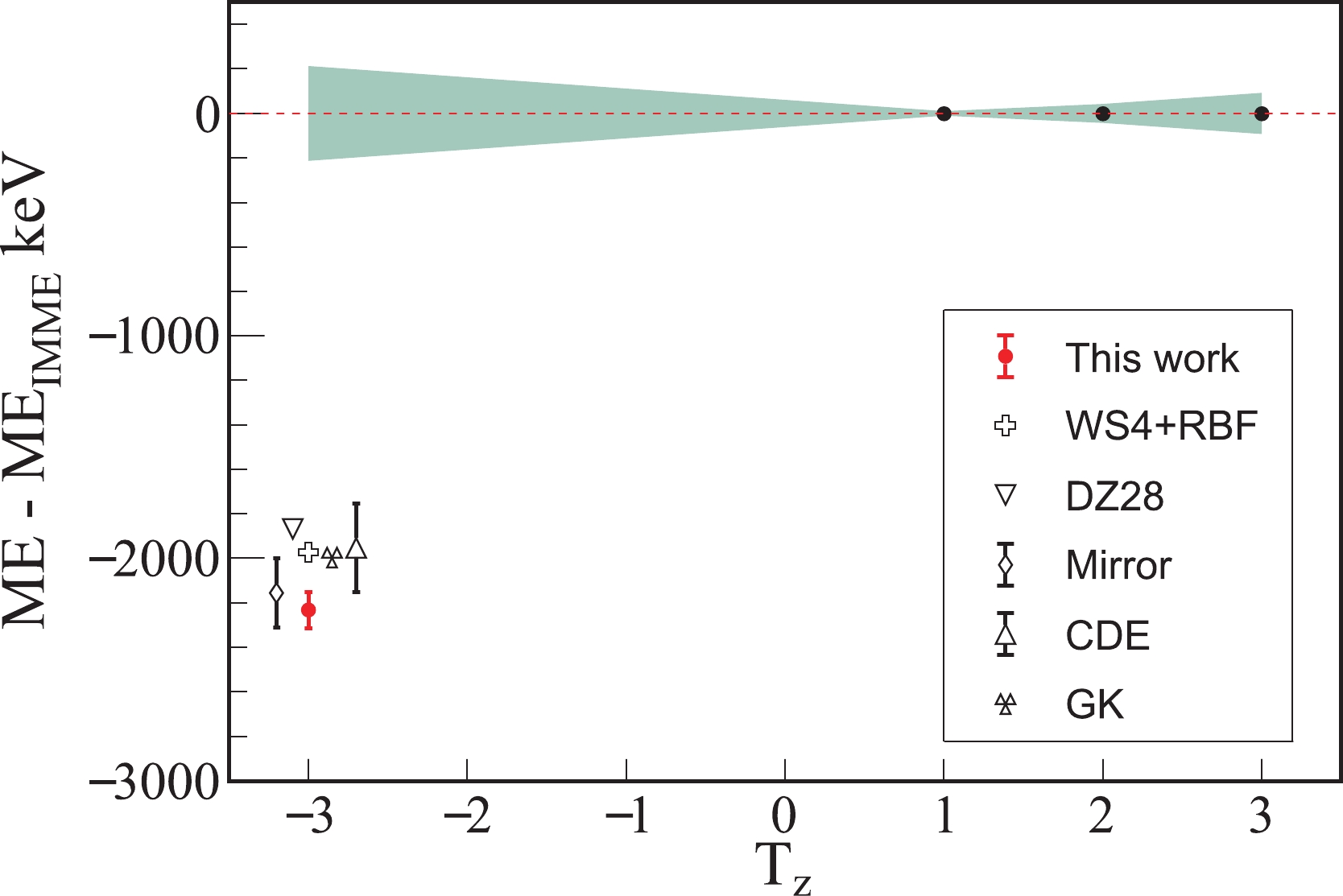
Figure 1. (color online) Mass difference between experimental values and predictions for 54Zn. The shading area represents the uncertainty from the IMME prediction.
Considering the reliable predictive power of IMME, this discrepancy is surprising. Fig. 1 also presents the predicted mass values of 54Zn from various mass models. Only the predicted masses from the latest version of WS4+RBF [23] and the Duflo and Zuker mass model (DZ28) [24] are adopted for comparisons in Fig. 1. The reason is that the two global mass models provide mass predictions with the smallest root mean square values of 200–600 keV in the
$ 28\leqslant Z \leqslant 50 $ mass region [25]. In addition, the predictions from several local mass models [26–28] are also compared in Fig. 1. The masses of neighboring or mirror nuclei are adopted in such local mass models, and the mass predictions are considered to have high accuracies [26–28]. For example, the mass predictions based on isospin symmetry have a root mean square value as small as approximately 100 keV [26] for the proton-rich nuclei.From Fig. 1, it can be observed that the predictions from the global and local mass models agree well with the presently deduced mass value of 54Zn within an uncertainty of 300 keV. However, the IMME prediction, which is commonly believed to be accurate within an uncertainty of a few tens of keV, significantly deviates from the experimental mass value and the other theoretical predictions by approximately 2 MeV. Such a significant departure is peculiar and indicates that the masses of the
$ A = 54 $ isospin septet need to be meticulously re-assessed.Although the masses of only four members of the isospin septet are known, it is sufficient to test the quadratic form of the IMME. First, the
$ \chi^2 $ /$ \nu=49 $ is obtained from the quadratic fit to the four mass data using Eq. (1), thus indicating that the quadratic form of IMME is unsuitable to describe the data. The fit residual is presented in Fig. 2. However, the cubic fit yields a d coefficient of 18.6(27), which significantly deviates from zero by more than$ 6.9\sigma $ , thereby indicating a serious breakdown of the quadratic of IMME in the$ A = 54, T = 3 $ isospin septet. The fitted coefficients using both the quadratic and cubic forms of IMME are presented in Table 2.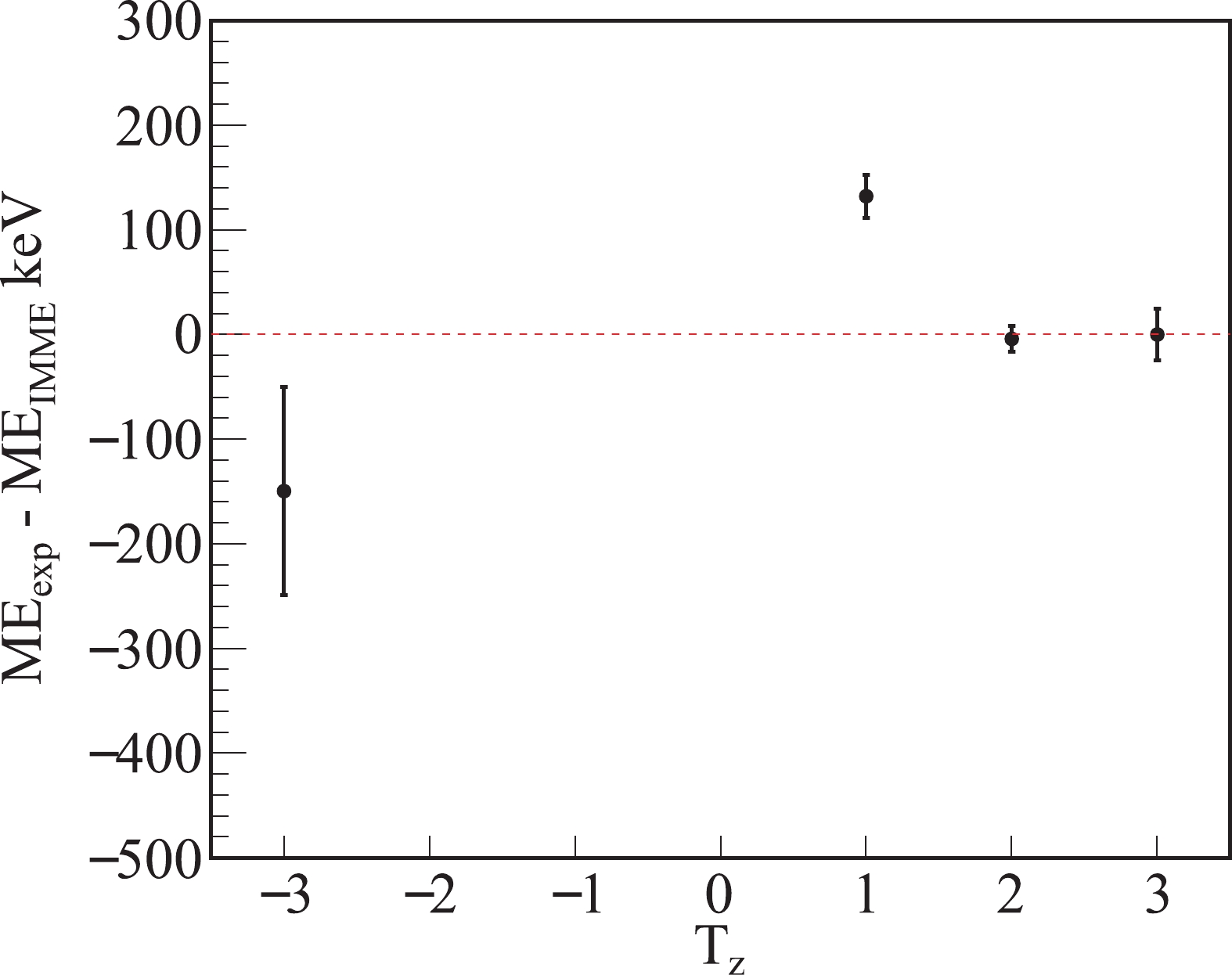
Figure 2. (color online) Fit residuals using the quadratic IMME of Eq. (1) for the A = 54, T = 3 isospin septet.
As aforementioned, the summed effect of all ingredients that break down the quadratic form of IMME will result in a small d value at a level of few keVs. For comparison, d coefficients for all isospin multiplets with A ≥ 16 and T ≥ 3/2, of which ME values of more than three members are known experimentally, are calculated using the cubic form of the IMME. The corresponding ME values of IASs are taken from recent evaluation NUBASE2020 [19]. As can be observed in Fig. 3, almost all d coefficients are compatible with zero within
$ 3\sigma $ . The significant breakdowns of the quadratic IMME are observed for the$ A = 32 $ isospin quintuplet and$ A = 35 $ isospin quartet with$ \left|d\right|/\sigma $ bigger than 8. However, the absolute values of the d coefficients of these two multiplets are less than 4 keV. The case of the$ A = 44 $ isospin quintuplet with the third biggest d value of 10.8(19) was pointed out and discussed comprehensively in Ref. [22]. In that study, it was inferred that "The large d and e coefficients demonstrated in Fig. 9, the so-called breakdown of the IMME, are caused most probably by the mis-identification of the IAS in 44V". If the$ T = 2 $ IAS in the 44V proposed in that work was adopted, the d coefficient of the$ A = 44 $ isospin quintuplet would be –0.7(2.4).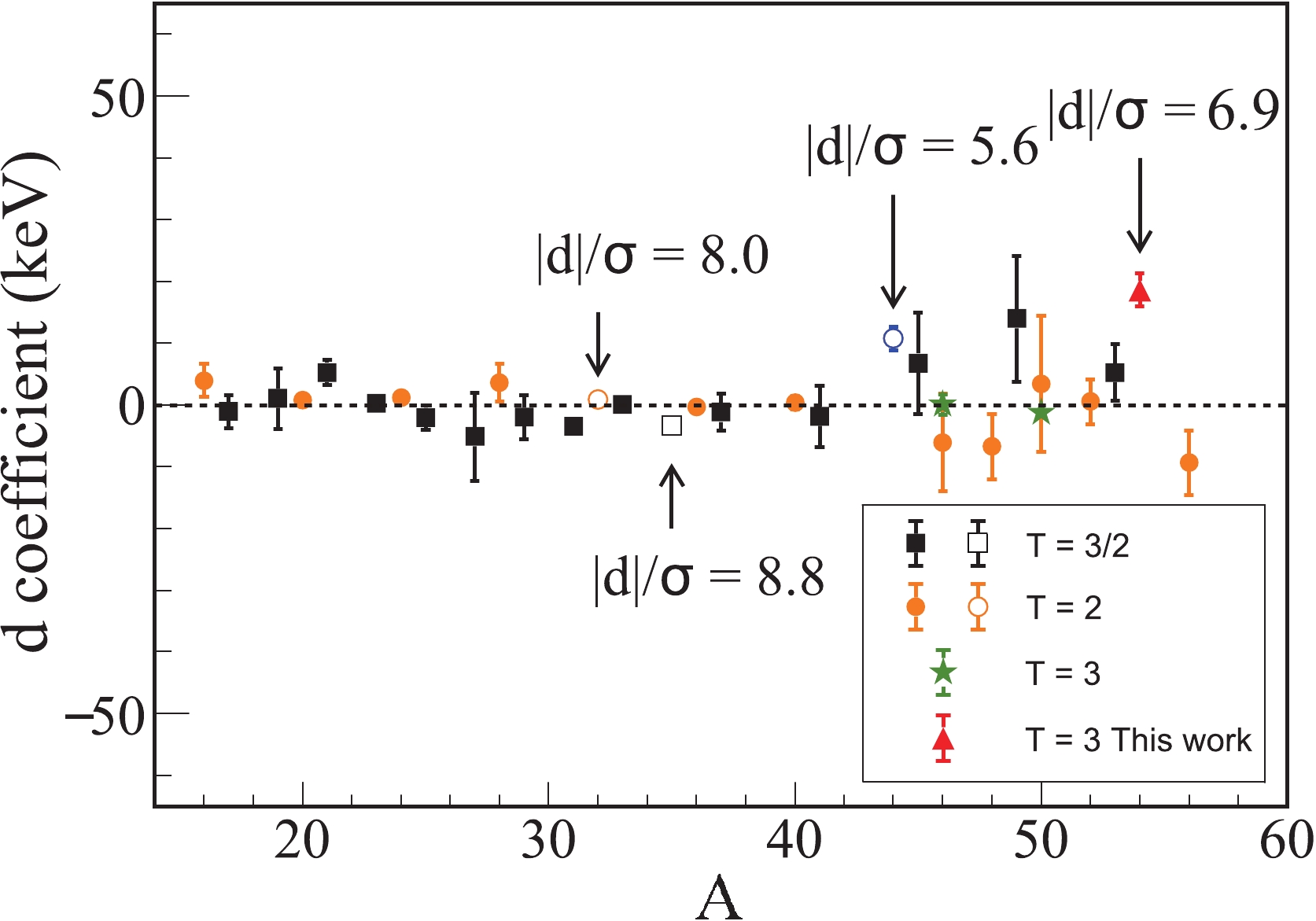
Figure 3. (color online) d coefficients of cubic fit of the IMME for all isospin multiple with A ≥ 16 and T ≥ 3/2. The solid squares, dots and stars represent the d coefficients of isospin multiplets with T = 3/2, T = 2, and T = 3, respectively. The red triangle, represents the d coefficient of the A = 54, T = 3 isospin septet, while the blue open dot represents the one of the A = 44, T = 2 isospin quintuplet. All isospin multiplets with
$\left|d\right|/\sigma$ bigger than 3 are marked.In fact, there were several cases in which the breakdowns of the quadratic form of IMME were first reported; however, it was later discovered that the breakdowns were caused by the mis-assignment of one of the IASs. For example, the new mass of 53Ni [29], together with the other three IASs in the
$ A = 53 $ ,$ T = 3/2 $ isospin quartet, yields a d coefficient of 39 (10 keV), which was too large to be understood by the large-scale shell model calculations [29]. In a later experiment on the β decay of 53Ni, the$ T = 3/2 $ IAS in 53Co was correctly assigned and thus yielded$ d=5.4(46) $ compatible with zero. Another similar case is the$ A = 52 $ isospin quintuplet reported in Ref. [30]. The surprisingly large d coefficient in the present$ A = 54 $ isospin septet may be owing to the mis-assignment of one of the four IASs.We adopt the method introduced by J. Jäneke in Ref. [31]. Assuming that a nucleus can be regarded as a uniformly charged sphere [32], the total Coulomb energy
$E_{\rm C}$ , which breaks the degeneracy of IASs and results in an energy shift between IASs of an isospin multiplet, can be defined as$\begin{aligned}[b] E_{\rm C} =& \frac{3e^2}{5R_{\rm C}}Z(Z-1)\\ = &\frac{3e^2}{5r_{0}A^{1/3}}\left[\frac{A}{4}(A-2)+(1-A)T_z+T^2_{z}\right], \end{aligned} $

(3) where e represents the elementary charge, and
$R_{\rm C} = r_{0}A^{1/3}$ denotes the radius of the nucleus. The coefficients of IMME can be expressed as$ a = \frac{3e^2}{20r_0}\frac{A(A-2)}{A^{1/3}}, $

(4) $ b = -\frac{3e^2}{5r_0}\frac{A-1}{A^{1/3}} +\Delta M_{nH}, $

(5) $ c = \frac{3e^2}{5r_0}\frac{1}{A^{1/3}}, $

(6) where
$ \Delta M_{nH} $ is the mass difference between the neutron and hydrogen. From this simple model, the ratio of the b and c coefficients$ \left|b/c\right| $ is nearly a linear function of$ (A-1) $ .Figure 4 illustrates the dependence of the extracted
$ \left|b/c\right| $ ratios on the corresponding$ A-1 $ for all isospin multiplets with A$ \geqslant $ 16 and T$ \geqslant $ $ 3/2 $ . The b and c coefficients of the isospin multiplets are re-extracted from fits of the quadratic form of the IMME. Similar to the method introduced in Ref. [6], a linear function of$ \left|b/c\right| = p_0 (A - 1) + $ $ p_1 $ is adopted to fit the data. The fitted parameters agree well with those obtained in Ref. [6]. From Fig. 4, it can be observed that the$ \left|b/c\right| $ versus$ A-1 $ shows a good systematics, which can be well described by the linear function.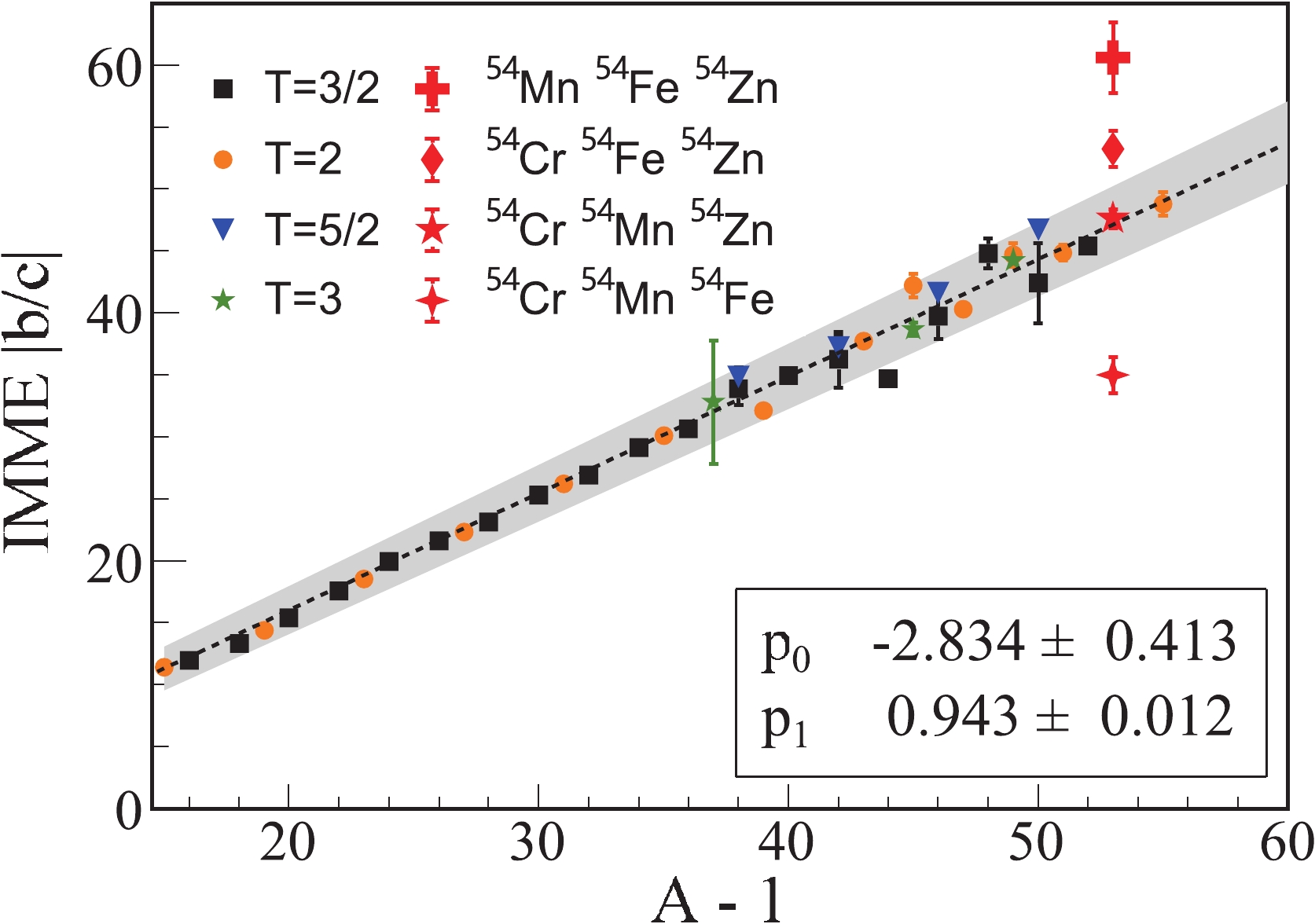
Figure 4. (color online) Dependence of the quantity
$|b/c|$ on A – 1 for all isospin multiplets. The four red symbols represent results from A = 54, T = 3 isospin multiplets. The gray shading area represents the$3\sigma$ error band of the fitted linear function.For the
$ A=54 $ ,$ T=3 $ isospin multiplet, four combinations of three IASs are adopted to extract the a, b, and c coefficients of the quadratic IMME, and the$ \left|b/c\right| $ ratios are obtained and illustrated in Fig. 4. It is found that once the$ T=3 $ IAS in 54Fe is used in the analysis, the extracted$ \left|b/c\right| $ values are beyond the$ 3\sigma $ error band of the fit function. Only if the$ T=3 $ IAS in 54Fe is excluded, the$ \left|b/c\right| $ value fits well into the general trend of the systematics. This indicates that the breakdown of the IMME at$ A = 54 $ ,$ T=3 $ isospin multiplet may be caused by the mass of the$ T = 3 $ IAS in 54Fe.If we intentionally make the d coefficient approach zero or make the
$ \left|b/c\right| $ values to be in line with the general trend, the excitation energy of the$ T = 3 $ IAS in 54Fe would have to be reduced by 150 keV. In fact, a state with an excitation energy of 14730 keV, 140 keV lower than the IAS of 14870 keV, was observed in Ref. [33]. Referring to the aforementioned cases [22, 30, 34], the first possibility that would trigger the breakdown of IMME would be the mis-assignment of the$ T = 3 $ IAS in 54Fe. However, the mass of the$ T = 3 $ IAS in 54Fe was determined using the 52Cr(3He, n)54Fe transfer reaction [33]. In these reactions, the spin and parity assignments for populated states were determined based on the distorted-wave calculations for angular distributions of reaction products, i.e., protons or neutrons. This approach is a long-standing method widely used in data analysis of transfer reaction experiments from 1960s. It remains uncertain to attribute such breakdown of IMME to the mis-assignment of the IAS in 54Fe. Hence, a new transfer reaction experiment with a higher resolution is highly desirable to address the issue.An alternative scenario that may explain the breakdown of IMME is the isospin mixing between the IAS and close-lying states of the same spin-and-parity,
$ J^{\pi} $ , but with different isospins. In fact, the level density is generally very high at the excitation of approximately 15 MeV; hence, it is not unusual to have such states of the same$ J^{\pi} $ as that of the IAS. It is well-known that the unperturbed IAS would be shifted up or down owing to the isospin mixing. The energy shift depends on the matrix element of isospin non-conserving Hamiltonian ($ V_{\rm{INC}} $ ), and it may be enhanced by the proximity of levels involved in the isospin mixing. However, the$ V_{\rm{INC}} $ is usually very small, thereby leading to the energy shift at the order of several tens of keV. This phenomenon has been confirmed in recent experiments on fp-shell nuclei [35–37]. Hence, under the scenario of isospin mixing, the large energy shift of approximately 150 keV for the claimed$ T=3 $ IAS in 54Fe [33] is also quite odd and needs to be further investigated theoretically and experimentally.In summary, the mass of two-proton emitter 54Zn was deduced indirectly thanks to the precise mass measurement of 52Ni. Although the deduced mass value agrees with the predictions from various nuclear mass models, it disagrees with the IMME prediction. A serious breakdown of the IMME at
$ A = 54 $ isospin septet was discovered with the d coefficient being as large as 18.6(27). This anomaly has been analyzed and discussed in this paper. We suggested that two scenarios could be responsible for such an anomaly: one is concerned with the mis-assignment of the$ T = 3 $ isobaric analogue state (IAS) in the$ T_z = 1 $ nucleus 54Fe, and the other could be owing to the extremely strong isospin mixing. To verify and further investigate the breakdown, the direct mass measurement for 54Zn, re-determination for$ T = 3 $ IAS in 54Fe, and measurements for other three still unknown$ T = 3 $ IASs are highly recommended. Considering the short half-life (1.8 ms) of 54Zn, the High Intensity Accelerator Facility [38] coupled with single-ion sensitive isochronous mass spectrometry [39] may be a suitable location to conduct a precise mass measurement for this short-lived and low-production nucleus.
On the masses of A = 54 isospin septet and the isobaric multiplet mass equation
- Received Date: 2022-02-15
- Available Online: 2022-06-15
Abstract: Using the ground-state mass of 52Ni and two-proton decay energy of 54Zn, the ground-state mass excess of 54Zn is deduced to be –6504(85) keV. This value is about 2 MeV lower than the prediction of the quadratic form of the isobaric multiplet mass equation (IMME). A cubic fit to the existing mass data of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: