-
Precise measurements of and predictions for
$ t \bar t $ pair production are crucial for tests of the standard model and for searching for new physics beyond the standard model [1]. Thus, an understanding of the uncertainties resulting from an imperfect knowledge of parton distribution functions (PDFs) is crucial. The large integrated luminosity and the high center-of-mass energy of the Large Hadron Collider (LHC) provide a large sample of$ t \bar t $ events. The dominant production mechanism for$ t\bar t $ pair production at the LHC is through gluon-gluon fusion; thus,$ t\bar t $ data have the potential to constrain the gluon PDF, especially at high x. In the analysis carried out in Ref. [2], theoretical predictions for the final-state top quark$ p_T^t $ and$ y_t $ distributions in$ t \bar t $ pair production at the LHC at approximate next-to-next-to-leading order (aNNLO) in QCD are used to study the impact of ATLAS and CMS 7 TeV differential cross section measurements on proton PDFs. The aNNLO theory prediction in [2] uses methods of QCD threshold resummation beyond the leading logarithmic accuracy and is implemented in the xFitter platform [3] using fastNLO tables to facilitate the global PDF analysis. A moderate improvement in the uncertainty of the gluon distribution at high x was observed. More recent analyses in Refs. [4, 5] have also provided fastNLO tables for the exact NNLO predictions of the invariant mass of the top-quark pair, the average transverse momentum of the$ t,\bar{t} $ quark, the average rapidity of the$ t,\bar{t} $ quark, and the rapidity of the top-quark pair, i.e., the distributions measured by the ATLAS and CMS experiments. The fastNLO tables are at NNLO in QCD with$ m_t = 173.3 $ GeV, renormalization scale and factorization scales$ \mu_R = \mu_F = H_T/4 $ ,$ H_T = \sqrt {m^2_t + p^2_{T,t}} + \sqrt {m^2_t + p^2_{T,\bar t}} $ for$ m_{t\bar t} $ ,$ y_{t\bar t} $ , and$ y_t $ distributions, and$\mu_R = \mu_F = m_T/ 4 = \dfrac{1}{4}\sqrt {m^2_t + p^2_{T}}$ for the$ p_{T} $ distribution of the average top/antitop quark. In their calculation, they use the same binning (see Table 1) as the ATLAS [6] and CMS [7] 8 TeV measurements of top-quark pair differential cross-sections.Observable Binning $ \mu_{\rm{F}}=\mu_{\rm{R}} $ 

${\rm d}\sigma/{\rm d}m_{t\bar{t} }/{\rm{GeV} }$ 

$ \{345,\,400,\,470,\,550,\,650,\,800,\,1100,\,1600\} $ 

$ H_T/4 $ 

${\rm d}\sigma/{\rm d}y_t$ 

$ \{-2.5,\,-1.6,\,-1.2,\,-0.8,\,-0.4,\,0.0,\,0.4,\,0.8,\,1.2,\,1.6,\,2.5 \} $ 

$ H_T/4 $ 

${\rm d}\sigma/{\rm d}y_{t\bar{t} }$ 

$ \{-2.5,\,-1.3,\,-0.9,\,-0.6,\,-0.3,\,0.0,\,0.3,\,0.6,\,0.9,\,1.3,\,2.5 \} $ 

$ H_T/4 $ 

${\rm d}\sigma/{\rm d}p^t_T /{\rm{GeV} }$ 

$ \{0,\, 60,\, 100,\, 150,\, 200,\, 260,\, 320,\, 400,\, 500\} $ 

$ m_T/2 $ 

Table 1. Summary of the fastNLO tables provided in Ref. [5].
In this paper, we study the impact of the ATLAS [6] and CMS [7] measurements of top-quark pair differential cross-sections data on the CT14HERA2 [8] and CT14HERA2mJ PDFs; thus, in Table 2, we provide the relevant basic information. For the measurements in Table 2, the ATLAS experiment has provided statistical errors, with fifty six correlated systematic errors, including luminosity errors. CMS collaboration provided the statistical errors, along with eleven correlated systematic errors, including the luminosity errors.
Detector Observable $ N_{pts} $ 

$ \chi^2/N_{pts} $ (CT14HERA2)

$ \chi^2/N_{pts} $ (CT14HERA2mJ)

weight=1.0 weight=9.0 CDF inclusive jet [9] 72 1.46 − 1.50 D0 inclusive jet [10] 110 1.03 − 1.03 ATLAS inclusive jet [11] 90 0.57 − 0.57 CMS inclusive jet [12] 133 0.89 − 0.93 ATLAS $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}|y_{t\bar t}|}, \dfrac{{\rm d}\sigma}{{\rm d}|y_{t\bar t|} } $ [6]

5 2.21, 3.83 1.18, 1.48 5.21, 7.29 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}m_{t\bar t} }, \dfrac{{\rm d}\sigma}{{\rm d}m_{t\bar t} } $ [6]

7 0.25, 0.45 0.25, 0.42 0.35, 0.40 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}|y_t|}, \dfrac{{\rm d}\sigma}{{\rm d}|y_t|} $ [6]

5 2.40, 2.83 1.45, 1.62 5.34, 5.79 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}p^t_T}, \dfrac{{\rm d}\sigma}{{\rm d}p^t_T} $ [6]

8 0.39, 0.34 0.38, 0.33 0.38, 0.32 CMS $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}y_{t\bar t} } $ [7]

10 2.31 1.07 3.34 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}m_{t\bar t} } $ [7]

7 7.69 3.96 9.30 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}y_t} $ [7]

10 2.52 2.50 3.32 $\dfrac{1}{\sigma} \dfrac{{\rm d}\sigma}{{\rm d}p^t_T} $ [7]

8 3.55 2.20 4.82 Table 2. Number of data points and
$ \chi^2/N_{pts} $ for inclusive jet and top-quark pair data, after ePump updating from the CT14HERA2 and CT14HERA2mJ PDFs.In Table 2, we provide the number of data points and
$ \chi^2/N_{pts} $ for inclusive jet and top-quark pair data, after updating using ePump from the CT14HERA2 and CT14HERA2mJ PDFs. For the top-quark pair data, the$ \chi^2/N_{pts} $ decreases for CT14HERA2 rather than for CT14HERA2mJ PDFs. This shows that the quality of the original CT14HERA2mJ PDFs is enhanced after including inclusive jet data. However, this is not the case for the ATLAS absolute and normalized$ p^t_T $ , as well as the absolute$ m_{t\bar t} $ distributions;$ \chi^2 $ also did not decrease visibly in these distributions, even when we set the weight = 9. The$ \chi^2/N_{pts} $ of the four inclusive jet distributions are very different from those of the top-quark distributions.$ \chi^2/N_{pts} $ is considerably larger in CMS normalized$ t\bar t $ distributions than in ATLAS normalized$ t\bar t $ distributions. This result means that, at the least, there are some comparable differences between CMS and ATLAS data for the same measurements while using the same theoretical predictions.Refs. [13, 14] have previously studied the impact of top-quark pair differential distributions measured by ATLAS [6] and CMS [7] at 8 TeV on the gluon PDF within the NNPDF framework. They found that the differential distributions from top-quark pair production provide relatively strong constraints on the large-x gluon. Within the MMHT framework, Ref. [15] found that the impact of the ATLAS [6] data on the gluon PDF is relatively weak. With the CMS data [7], they found that both
$ y_t $ and$ y_{t\bar t} $ distributions have a noticeable impact on the gluon PDF at high x, where the impact of$ y_{t\bar t} $ is greater than that of$ y_t $ . This paper examines in detail the impact of the LHC$ t \bar{t} $ data in the CTEQ-TEA framework.Despite improvements, such as the use of fastNLO tables, global PDF fitting is still very CPU-intensive. In Ref. [16], a software package, called the error PDF Updating Method Package (ePump) [16], was developed, which can provide both the updated best-fit PDF and the updated eigenvector PDFs from a PDF set previously obtained by a global PDF analysis. ePump has been previously used [17-20] to perform analyses that have the potential to reduce PDF uncertainties at the LHC.
In this paper, we use ePump to study the impact of the LHC 8 TeV single differential top-quark pair distribution data from ATLAS [6] and CMS [7] on the gluon PDFs, starting from the global PDF sets CT14HERA2 [8] and CT14HERA2mJ. CT14HERA2 is an updated version of the CT14NNLO PDFs [21], with the HERA Run I data replaced by the combined HERA I+II data [22]. The CT14HERA2 PDF fit contains inclusive jet data from the Tevatron and from the LHC. Because inclusive jet data also provide constraints on the gluon distribution, additional PDFs, called CT14HERA2mJ, were constructed by a full PDF global analysis, without the jet data, to examine more closely the impact of the
$ t \bar{t} $ data alone and in combination with the jet data.The absolute and normalized (to the total
$ t \bar{t} $ cross section) single differential$ t\bar t $ measurements from ATLAS in the variables$ |y_{t\bar t}| $ ,$ {\rm d}m_{t\bar t} $ ,$ p^t_T $ , and$ |y_t| $ and the normalized single differential$ t\bar t $ measurements from CMS in the variables$ y_{t\bar t} $ ,$ m_{t\bar t} $ ,$ p^t_T $ , and$ y_t $ are listed in Table 2. We also show the number of data points for jet data that are included in the CT14HERA2 fit. The values of$ \chi^2/N_{pts} $ in the Table 2 are calculated using ePump to update the CT14HERA2 and CT14HERA2mJ PDFs with the inclusion of each individual$ t\bar t $ data set. These will be discussed in detail later in this paper.This paper is organized as follows. In section II, we first calculate the degree of correlation between the CT14HERA2 gluon PDF and the ATLAS and CMS 8 TeV
$ t \bar{t} $ data. Then, we compare the ePump updated gluon PDFs obtained by adding those data one by one, to the original CT14HERA2 PDFs. The corresponding NNLO theory for$ t \bar{t} $ predictions using the updated PDFs is then compared with the corresponding ATLAS and CMS measurements. The impact of the updated PDFs on the Higgs boson gluon-gluon fusion cross section$ \sigma_H (gg \rightarrow H) $ is then discussed. In section III, tensions between the ATLAS and CMS 8 TeV absolute and normalized single differential$ t\bar t $ data with the other data sets in the CT14HERA2 PDFs are described. In section IV, using the same method utilized with the CT14HERA2 PDFs, we analyze the impact of the ATLAS and CMS 8 TeV single differential$ t\bar t $ measurements on the CT14HERA2mJ PDFs. In section V, we compare the impact from the CMS 7 TeV inclusive jet data and from the$ t \bar{t} $ data. In section VI, the impact of the value of the top quark mass on the single differential$ t \bar{t} $ cross section predictions is analyzed. Our conclusions are presented in section VII.Before beginning the full discussion of the analysis, we summarize the notations used in this paper:
● The suffix “.54” in CT14HERA2.54 indicates that the error band is obtained with 54 eigen-vector PDF sets, rather than with the entirety of the 56 PDF sets. The last two sets are omitted, which expands the uncertainty for the small x gluon, a region not relevant for this study.
● CT14HERA2mJ PDFs are obtained after excluding the four jet data sets present in the CT14HERA2 PDFs.
● The ePump updated CT14HERA2.54 (CT14HERA2mJ) PDFs using the ATLAS 8 TeV absolute and normalized data in the
$ |y_{t\bar t}| $ ,$ m_{t\bar t} $ ,$ |y_t| $ , and$ p^t_T $ distributions are denoted using suffixes XXX and NXXX attached to the absolute and normalized distributions, respectively. -
In this section, we examine the impact of the ATLAS [6] and CMS [7] 8 TeV
$ t\bar{t} $ data in the CT14HERA2.54 global PDF fit and fastNLO theory at NNLO in QCD [4, 5]. The integrated luminosities of the ATLAS and CMS 8 TeV measurements are 20.3 fb−1 [6] and 19.7 fb−1, respectively. -
The correlation between a specific absolute or normalized
$ t\bar t $ data point and$ g(x, Q ) $ gluon PDF at a given x and Q value is represented by the correlation cosine$ \cos\phi $ [23, 24]. Here, the quantity of$ \cos\phi $ characterizes whether the data point and the PDF are correlated ($ \cos\phi \sim 1 $ ), anti-correlated ($ \cos\phi \sim -1 $ ), or uncorrelated ($ \cos\phi \sim 0 $ ). Large positive and negative values of$ \cos\phi $ indicate direct sensitivity of the$ t\bar t $ data point to the gluon PDF in a particular region in x. In Fig. 1, the correlation coefficient between the CT14HERA2.54 g($ x, Q = 100 $ GeV) PDF and the absolute (left) and normalized (right) differential$ t\bar t $ data is distinguished by varying the type of line used. Each data point is represented by its own correlation curve. Solid green lines, magenta dotted lines, red dashed lines, and dark blue long-dashed-dotted lines correspond to the LHC 8 TeV absolute (left) and normalized (right) differential$ t \bar t $ cross-section data as a function of$ |y_{t\bar t}| $ ,$ m_{t\bar t} $ ,$ |y_t| $ , and$ p^t_{T} $ , respectively. We observe that, because of the kinematic range, the absolute$ t \bar{t} $ distributions are highly correlated with the gluon PDF for$ 0.08 \lesssim x \lesssim 0.4 $ and highly anti-correlated for$ 10^{-4} \lesssim x \lesssim 10^{-2} $ . We also observe that, because of the total$ t \bar{t} $ pair production in the denominator, the normalized$ t \bar{t} $ distributions show correlations that are basically the same for each variable and are a mirror image of the dominant behavior of the$ \cos\phi $ distributions for the absolute data.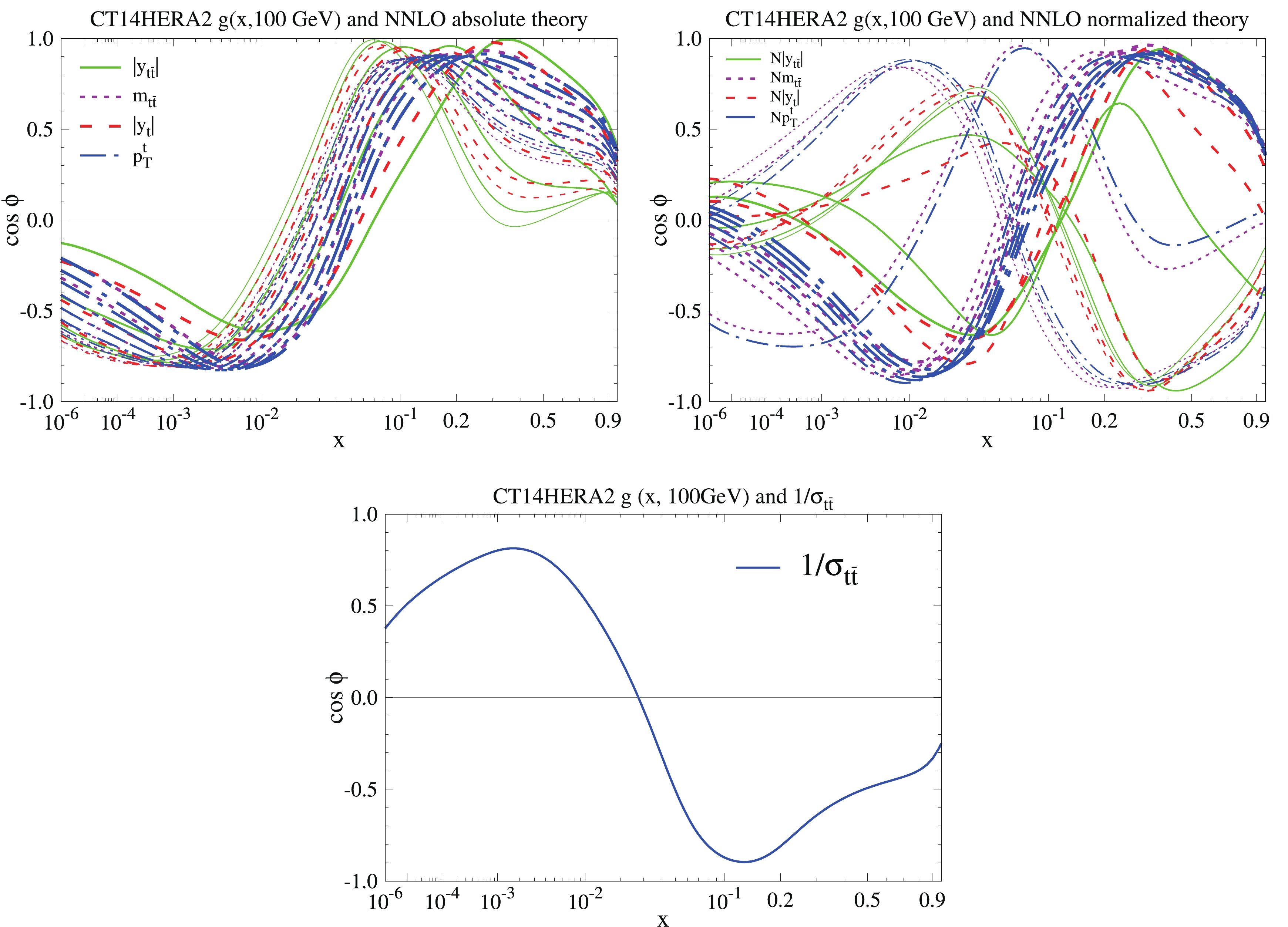
Figure 1. (color online) Correlation cosine
$ \cos \phi $ between the CT14HERA2.54$g(x,Q = 100\;{\rm GeV})$ PDF and fastNLO predictions for each bin of the$ t\bar t $ differential distribution absolute (left) and normalized (right), as well as inverse of the total cross sections (bottom). Note that the thickness of the line for each distribution changes from thin to thick, which corresponds to moving from the first bin to the last bin. -
In this section, using the CT14HERA2.54 PDFs as a basis, we study the impact of the the ATLAS (absolute and normalized) and CMS (normalized) 8 TeV
$ t\bar t $ full phase-space differential cross-sections as a function of the$ y_{t\bar t} $ ,$ m_{t\bar t} $ ,$ p^t_T $ , and$ y_t $ variables on the gluon PDF. The ATLAS and CMS$ t\bar{t} $ data are included individually using ePump. The results are shown in Fig. 2. The impact on both the central gluon distribution and on the gluon uncertainty band (with respect to the CT14HERA2.54 gluon PDF) is shown. It is evident that there is no notable impact on the central gluon from either the absolute or normalized ATLAS 8 TeV$ t\bar{t} $ data for the$ m_{t\bar t} $ and$ p^t_T $ distributions. However, both the absolute and normalized$ |y_{t\bar t}| $ and$ |y_t| $ distributions have a relatively minor impact on the best fit gluon PDF$ x > 0.2 $ . It is also evident that none of the distributions result in a significant reduction of the gluon PDF uncertainty at any x value. This implies that the ATLAS$ t\bar{t} $ single differential data are in strong tension with the other data included in CT14HERA2, the gluon PDF is well constrained by other data, or both. In contrast to the ATLAS data, we observe that the CMS normalized$ y_{t\bar t} $ ,$ m_{t\bar t} $ , and$ p^t_{T} $ data provide relatively larger impacts on both the central predictions and the uncertainty bands of the CT14HERA2.54 gluon PDF at high x, while the$ y_t $ distribution does not. In the region$ x>0.1 $ , the inclusion of the$ y_{t\bar t} $ ,$ m_{t\bar t} $ , and$ p^t_{T} $ data leads to a decrease in the gluon PDF, but it is still well within the PDF error band. It is known that, in general, the gluon PDF is primarily constrained by the DIS and jet data. -
In this section, we apply the ePump optimization method to further explore the impact of the ATLAS and CMS 8 TeV
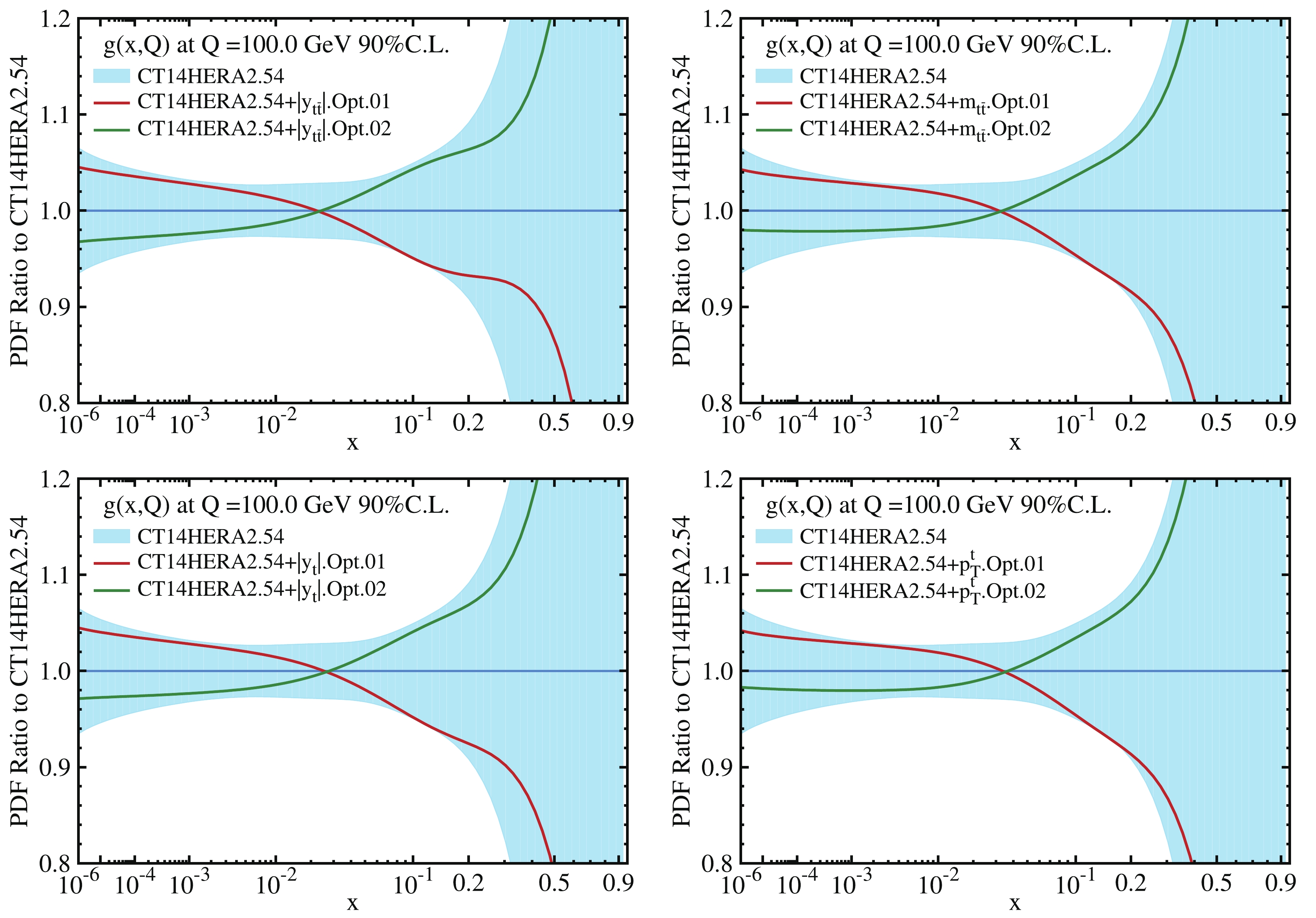
$ t\bar t $ differential cross section data on the gluon PDF uncertainty. The ePump optimization method is similar to the data set diagonalization method [25]. For the optimization, we use CT14HERA2.54 error PDFs that have 27 error set pairs, the absolute and normalized 8 TeV$ t\bar t $ differential cross sections from NNLO$ t\bar t $ fastNLO tables [4, 5]. The optimized error PDFs are ordered by the size of their eigenvalues, and one can determine how many error PDFs are necessary to obtain the dependence of the observables on the PDFs. The sensitivity of each$ t\bar t $ data point to the gluon PDF in the relevant x-range can be illustrated by comparing the pair of gluon error PDFs (two for each eigenvector) with the original CT14HERA2 gluon error PDFs, relative to the CT14HERA2 best fit values. Therefore, in Figs. 3 and 4, we have plotted ratios of the first pair of gluon error PDFs (red and green lines) and the original CT14HERA2.54 gluon error PDFs (blue band) at$ Q = 100 $ GeV to the CT14HERA2 best fit value of the gluon PDF. In addition, in Table 3, we provide the maximal amount of gluon error bands covered by the first and second eigenvector pairs for four$ t\bar t $ differential distributions. From this table, we see that the first and second eigenvector pairs of gluon error PDFs almost completely cover the CT14HERA2.54 gluon PDF error bands for the whole x-range, indicating the dependence of the$ t\bar t $ differential cross section on the gluon PDF. Because the other eigenvector pairs, after ePump-Optimization, have a negligible effect, the total error band of the gluon PDF, in the relevant x-region, can be approximated by taking the quadrature sum of the error bands from the first two leading eigenvector sets. The contribution from the remaining 23 eigenvectors pairs is almost identically zero. The first eigenvector pair gives the largest contribution to the PDF uncertainty for each$ t\bar t $ distribution; in particular, it is greater than 90% for absolute$ m_{t\bar t} $ and$ p^t_T $ as well as normalized$ |y_t| $ distributions. Because the PDF uncertainty for each$ t\bar t $ distribution depends mostly on the first and second eigenvector pairs, we may use only these four eigenvector PDFs to study the PDF-induced uncertainty related to the$ t\bar t $ production, instead of using the full 54 error sets of CT14HERA2+$ t\bar t $ PDFs.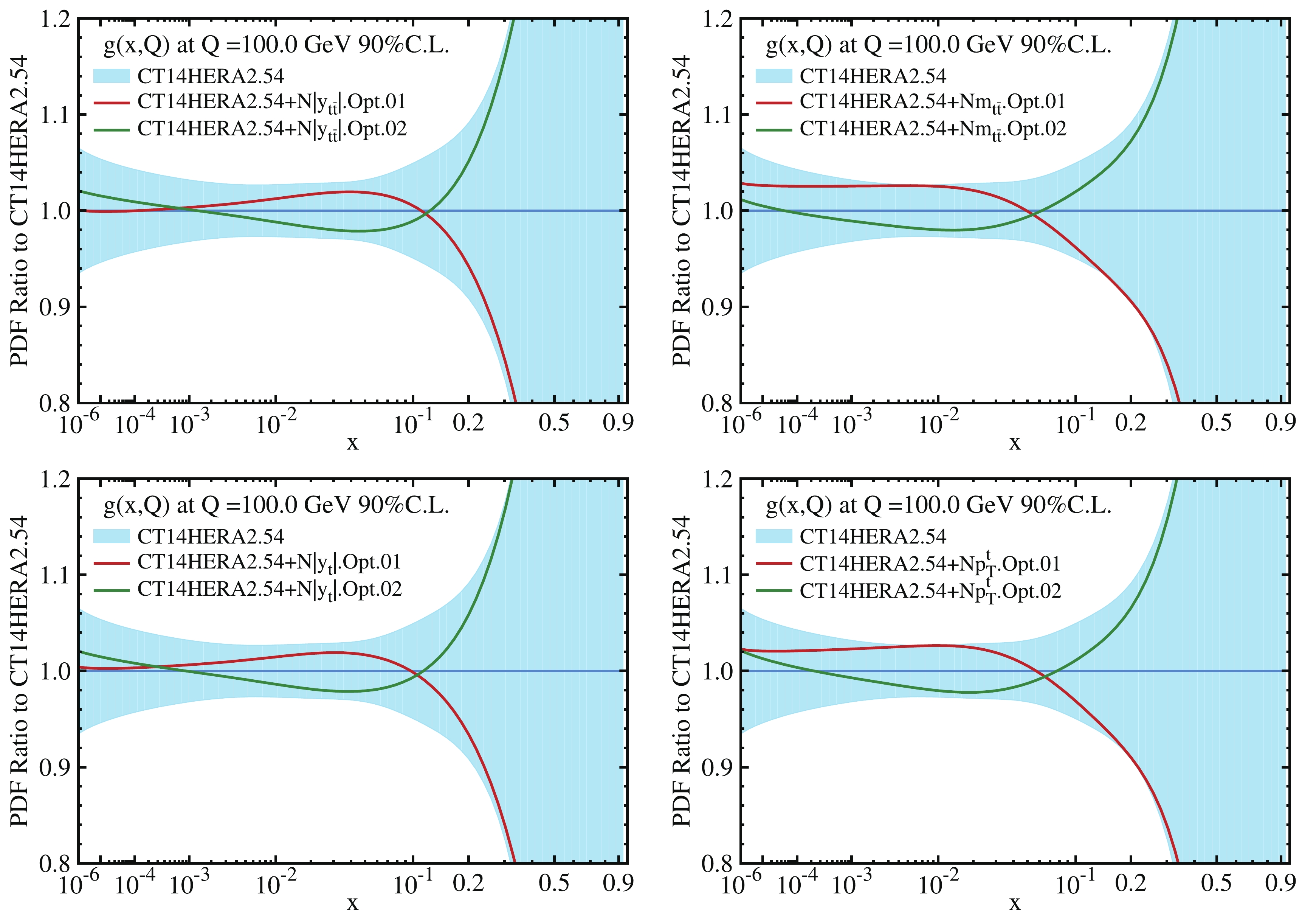
Figure 3. (color online) Ratio of the first pair of updated error PDFs and original CT14HERA2.54 error PDFs to the CT14HERA2 central value of gluon PDF at
$ Q = 100 $ GeV.distributions first eig.vec. normalized (%) absolute (%) second eig.vec. normalized (%) absolute (%) $ y_{t\bar t} $ 

(01,02) 82.4 71.9 (03,04) 17.4 25.6 $ m_{t\bar t} $ 

84.1 92.5 15.8 7.3 $ y_t $ 

90.6 83.5 9.2 16.0 $ p^t_T $ 

86.1 93.2 13.7 6.7 Table 3. Eigenvalues of the first and second eigenvector pairs.
-
In this subsection, we show the theoretical predictions after considering the
$ t\bar t $ data and compare them with the experimental measurements. The comparisons between the theoretical predictions from before and after updating the CT14HERA2.54 PDFs and the ATLAS 8 TeV absolute and normalized differential$ t \bar t $ data, as well as CMS 8 TeV normalized differential$ t \bar t $ data, are presented in Figs. 5, 6, and 7. In these figures, the magenta solid lines correspond to the theoretical predictions from CT14HERA2.54, and the blue solid lines are the theoretical predictions from updated CT14HERA2.54 PDFs. The black and red error bars for each data point and shifted data point (upper part of the figure) include only statistical error. Shifted data$ D_k^{sh} $ is defined as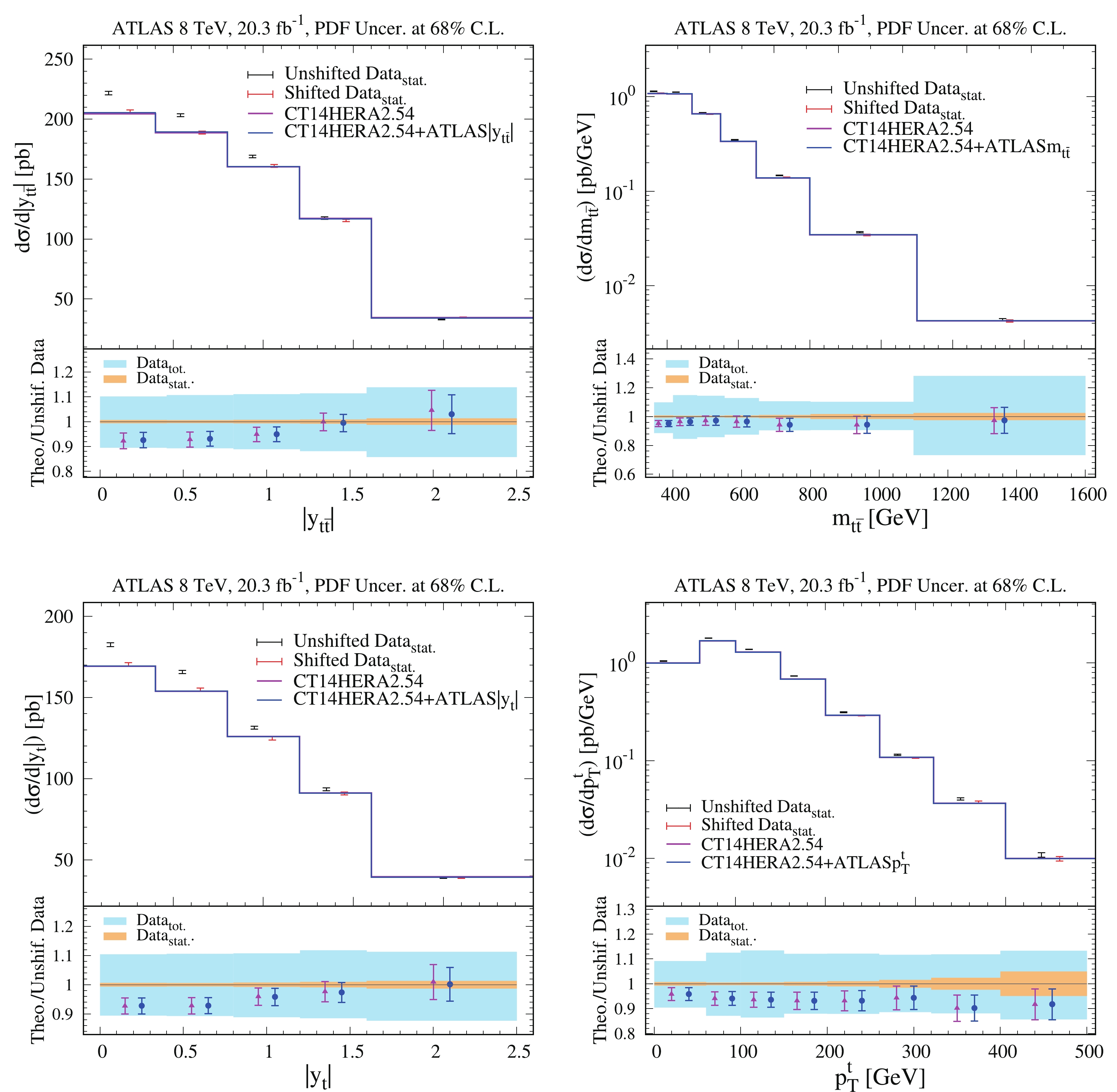
Figure 5. (color online) Comparison of differential cross sections
${\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,${\rm d}\sigma/{\rm d}m_{t\bar t}$ ,${\rm d}\sigma/{\rm d}|y_t|$ , and${\rm d}\sigma/{\rm d}p^t_T$ from CT14HERA2.54 PDFs and from ePump updated CT14HERA2.54+ATLAS$ |y_{t\bar t}| $ , CT14HERA2.54+ATLAS$ m_{t\bar t} $ , CT14HERA2.54+ATLAS$ |y_t| $ , and CT14HERA2.54+ATLAS$ p^t_T $ PDFs and differential ATLAS 8 TeV$ t\bar t $ production cross section data as functions of$ |y_{t\bar t}| $ ,$ m_{t\bar t} $ ,$ |y_t| $ , and$ p^t_{T} $ .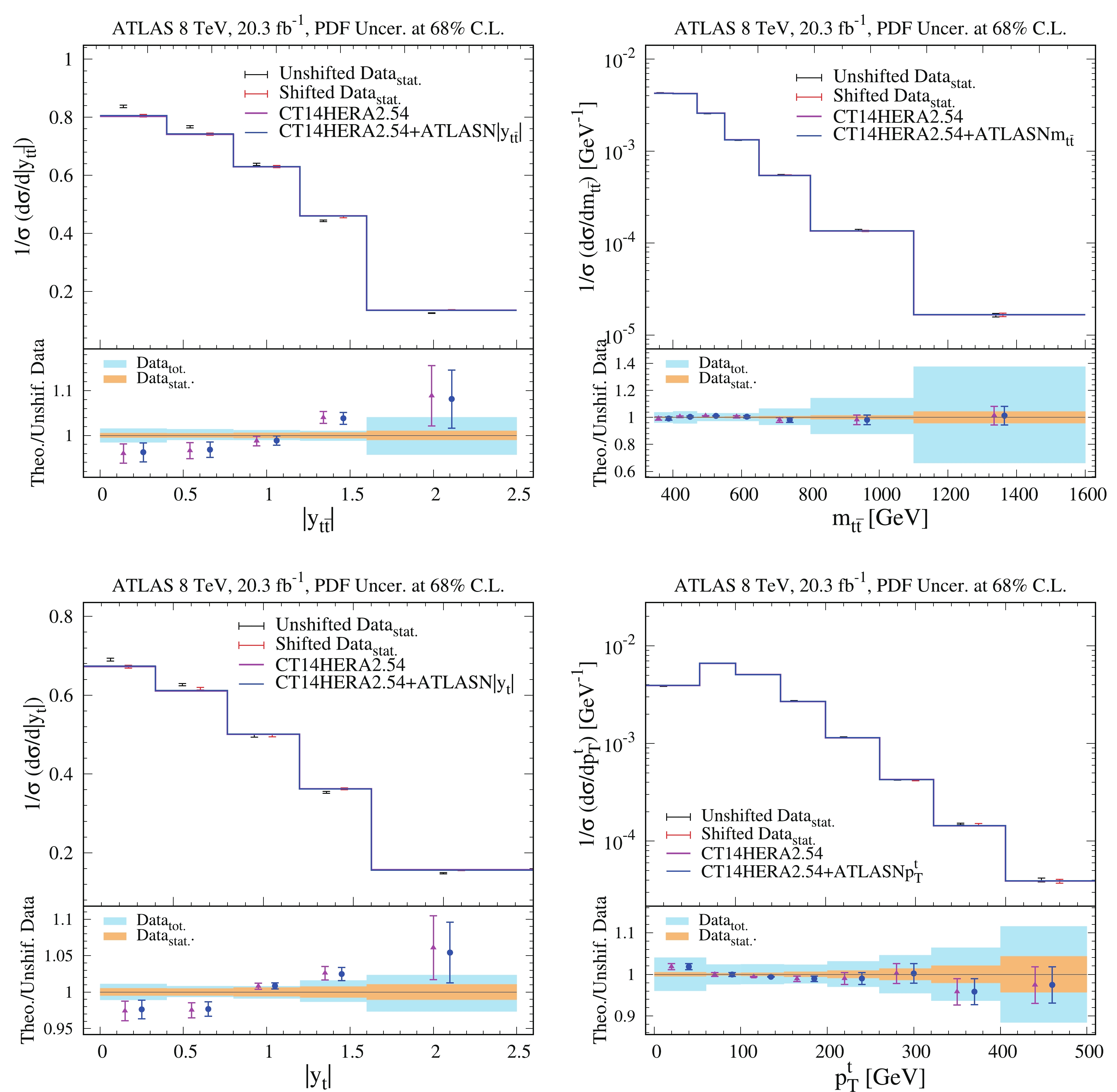
Figure 6. (color online) Comparison of normalized differential cross sections
$1/\sigma \; {\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}p^t_T$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}|y_t|$ from CT14HERA2.54 PDFs and from ePump updated CT14HERA2.54+ATLASN$ |y_{t\bar t}| $ , CT14HERA2.54+ATLASN$ m_{t\bar t} $ , CT14HERA 2.54+ ATLASN$ |y_t| $ , and CT14HERA2.54+ATLASN$ p^t_T $ PDFs and normalized differential ATLAS 8 TeV$ t\bar t $ production cross section data as functions of$ |y_{t\bar t}| $ ,$ m_{t\bar t} $ ,$ |y_t| $ , and$ p^t_{T} $ .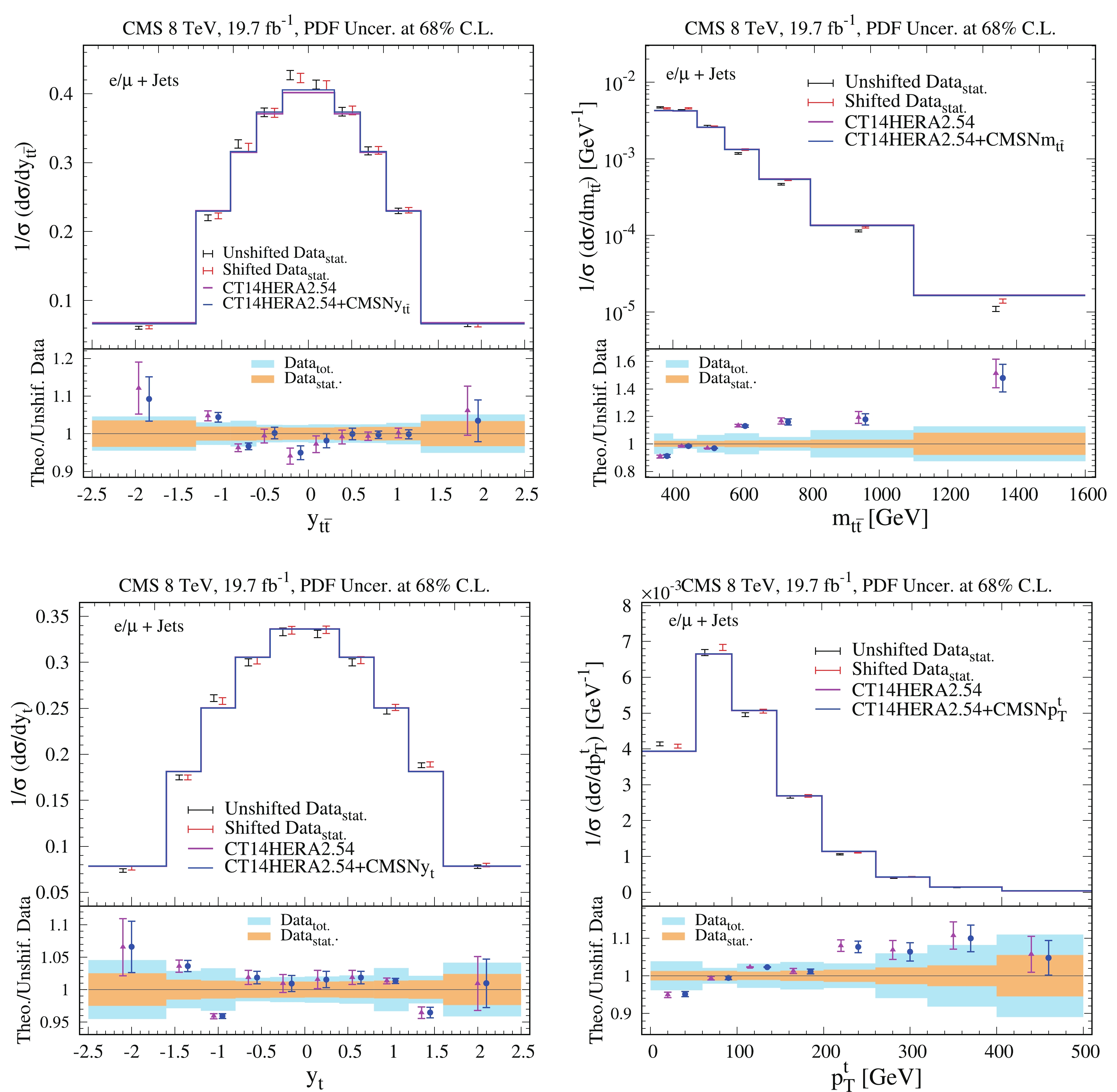
Figure 7. (color online) Comparison of normalized differential cross sections
$1/\sigma \; {\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}p^t_T$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}|y_t|$ from CT14HERA2.54 PDFs and from ePump updated CT14HERA2.54+CMSN$ y_{t\bar t} $ , CT14HERA2.54+CMSN$ m_{t\bar t} $ , CT14HERA2.54+ CMSN$ y_t $ , and CT14HERA2.54+CMSN$ p^t_T $ PDFs and CMS 8 TeV normalized differential$ t\bar t $ production cross section data as functions of$ y_{t\bar t} $ ,$ m_{t\bar t} $ ,$ y_t $ , and$ p^t_{T} $ .$ D_k^{sh}\equiv D_k - \sum\limits_{\alpha = 1}^{N_{\lambda}} \lambda_{\alpha}(a_0) \beta_{k\alpha} , $

where
$ D_k $ is the k-th data point (value),$ \lambda_\alpha $ is known as a nuisance parameter, and$ \sum_{\alpha = 1}^{N_{\lambda}} \beta_{k\alpha} $ are the correlated systematic errors for the k-th data point. The blue bands in the ratio plots indicate the total uncertainty, which is the quadratic sum of statistical and systematic uncorrelated uncertainties, of the data in each bin. The yellow bands in the ratio plots indicate the statistical uncorrelated uncertainties of the data in each bin. The error bars on the theoretical predictions show the 68% C.L. There is an overall shift for all raw data points. This means that the correlated systematic errors, weighted by their corresponding nuisance parameters, play an important role in the fitting. We find that there is little improvement in agreement with the measurements after calculating theoretical predictions evaluated with the new PDFs obtained by adding the ATLAS and CMS 8 TeV$ t\bar t $ production differential cross section data. -
As we showed in the previous two sections, we observe that the CT14HERA2 gluon PDF receives a minor impact after including the 8 TeV ATLAS absolute and normalized and CMS normalized
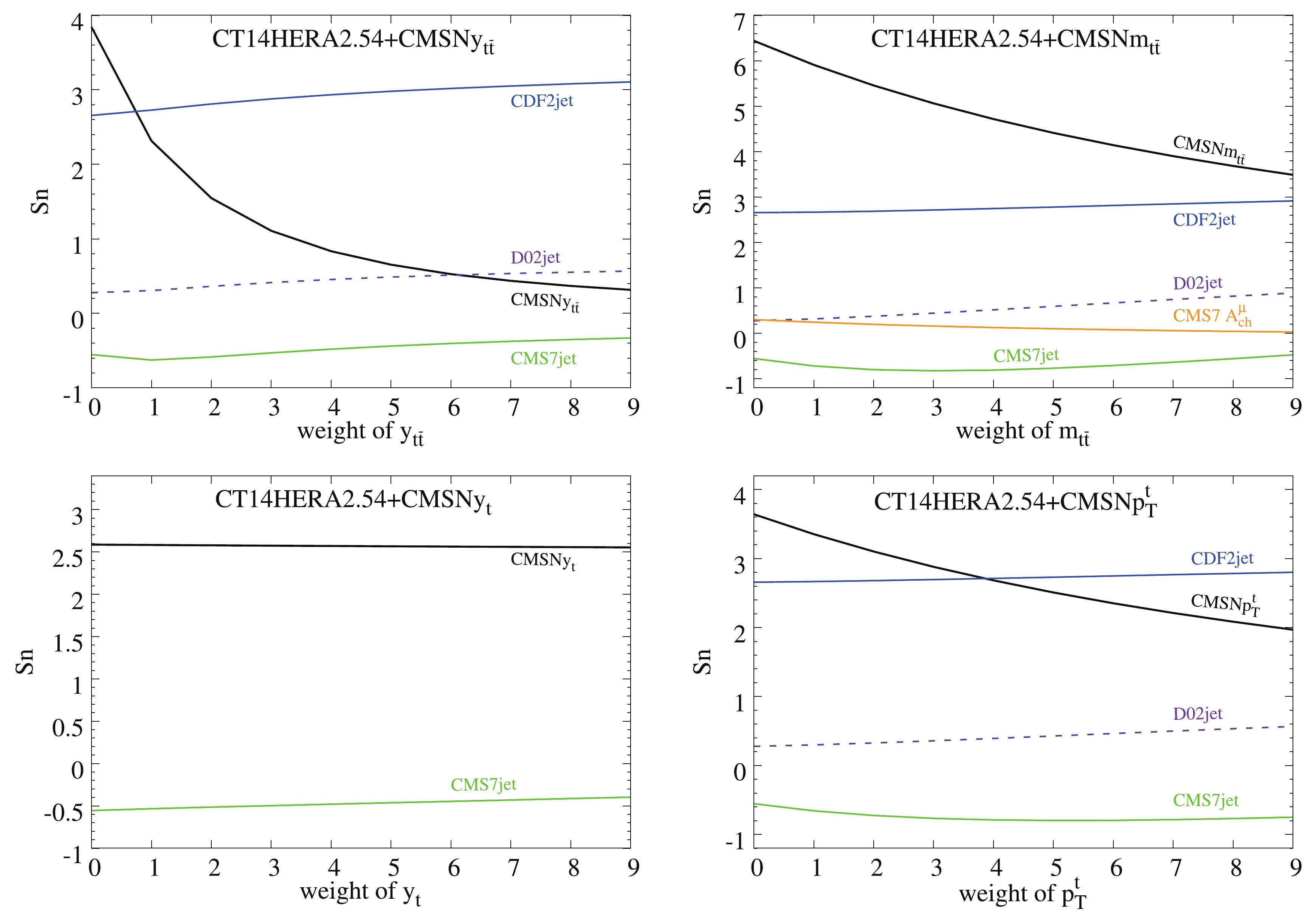
$ t \bar{t} $ data. This may be a result of strong tension from the data included in the CT14HERA2 PDF. To search for possible tensions between the single differential$ t \bar{t} $ data from ATLAS and CMS and the data sets included in the CT14HERA2 PDFs, we increase the weight of the$ t\bar t $ data when updating the CT14HERA2 PDFs using ePump. We consider weights from zero to nine for the single differential$ t\bar t $ data individually to test the tension among the$ t\bar t $ data and other data included in the CT14HERA2 PDF. The weight zero case is just the CT14HERA2 fit, without any change. The weight one case corresponds to the CT14HERA2 fit with$ t\bar t $ data included individually. Weight larger than one is equivalent to having more$ t\bar t $ data points with the same experimental uncertainties [18]. Instead of$ \chi^2 $ , we present the change in goodness-of-fit for each data point using the variable$ S_n $ [26], which can be treated as a rescale of$ \chi^2 $ based on the number of data points in the data. Values of$ S_n $ between$ -1 $ and$ 1 $ correspond to a good fit (at the 68% C.L.); large positive values of$ S_n $ ($ \gtrsim 2 $ ) correspond to a poor fit, while large negative values ($ \lesssim -2 $ ) indicate an unusually good fit. If we increase the weight of the ATLAS and CMS 8 TeV$ t \bar t $ data in the fit, the$ S_n $ of the$ t \bar t $ data decreases with reduced$ \chi^2 $ , as it should be; when the weight of the$ t \bar t $ data becomes large, the$ S_n $ of some data in CT14HERA2 may increase by a noticeable amount. If some of the data in CT14HERA2 have tension with the$ t \bar t $ data, the$ S_n $ of those data will become larger when the weight of the$ t \bar t $ data increases. We find that most of the data in CT14HERA2 do not show significant tension with the 8 TeV single differential ATLAS and CMS$ t\bar t $ data. However, some data in CT14HERA2 do show tension with the$ t\bar t $ data. In Figs. 8-9, we show the change in$ S_n $ for some data in CT14HERA2 as the weight of the$ t\bar t $ data increases from 0 to 9. We observe that some of the data in CT14HERA2 has a minor change in$ S_n $ as the weight of the$ t \bar t $ data increases. For example, we see that the$ S_n $ of the CDF jet data [9] and the D0 jet data [10] increases the most, while the$ S_n $ of the CMS 7 TeV jet data [12] decreases slightly when the weight of the ATLAS normalized$ |y_{t\bar t}| $ data or CMS normalized$ p^t_T $ data increases. As a result, we did not observe strong tension on the ATLAS and CMS single differential$ t \bar{t} $ data with respect to the data included in the CT14HERA2 PDF. However, we do observe that the jet data are relatively more sensitive to the inclusion of the$ t \bar{t} $ data. This is quite reasonable, as the jet data provide a constraint on the gluon PDF, as the$ t \bar{t} $ data do. The inclusion of the$ t \bar{t} $ data would form a "competitive" relationship with the jet data for constraining the gluon PDF.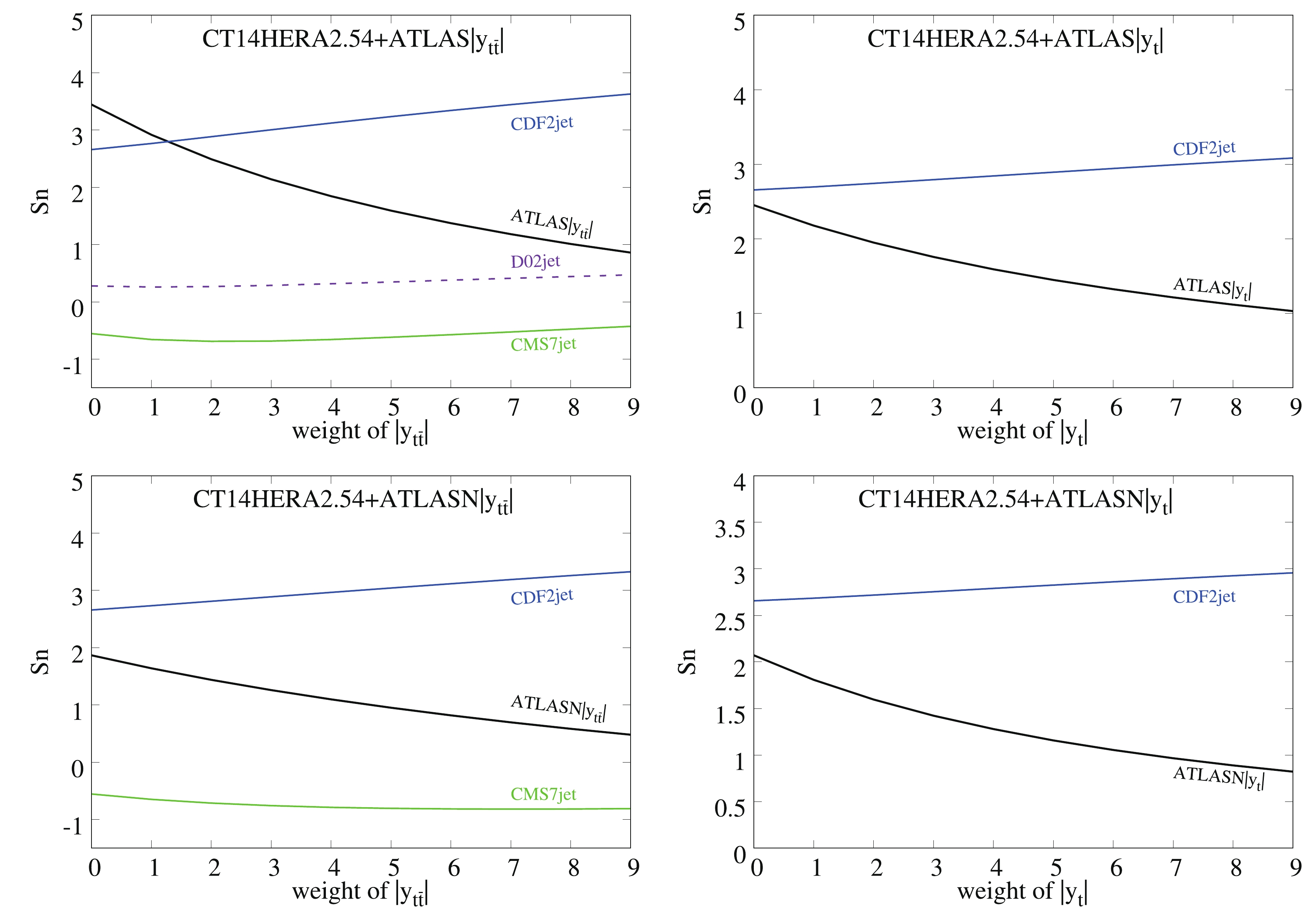
Figure 8. (color online) Equivalent Gaussian variable Spartyness
$ S_n $ of some data in ePump updated CT14HERA2.54 versus weight of the ATLAS absolute and normalized data for the absolute value of the rapidity$ |y_t| $ of the top quark distribution and top-quark pair rapidity$ |y_{t\bar t}| $ distribution at 8 TeV. -
As shown in the previous section, before the
$ t \bar{t} $ data, the gluon PDF of the CT14HERA2 receives a suitable constraint from the jet data, i.e., CDF [9], D0 [10], ATLAS [11], and CMS [12]. To see the impact of the$ t\bar t $ data on the gluon PDF, it is necessary to suppress the contribution from the jet data. For this purpose, first, we generated the Hessian eigenvector sets "CT14HERA2mJ" ("mJ" here means "minus jet") by global analysis after removing the four inclusive jet production data from Tevatron and LHC Run I in the CT14HERA2 fit. Then, we updated CT14HERA2mJ PDFs using ePump by including$ t\bar t $ data one by one. In this section, we provide comparisons of the CT14HERA2mJ before and after the ePump updating by adding the ATLAS and CMS 8 TeV$ t\bar t $ single differential cross section data as a function of$ y_{t\bar t} $ ,$ m_{t\bar t} $ ,$ y_t $ , and$ p^t_T $ . -
We first check the correlation between the absolute and normalized differential
$ t\bar t $ data and the CT14HER2mJ g($ x, Q = 100 $ GeV) PDF. Without inclusion of the jet data in the CT14HER2mJ, the gluon PDF receives constraints mostly from the deep inelastic scattering (DIS) data, demonstrating a behavior different from that of the gluon in the CT14HERA2 PDF. As shown in Fig. 10, the correlation between$ t\bar t $ data and the gluon CT14HER2mJ PDF keeps the main features as those of the gluon PDF in the CT14HERA2 PDF shown in Fig. 1.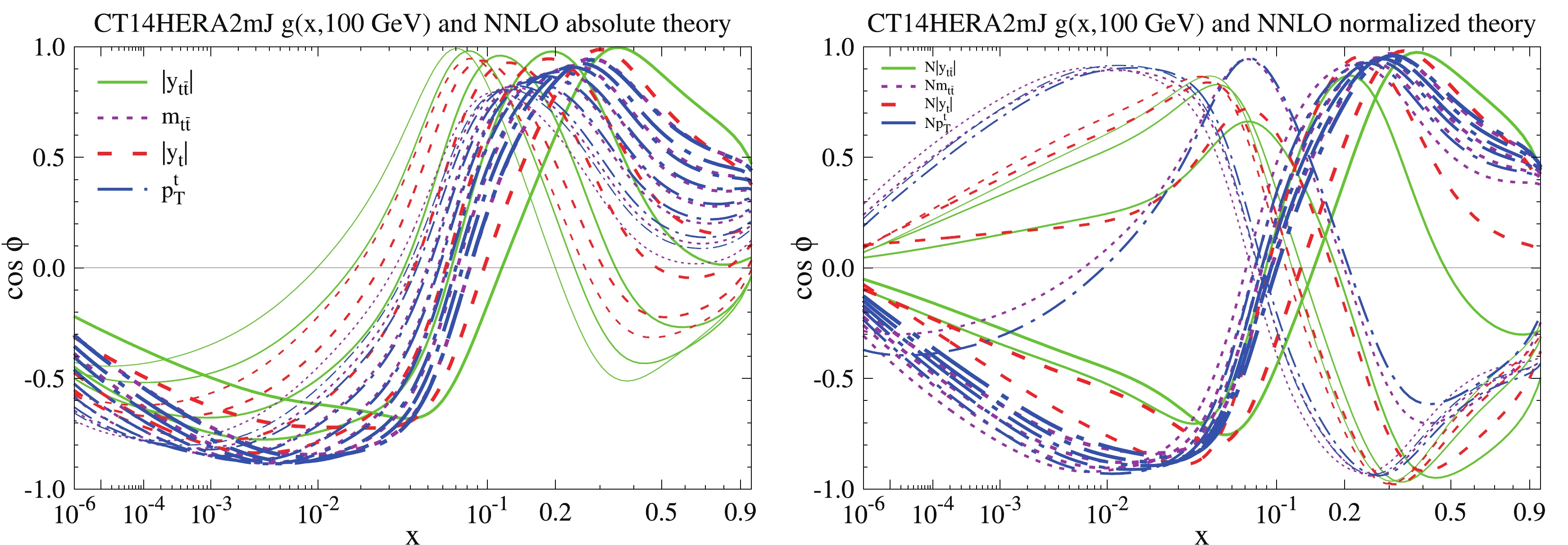
Figure 10. (color online) Correlation cosine
$ \cos \phi $ between CT14HERA2mJ$g(x,Q = 100\;{\rm GeV})$ PDF and fastNLO predictions for each bin of the absolute (left) and normalized (right)$ |y_{t\bar t}| $ (solid green),$ m_{t\bar t} $ (dark magenta),$ |y_t| $ (red), and$ p^t_{T} $ (blue) top-quark differential distributions. -
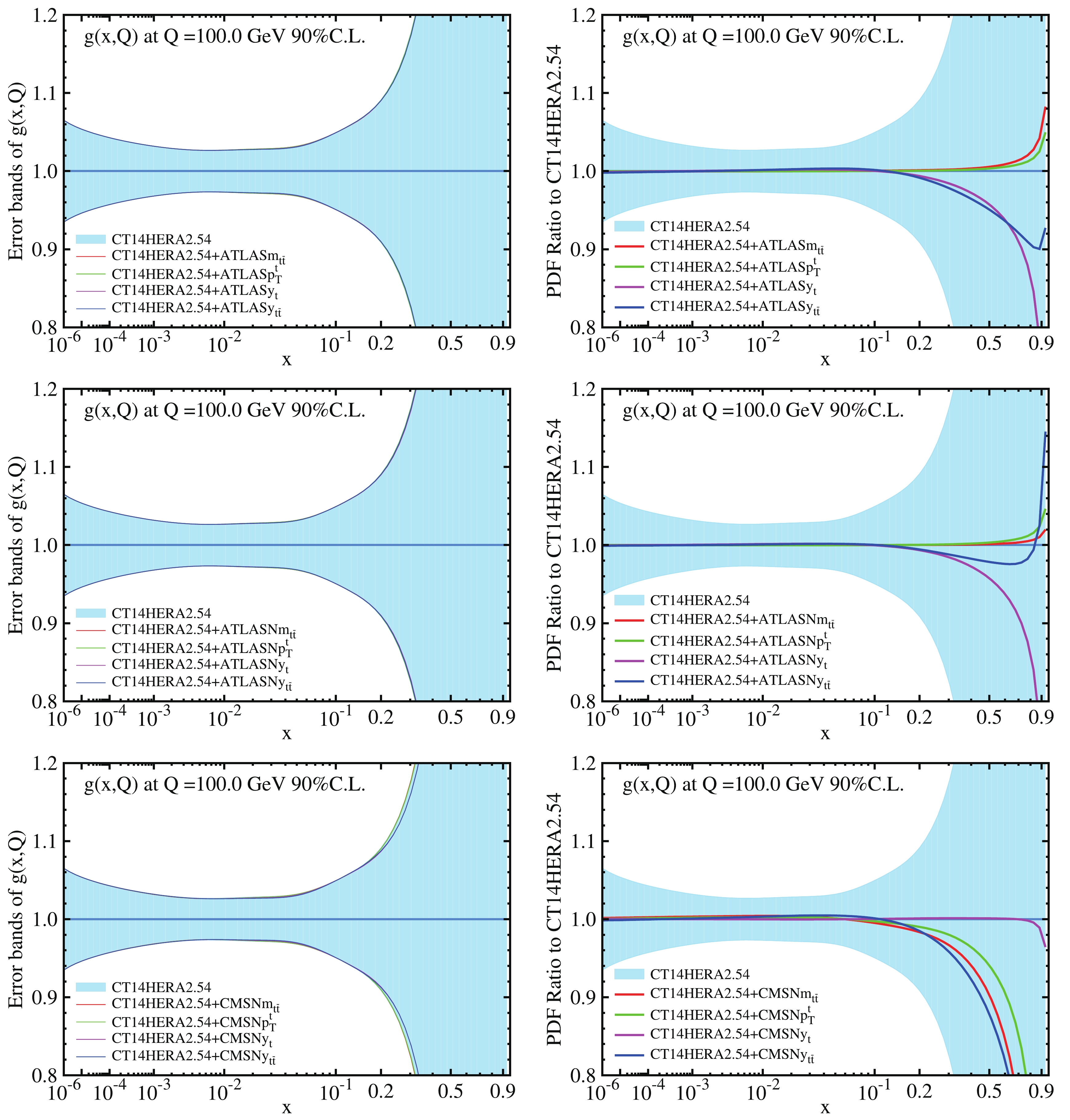
In Figs. 11 and 12, we show the ePump updated PDFs, starting from the CT14HERA2mJ PDFs and including the absolute and normalized ATLAS 8 TeV
$ t\bar t $ data one by one. The impact on the gluon PDF from those$ t\bar t $ data can be seen by comparing the difference between the gluon PDF before and after ePump updating. It is apparent that, without the jet data in the fit, the CT14HERA2mJ uncertainty band is larger than the CT14HERA2 band, the absolute${\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,${\rm d}\sigma/{\rm d}|y_t|$ and normalized$1/\sigma \;{\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}|y_t|$ data have a larger impact on the central PDF (and to a smaller extent on the uncertainty band) of the CT14HERA2mJ gluon PDF.
Figure 11. (color online) Gluon PDF ratios for ePump-updated CT14HERA2mJ+ATLAS
$ |y_{t\bar t}| $ , CT14HERA2mJ+ATLAS$ m_{t\bar t} $ , CT14HERA2mJ+ATLAS$ |y_t| $ , and CT14HERA2mJ+ATLAS$ p^t_T $ PDFs, which are obtained by including ATLAS 8 TeV absolute${\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,${\rm d}\sigma/{\rm d}m_{t\bar t}$ ,${\rm d}\sigma/{\rm d}|y_t|$ , and${\rm d}\sigma/{\rm d}p^t_T$ data, over the best-fit of the base CT14HERA2.54 gluon PDFs.
Figure 12. (color online) Gluon PDF ratios for ePump-updated CT14HERA2mJ+ATLAS
$ |y_{t\bar t}| $ , CT14HERA2mJ+ATLAS$ m_{t\bar t} $ , CT14HERA2mJ+ATLAS$ |y_t| $ , and CT14HERA2mJ+ATLAS$ p^t_T $ PDFs, which are obtained by including ATLAS 8 TeV normalized$1/\sigma \; {\rm d}\sigma/{\rm d}|y_{t\bar t}|$ ,$1/\sigma \; {\rm d}\sigma/{\rm d} m_{t\bar t}$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}|y_t|$ , and$1/\sigma \; {\rm d}\sigma/{\rm d}p^t_T$ data, over the best-fit of the base CT14HERA2.54 gluon PDFs.More specifically, we observe an increase in the CT14HERA2mJ best fit gluon PDF for
$ 10^{-4} \lesssim x \lesssim 0.15 $ and a decrease for$ x \gtrsim 0.15 $ after including${\rm d}\sigma/{\rm d}|y_{t\bar t}|$ and${\rm d}\sigma/{\rm d}|y_t|$ data. We also observe a small reduction in the gluon PDF uncertainty bands for$ x \sim 0.05 $ . However, there is still no obvious impact on the CT14HERA2mJ gluon PDF after including the absolute${\rm d}\sigma/{\rm d}m_{t\bar t}$ ,${\rm d}\sigma/{\rm d}p^t_T$ and normalized$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}p^t_T$ data. The results shown in Figs. 11 and 12 directly confirm our understanding from the last section that the reason we see only minor impacts on the CT14HERA2 gluon PDF is because the CT14HERA2 gluon PDF is well constrained by the four jet data sets included in the CT14HERA2 PDF. The removal of the jet data increases the constraining power of the$ t \bar t $ data, but the impact is still smaller than that of the jet data sets. -
In this section, by including the normalized CMS 8 TeV
$1/\sigma \;{\rm d}\sigma/{\rm d}y_{t\bar t}$ ,$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ ,$1/\sigma \;{\rm d}\sigma/ {\rm d}y_t$ , and$1/\sigma \; {\rm d}\sigma/ {\rm d}p^t_T$ data one by one, we update the CT14HERA2mJ PDFs. The impact on gluon PDF from$ t\bar{t} $ data can be seen by comparing the difference between the gluon PDF before and after the ePump updating. From Fig. 13, we see that, without the jet data in the fit, the normalized differential CMS 8 TeV$ t\bar t $ data$ y_{t\bar t} $ ,$ m_{t\bar t} $ ,$ y_t $ , and$ p^t_{T} $ have a rather obvious impact on both the central predictions and uncertainty bands of the CT14HERA2mJ gluon PDF in the region$ 10^{-4} \lesssim x \lesssim 0.6 $ , i.e., each$ t\bar t $ data point increases the gluon PDF in the region$ 10^{-4} \lesssim x \lesssim 0.15 $ , while each$ t\bar t $ data point decreases it in the region$ x \gtrsim 0.15 $ ; however, the updated gluon PDFs in the four cases are well within the uncertainty bands of PDFs. -
In Fig. 14, we compare gluon PDFs from CT14HERA2mJ, CT14HERA2mJpJ, and CT14HERA2mJ+CMS7J. Here, CT14HERA2mJpJ and CT14HERA2mJ+CMS7J are obtained by ePump by adding four jet data [9-12] into the CT14HERA2mJ fit and including the CMS 7 TeV inclusive jet data [12] into the CT14HERA2mJ fit. We first observe that the CT14HERA2mJpJ gluon PDF has a smaller uncertainty band than the CT14HERA2mJ+CMS7J gluon PDF, which demonstrates that the four jet data have a strong impact on the gluon PDF. It is therefore understandable why there is no significant impact on the CT14HERA2 PDF from the
$ t\bar t $ data. Despite the difference in uncertainty between the CT14HERA2mJpJ gluon PDF and CT14HERA2mJ +$ t\bar t $ (from ATLAS and CMS) gluon PDF, it is worth noting that both the$ t\bar t $ (from ATLAS and CMS) and jet data have a similar impact on the gluon central PDF, which shows the agreement between the impact on the gluon PDF from$ t\bar t $ and jet data.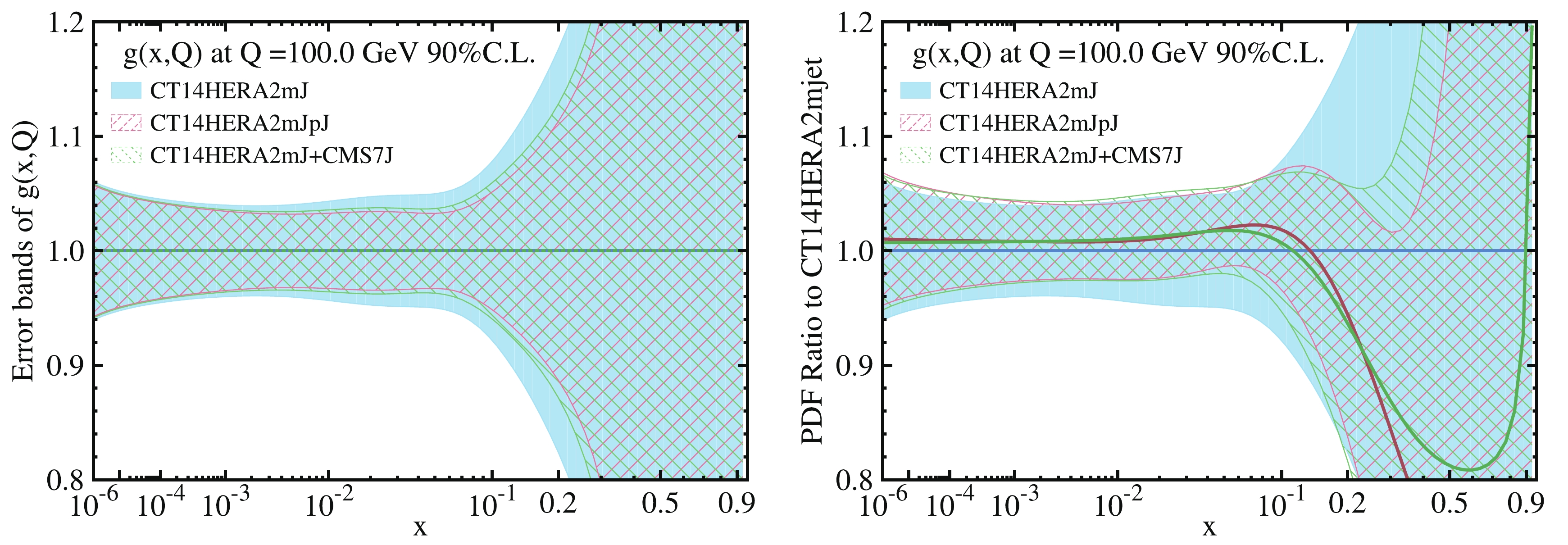
Figure 14. (color online) Left plot shows comparison of the gluon PDF error band from CT14HERA2mJ (blue band), CT14HERA2mJpJ (red shaded band), and CT14HERA2mJ+CMS7J (green shaded band); note that each error band is normalized to its own gluon central PDF. Right plot shows the gluon PDF ratios for CT14HERA2mJ (blue), CT14HERA2mJpJ (red), and CT14HERA2mJ+CMS7J (green) over the best-fit of the base CT14HERA2mJ (blue band).
It is clear that the CMS 7 TeV inclusive jet data dominate the contribution to constraining the gluon PDF among the four jet data. Therefore, in the following study, we consider only the CMS 7 TeV inclusive jet data.
It is worth noting that the
$ t\bar t $ production data have a smaller number of data points compared with the jet data, by approximately a factor of 10. After testing the impact on CT14HERA2 and CT14HERA2mJ PDFs, it is interesting to compare the sensitivity per data point for the jet and$ t\bar{t} $ data. To see this, a hypothetical weight is implemented in the single differential$ t\bar{t} $ production data with the weight set to be equal to the ratio between the number of data points of the CMS 7 TeV jet data and the$ t\bar{t} $ data. Taking the CMS 8 TeV normalized$ p^t_T $ distribution as an example, the hypothetical weight applied to the data is equal to$ w = 133/8 = 16.6 $ . In practice, a larger weight can arise by increasing the event statistics or reducing the experimental error.In this naive estimation, we assume the central values of the measurement do not change, such that the central prediction after updating with the hypothetical weight is rather less meaningful. For this reason, in what follows, we show a comparison of the PDFs' uncertainty. In Fig. 15, we compare the impact of the CMS 7 TeV inclusive jet data and CMS 8 TeV normalized
$ t\bar{t} $ production data with the hypothetical weight on the gluon PDF uncertainty. We find that the weighted$ t\bar{t} $ production data provide a stronger constraint on the gluon PDFs for$ 10^{-3} \lesssim x \lesssim 5 \times 10^{-2} $ . It is also true for the absolute ATLAS 8 TeV$ t\bar{t} $ production data. With the hypothetical weight equal to the ratio of number of jets and$ t\bar t $ data points, the absolute$ t\bar{t} $ production data provide approximately the same constraint on the gluon PDF as the jet data.
Figure 15. (color online) Comparison of the gluon PDF error band from CT14HERA2mJ+CMS7J (red shaded band), CT14HERA2mJ+CMSN
$ y_{t\bar t} $ W13.3 (top left, green shaded band), CT14HERA2mJ+CMS8N$ m_{t\bar t} $ W19.0 (top right, green shaded band), CT14HERA2mJ+CMS8N$ p_t $ W16.6 (bottom left, green shaded ban), and CT14HERA2mJ+CMS8N$ y_t $ W13.3 (bottom right, green shaded ban) PDFs, obtained by adding CMS 7 TeV inclusive jet data, CMS 8 TeV normalized$1/\sigma \; {\rm d}\sigma/{\rm d}y_{t\bar t}$ data with weight 13.3,$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ data with weight 19.0,$1/\sigma \; {\rm d}\sigma/{\rm d}y_t$ data with weight 13.3, and$1/\sigma \; {\rm d}\sigma/{\rm d}p^t_T$ data with weight 16.6 at Q = 100 GeV and at 90% C.L., with the base CT14HERA2mJ gluon PDF (blue band).Next, we examine the impact of the CMS 8 TeV normalized
$1/\sigma \; {\rm d}\sigma/{\rm d}y_{t\bar t}$ data and CMS 7 TeV inclusive jet via ePump on the observables. The Higgs production rate through gluon-gluon fusion at the LHC is sensitive to the gluon PDF in the middle-x region, which is constrained by both CMS 7 TeV inclusive jet and$1/\sigma \; {\rm d}\sigma/{\rm d}y_{t\bar t}$ data. In Fig. 16, we show the correlation ellipses between CMS 8 TeV normalized${\rm d}\sigma/{\rm d}y_{t\bar t}$ data for various rapidity bins and Higgs production through gluon-gluon fusion at 13 TeV for CT14HERA2mJ+CMSN$ y_{t\bar t} $ (black), CT14HERA2mJ+CMSN$ y_{t\bar t} $ W13.3 (dark blue), and CT14HERA2mJ+CMS7J (red). The central prediction of the CT14HERA2mJ+CMSN$ y_{t\bar t} $ W13.3 is obtained by assuming the central measurement is the same as that in CT14HERA2mJ+CMSN$ y_{t\bar t} $ .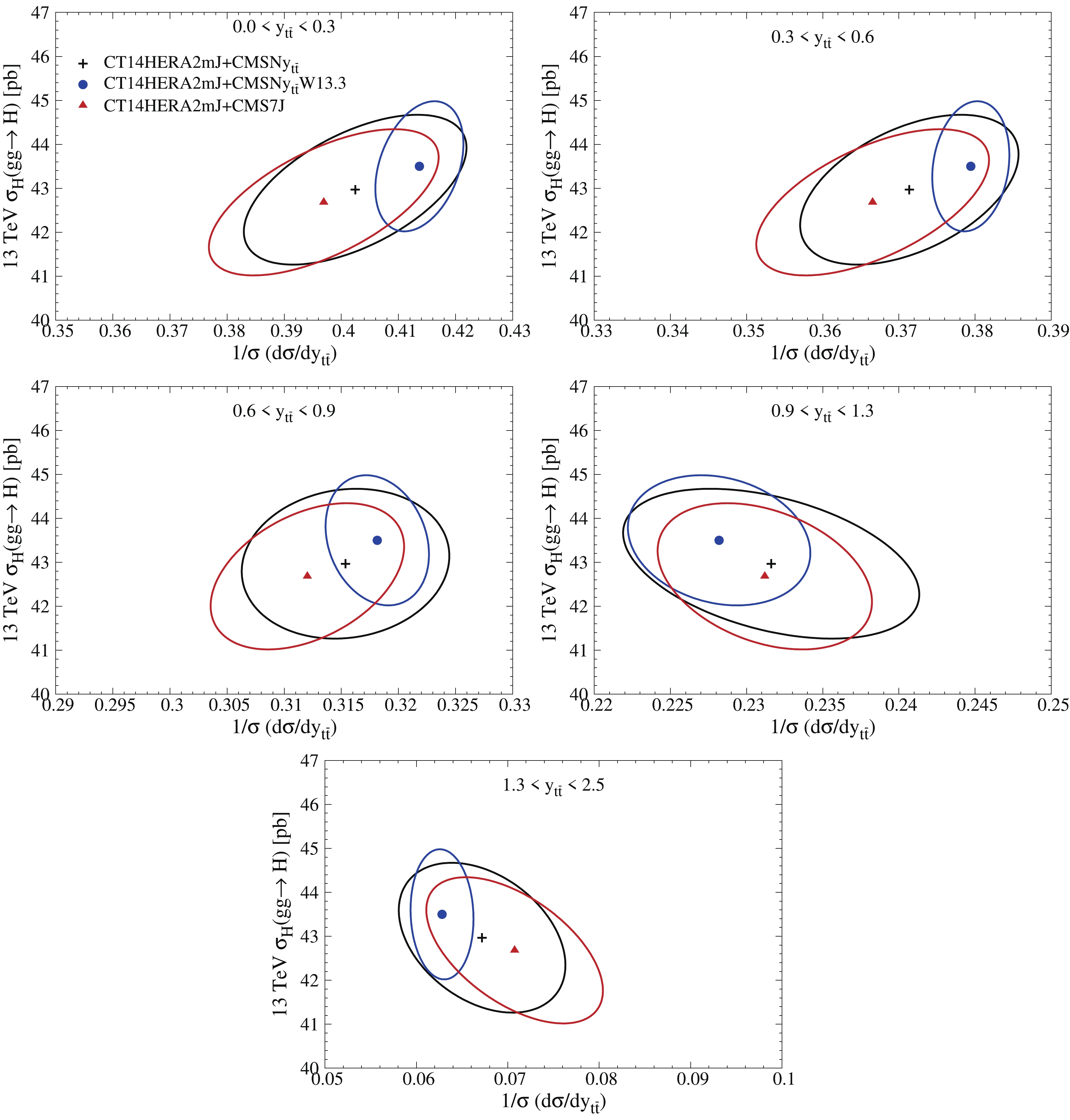
Figure 16. (color online) Correlation ellipses between the Higgs production rate via gluon-gluon fusion and the normalized
$1/\sigma \; {\rm d}\sigma/\sigma y_{t\bar t}$ differential cross section at 13 TeV for ePump updated CT14HERA2mJ+CMSN$ y_{t\bar t} $ , CT14HERA2mJ+CMSN$ y_{t\bar t} $ W13.3, CT14HERA2mJ+CMS7J, and CT14HERA2mJ PDFs; PDF uncertainty is at 90% C.L. -
The top-quark mass sensitivity of the differential top pair production distributions as a function of
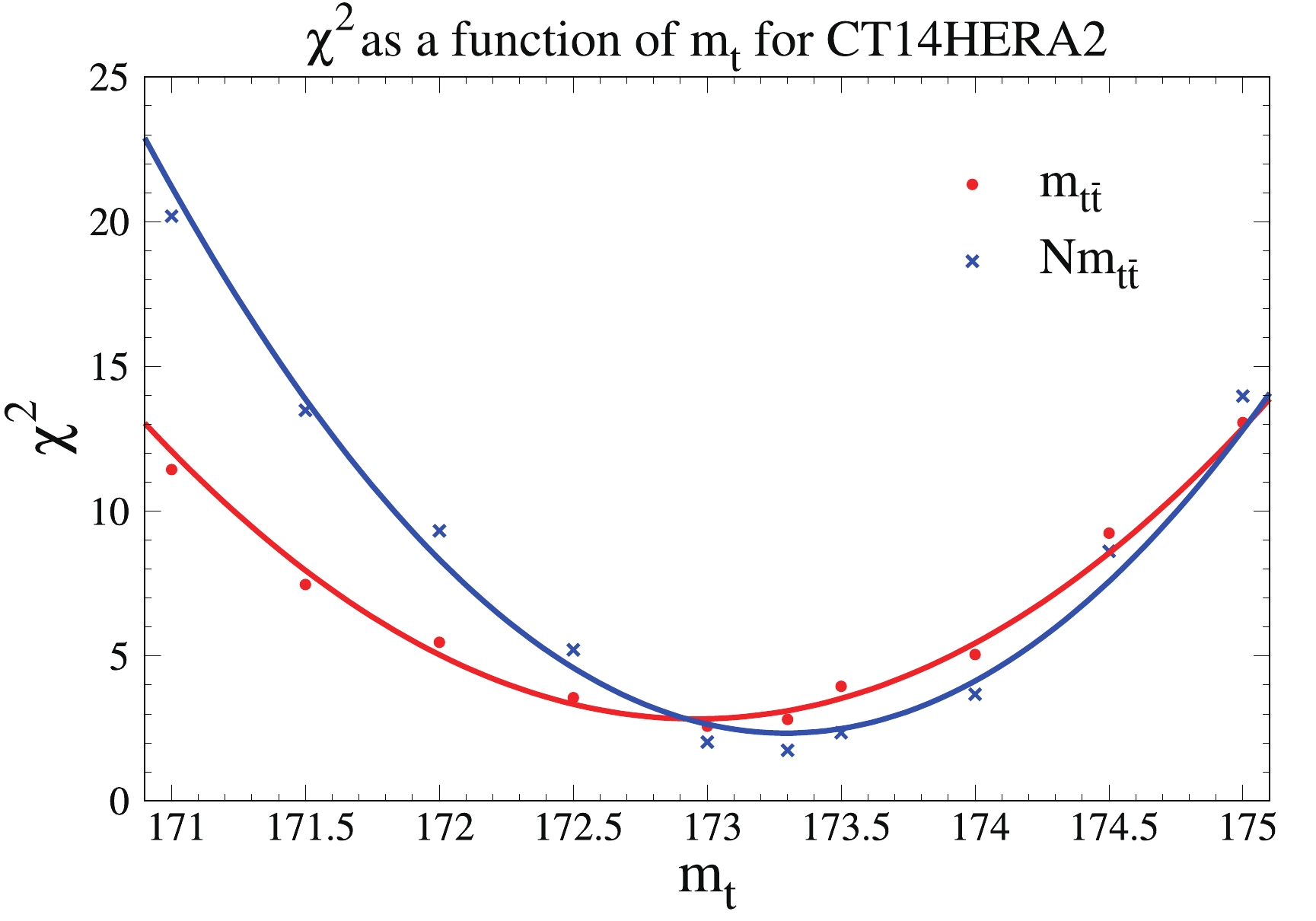
$ m_{t\bar t} $ has been studied in Refs. [27, 28], where the authors found that the top quark mass dependence is pronounced in the$ m_{t\bar t} $ distribution. Ref. [13] also reported the sensitivity with variations in$ m_t $ of the differential distributions as a function of$ m_{t\bar t} $ ,$ y_{t\bar t} $ ,$ y_t $ , and$ p^t_T $ ; it was found that the invariant mass distribution of the top pair and the top transverse momentum$ p_T^t $ distributions have stronger dependence on the top mass than the top rapidity ($ y_t $ ) and the rapidity ($ y_{t\bar t} $ ) of the top pair. By studying the top-quark mass dependence of the differential top pair production distributions as a function of$ m_{t\bar t} $ , another way to determine the mass of the top quark could be provided. In Fig. 17, we show the chi-square function,$ \chi^2 $ versus the top-quark mass for the absolute and normalized 8 TeV single differential cross sections as a function of the invariant mass$ m_{t\bar t} $ of the top-quark pair using the Monte-Carlo numerical calculation program MadGraph [29] with CT14HERA2 PDFs and the same set-up as in Refs. [4, 5]. The${\rm d}\sigma/{\rm d}m_{t\bar t}$ is shown in red; the$1/\sigma \; {\rm d}\sigma/{\rm d}m_{t\bar t}$ is shown in green. The parabolic curves are fitted from calculation with many values of top mass from$ 171.0 $ GeV to$ 175.0 $ GeV. The two curves have slightly different minima, i.e.,$ m_t = 173.0 $ GeV for absolute distributions and$ m_t = 173.5 $ GeV for normalized distributions. This may occur because of the anti correlation of the the inverse of the total cross section. We performed the same study for the$ p^t_T $ ,$ |y_t| $ , and$ |y_{t\bar t}| $ distributions, and we found that the differential cross sections as a function of$ p^t_T $ ,$ |y_t| $ , and$ |y_{t\bar t}| $ do not depend on the top-quark mass. -
In this paper, we examined the impact of the
$ t\bar t $ data (top quark pair invariant mass$ m_{t\bar t} $ , top quark pair rapidity$ y_{t\bar t} $ , individual top quark/antiquark transverse momentum$ p^t_T $ , and absolute value of the top quark rapidity$ |y_t| $ ) on the CT14HERA2 and CT14HERA2mJ PDFs using the ePump package. From Fig. 2, we observe that, when adding the$ t \bar t $ data one by one to a global data set, CMS normalized distributions show larger constraining power than the ATLAS absolute and normalized data. Furthermore, we observed different impacts from various distributions on the gluon PDF. The reasons are as follows. First, the normalized data yield stronger constraints than the absolute data, as expected, because the dominant collider luminosity error present in the absolute data cancels in the normalized data. Because of their much smaller error, the normalized data generally provide a much stronger constraint on PDFs. Second, different differential cross section data could have different degrees of sensitivity to gluon PDFs. For example, it is expected that the rapidity distributions, either the rapidity of t or the$ t \bar t $ pair, are more sensitive to gluon PDFs than other distributions. Moreover, to extract PDFs from the data, it is also important to use state-of-art theoretical calculations in the global analysis. It has been shown that both the transverse moment of t or the$ t \bar t $ pair, as well as the invariant mass of the$ t \bar t $ pair, could suffer large higher order QCD and electroweak corrections. However, in the current analysis, we only include up to NNLO QCD corrections. In Fig. 17, we show the top mass dependence of the differential top pair production distributions at 8 TeV. We found that only the${\rm d}\sigma/{\rm d}m_{t\bar t}$ distribution is sensitive to the top-quark mass, with the minimum at approximately$ 173.3 $ GeV. Because the invariant mass of the$ t \bar t $ pair is expected to be sensitive to the value of the top quark mass$ m_t $ , the theoretical predictions of both low and high mass bins are sensitive to higher order QCD and electroweak corrections. Hence, the impact of the normalized and absolute data could be different, depending on the accuracy of the integrated cross section value used in the normalized data measurement. Note that all the top-quark pair production data have a minor impact on the CT14HERA2 gluon PDF when jet data are included in the global analysis. This occurs because the number of data points for the$ t\bar t $ data is much less than that for the jet data. By giving a hypothetical weight to the$ t\bar t $ data that reflects the ratio of the number of data points between the jet data and$ t\bar t $ data, the$ t\bar t $ data show good agreement with the impact from jet data, with similar strength. Hence, the sensitivity per data point of$ t\bar t $ data is similar to that of jet data, while the total sensitivity of the data set depends on the total number of data points. -
We would like to thank Joey Huston and C. -P. Yuan for many helpful discussions. We are very grateful to Joey Huston for proofreading.
The impact of ATLAS and CMS single differential top-quark pair measurements at ${\sqrt{ s}\bf{=8}}$ TeV on CTEQ-TEA PDFs
- Received Date: 2020-08-15
- Accepted Date: 2020-11-02
- Available Online: 2021-02-15
Abstract: By applying the Error PDF Updating Method, we analyze the impact of the absolute and normalized single differential cross-sections for top-quark pair production data from the ATLAS and CMS experiments at the Large Hadron Collider, at a center-of-mass energy of







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: