-
According to the theory of the strong interaction, quantum chromodynamics (QCD) [1], gluons are able to interact with one another, which suggests the existence of a particle consisting solely of gluons, the glueball. The search for the glueball has a long history, however evidence of its existence is still vague. Being short of reliable glueball production and decay mechanisms makes the corresponding investigation rather difficult. Another hurdle hindering the search for the glueball lies in the fact that they usually mix heavily with the quark states, somehow with the exception of exotic glueballs [2].
Scalar glueballs which have the quantum numbers
JPC=0++ are suggested to be the lightest glueballs by lattice calculation, displaying a mass of around1600−1700 MeV with an uncertainty of about100 MeV [3-6]. Experimentally, there exist three isosinglet scalars that exist in this mass range:f0(1370) ,f0(1500) , andf0(1710) . The absence of theγγ→KˉK orπ+π− pair production modes throughf0(1500) excludes the possibility of a largenˉn content withinf0(1500) [7, 8]. On the other hand, thef0(1500) has a smallKˉK decay branching rate [9-12], implying that its main content is unlikely to besˉs . Various peculiar natures suggest thatf0(1500) might be a scalar glueball or a glue rich object [13]. In a large mixing model, as discussed in Refs. [13-16], glue is shared betweenf0(1370) ,f0(1500) , andf0(1710) . The isosinglet scalarf0(1370) is mainly constructed ofnˉn ,f0(1500) is thought to be glue predominant, andf0(1710) has a highsˉs content.Evidence for pseudoscalar
0−+ glueballs is still weak [17].E(1420) andι(1440) observed by Mark II were early candidates of pseudoscalar glueballs [18-21]. However,E(1420) was later considered to be1+ meson and renamedf1(1420) , whileι(1440) is still thought to be a pseudoscalar, now known asη(1405) [22]. The modeη(1405)→ηππ was observed at BES II inJ/ψ decay [23] and was confirmed inˉpp annihilation [24]. It should be noted thatη(1405) was observed in neitherηππ norKˉKπ channels inγγ collisions by L3 [25]; this implies thatη(1405) has a large glue component since glueball production is suppressed inγγ collisions. It is also worth mentioning that the quenched lattice and QCD sum rule calculation predict that the0−+ glueball mass might be above2 GeV [4, 26, 27], though Gabadadze argued that the pseudoscalar glueball mass in full QCD could be much less than the quenched lattice result in Yang-Mills theory [28]. Furthermore, despiteη(1405) fitting well with the fluxtube model [29] and roughly fitting with theη -η′ -G mixing calculations [30], a recent triangle singularity mechanism analysis reveals thatη(1405) andη(1475) might be the same state [31]. For further properties of pseudoscalar glueballs, readers may refer to recent studies [32, 33].In this paper, motivated by studying the glueball production and decay mechanisms, we discuss glueball production in
ηc decay by introducing a model for the gluon-pair-vacuum interaction vertices; namely the0++ model, as shown in Fig. 1. We assume the gluon pair is created homogeneously in space with equal probability. Comparing to the3P0 model [34-43], which models quark-antiquark pair creation in a vacuum, we formulate an explicit vacuum gluon-pair transition matrix and estimate the strength of the gluon-pair creation. Employing the0++ model, we then investigate theηc andηb decays to scalar and pseudoscalar glueballs. Based on previous glueball studies, we takef0(1710) andf0(1500) as scalar glueball candidates, andη(1405) as a pseudoscalar glueball candidate. The corresponding decay widths and branching fractions are calculated.The rest of the paper is arranged as follows. After the introduction, we construct a model for gluon-pair-vacuum interaction vertices in Sec. 2. The partial widths of
ηc→f0(1500)η(1405) ,ηb→f0(1500)η(1405) andηb→f0(1710)η(1405) are evaluated in Sec. 3. Last section is remained for summary and outlooks. -
In quantum field theory, the physical vacuum is thought of as the ground state of energy, with constant particle field fluctuations. Therefore, there are certain probabilities for quark pairs and gluon pairs with vacuum quantum numbers to appear in the vacuum. It is reasonable to hypothesize that gluon pairs would be created with equal amplitude in space, akin to the quark-antiquark pairs in the
3P0 model. As they are created from the vacuum, the gluon pairs possess the quantum numbersJPC=0++ .We may argue the soundness of the
0++ scheme like this: in the language of Feynman diagram, the dominant contribution to the vacuum-gluon-pair coupling may stem from the processes where two additional gluons are produced from either a parent meson or the first two gluons. It should be noted that although by naive order counting of the strong coupling, one may presumably say these processes are dominant, in fact the nonperturbative effect may impair this analysis. The most straightforward way to configure the vacuum-gluon-pair coupling is to attribute various contributions to an effective constant, analogous to the3P0 model. This is somewhat similar to the case of hadron production, where only limited hadron production processes have been proved to be factorizable, while all other processes are usually evaluated via assumptions or models.In the remainder of our study, we investigate glueball pair production in pseudoscalar quarkonium decay using the
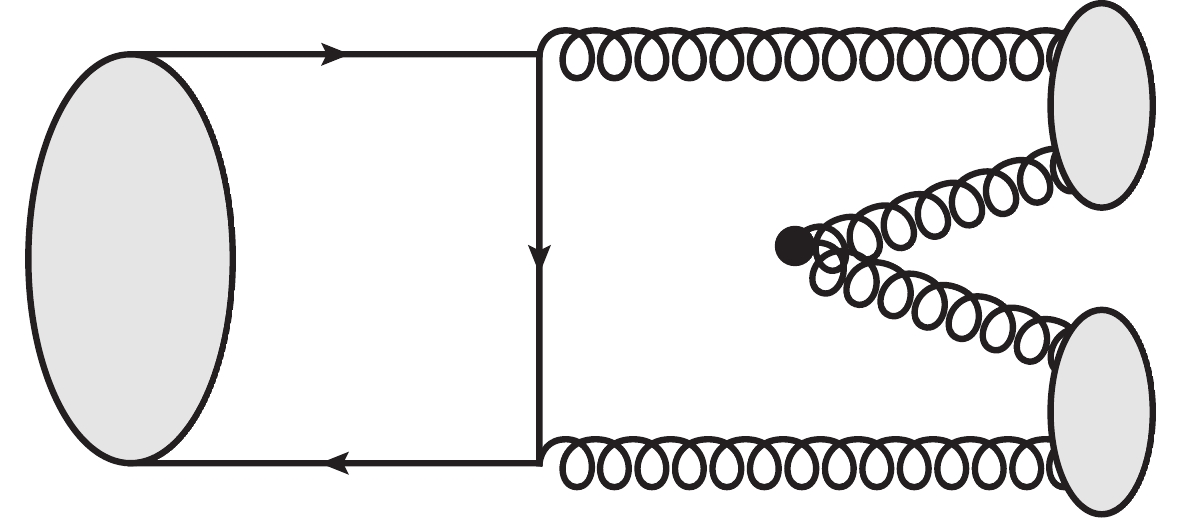
0++ model. The transition amplitude ofηc exclusive decay to double glueballs for instance, as shown in Fig. 1, can be formulated as⟨G1G2|T|ηc⟩=γg⟨G1G2|T2⊗(GcρσGcρσ)|ηc⟩ .

(1) Here,
G1 andG2 represent glueballs, whileγg denotes the strength of gluon pair creation in the vacuum, which in principle can be extracted by fitting to the experimental data. TheGcρσGcρσ term creates the gluon pair in the vacuum.T2 is the transition operator forηc annihilating to two gluons. The state|ηc⟩ andT2 can be expressed as|ηc⟩=√2Eηc∫d3kcd3kˉcδ3(Kηc−kc−kˉc)×∑MLηc,MSηc⟨LηcMLηcSηcMSηc|JηcMJηc⟩×ψnηcLηcMLηc(kc,kˉc)χcˉcSηcMSηc|cˉc⟩,

(2) T2=g2sˉcitaijγμcjAμaˉcmtbmnγνcnAνb .

(3) Here,
kc andkˉc represent the3 -momenta of quarks c andˉc ;ψnηcLηcMLηc(kc,kˉc) is the spatial wavefunction with n, L, S, and J the principal quantum number, orbital angular momentum, total spin and the total angular momentum of|ηc⟩ , respectively;χcˉc is the corresponding spin state;⟨LGMLGSGMSG|JGMJG⟩ is the Clebsch-Gordan (C-G) coefficient;gs denotes the strong coupling constant;ci ,Aμa andta respectively represent the quark fields, gluon fields and Gell-Mann matrices.Inserting the completeness relation
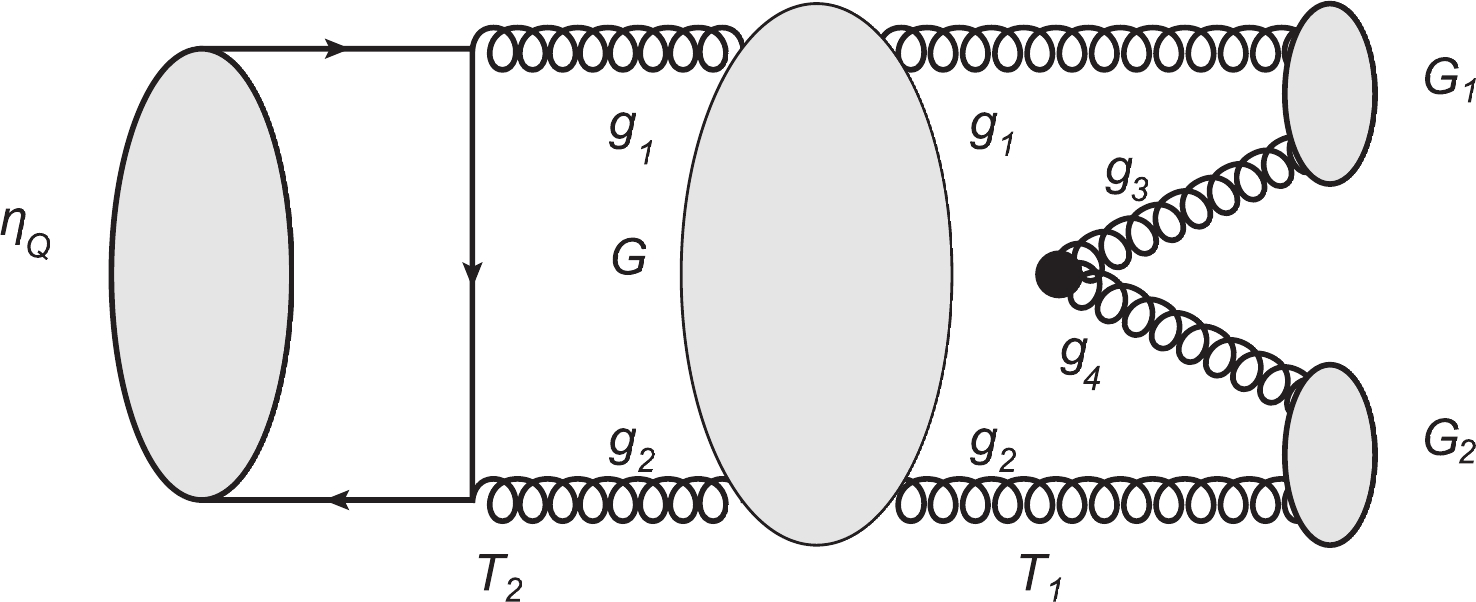
∑G|G⟩⟨G|=2EG into Eq. (1), we get⟨G1G2|T|ηc⟩=12EG∑Gγg⟨G1G2|GcρσGcρσ|G⟩⟨G|T2|ηc⟩≡12EG∑Gγg⟨G1G2|T1|G⟩⟨G|T2|ηc⟩+highorderterms ,

(4) where
|G⟩ is the shorthand notation for gluonsg1 andg2 emitted fromηc and the phase space integration is implied, as given in Eq. (8).T1 represents the operator responsible for theG→G1G2 transition.Noticing that the evaluation of the gluon-pair-vacuum interaction from first principles (QCD) is currently beyond our capability, we assume the interaction vertex shown in Fig. 2 can be modeled phenomenologically, in such a way that the transition matrix
T1 decomposes to:T1=I1⊗I2⊗Tvac ,

(5) where
Tvac signifies the vacuum-gluon pair transition operator, andIi are identity matrices indicating the quasi-free propagations ofg1 andg2 . The gluonsg3 andg4 are created in the vacuum, with their spin states|ms3,ms4⟩ having two different combinations. Please note that the gluons in the transition matrixT1 turn out to be massive, after experiencing nonperturbative evolutions.The total spin state of the gluon pair produced in the vacuum,
|S,MS⟩ , possessing the vacuum quantum number, being a singlet, can be formulated asχ340,0=1√2(|1,−1⟩ms3ms4+|−1,1⟩ms3ms4) .

(6) Subsequently,
Tvac can then be expressed asTvac=γg∫d3k3d3k4δ3(k3+k4)Y00(k3−k42)×χ340,0δcda†3c(k3)a†4d(k4) .

(7) Here,
k3 andk4 represent the3 -momenta of the gluonsg3 andg4 respectively,a†3c anda†4d are creation operators of gluons with color indices, andYℓm(k)≡|k|ℓYℓm(θk,ϕk) is theℓ th solid harmonic polynomial that gives out the momentum-space distribution of the produced gluon pairs.The state
|G⟩ should possess the quantum numbers of|ηc⟩ , i.e.JPCG=0−+ . As discussed in previous studies [44-47], the state might mix withηc , and thus can be parameterized as|G⟩=√2EG∫d3k1d3k2δ3(KG−k1−k2)×∑MLG,MSG⟨LGMLGSGMSG|JGMJG⟩×ψnGLGMLG(k1,k2)χ12SGMSGδab|ga1gb2⟩ ,

(8) where
k1 andk2 represent the3 -momenta of the gluonsg1 andg2 ,ψnGLGMLG(k1,k2) is the spatial wavefunction with n, L, S, J the principal quantum number, orbital angular momentum, total spin and the total angular momentum of|G⟩ , respectively.χ12 is the corresponding spin state, later on expressed as|SGMSG⟩ for the sake of calculation transparency.⟨LGMLGSGMSG|JGMJG⟩ is the C-G coefficient and reads⟨1m;1−m|00⟩ for the state|G⟩ . The associated normalization conditions are⟨G(KG)|G(K′G)⟩=2EGδ3(KG−K′G) ,

(9) ⟨gai(ki)|gbj(kj)⟩=δijδabδ3(ki−kj) ,

(10) ∫d3k1d3k2δ3(KG−k1−k2)ψG(k1,k2)ψG′(k1,k2)=δG′G,

(11) with
KG andK′G the corresponding3 -momenta. We have similar expressions for theG1 andG2 states.Equipped with the gluon-to-glueball transition operator
T1 and expressions for the initial and final states, we are now capable of evaluating the transition matrix element:⟨G1G2|T1|G⟩=γg√8EGEG1EG2∑(MLG,MSG),(MLG1,MSG1),(MLG2,MSG2)×⟨LGMLGSGMSG|JGMJG⟩⟨LG1MLG1SG1MSG1|JG1MJG1⟩×⟨LG2MLG2SG2MSG2|JG2MJG2⟩⟨χ13SG1MSG1χ24SG2MSG2|χ12SGMSGχ3400⟩IMLG,MLG1,MLG2(K)(δabδcdδacδbd)color-octet.

(12) Here, the momentum space integral
IMLG,MLG1,MLG2(K) can be written asIMLG,MLG1,MLG2(K)=∫d3k1d3k2d3k3d3k4δ3(k1+k2−KG)δ3(k3+k4)δ3(KG1−k1−k3)×δ3(KG2−k2−k4)ψ∗nG1LG1MLG1(k1,k3)ψ∗nG2LG2MLG2(k2 ,k4)×ψnGLGMLG(k1,k2)Y00(k3−k42) .

(13) For simplicity, it is reasonable to assume that the glueball and
|G⟩ state wavefunctions to be in a harmonic oscillator (HO) form;ψnLM(k)=NnLexp(−R2k22)YLM(k)P(k2) ,

(14) where
k is the relative momentum between two gluons inside the states,NnL is the normalization coefficient andP(k2) is a polynomial ofk2 [38].⟨χ13SG1MSG1χ24SG2MSG2|χ12SGMSGχ3400⟩ which represents the spin coupling can be expressed using Wigner's9j symbol [36]⟨χ13SG1MSG1χ24SG2MSG2|χ12SGMSGχ3400⟩=(−1)SG2+1[(2SG1+1)(2SG2+1)(2SG+1)]1/2×∑S,Ms⟨SG1MSG1;SG2MSG2|SMs⟩⟨SMs|SGMSG;00⟩{s1s3SG1s2s4SG2SG0S}.

(15) Here,
si is the spin of the gluongi , withi=1,2,3,4 , and∑S,Ms|SMs⟩⟨SMs| is the completeness relation.The helicity amplitude
MMJGMJG1MJG2 may be read off from⟨G1G2|T1|G⟩=δ3(KG1+KG2−KG)MMJGMJG1MJG21 ,

(16) allowing the
ηc→G1G2 decay width to be readily obtained [38]:Γ=π2|K|M2ηc∑JL|MJL|2 .

(17) Here,
MJL=MJL1M22EG ,M2 is the amplitude of theηc→gg reaction, andMJL1 is the partial wave amplitude, obtainable from the helicity amplitudeMMJGMJG1MJG21 via the Jacob-Wick formula [48], i.e.MJL1=√2L+12JG+1∑MG1,MG2⟨L0JMJG|JGMJG⟩×⟨JG1MJG1JG2MJG2|JMJG⟩MMJGMJG1MJG21

(18) with
J=JG1+JG2 andL=JG−J . -
In this section, we estimate the scalar and the pseudoscalar glueball production in
ηc andηb decays via the0++ model, by taking scalarsf0(1710) andf0(1500) , and pseudoscalarη(1405) as the corresponding candidates, namelyG1 andG2 respectively. The quantum numbers of the states involved in these processes are presented in Table 1;|G⟩ and|ηQ⟩ have the same quantum numbers.JPC 

L ML 

S MS 

ηQ 

0−+ 

1 

M0 

1 

−M0 

G1 

0++ 

0 

0 

0 

0 

G2 

0−+ 

1 

M2 

1 

−M2 

Table 1. Quantum numbers of
ηQ ,G1 , andG2 . The values ofM0 andM2 can be−1 ,0 , and1 . -
In Eq. (12), the color contraction is equal to eight, and for scalar glueballs, the spin and orbital angular momentum coupling causes the C-G coefficient to be
⟨00;00|00⟩=1 . Therefore, from these results, Eq. (12) can be rewritten as⟨G1G2|T1|G⟩=∑MG,MG28γg√8EGEG1EG2⟨1M0;1−M0|00⟩×⟨1M2;1−M2|00⟩×⟨χ1300χ241−M2|χ121−M0χ3400⟩IM0,0,M2(K).

(19) The spin coupling term
⟨χ1300χ241−M2|χ121−M0χ3400⟩ is characterized by the Wigner's9j symbol, a representation of4 -particle spin coupling, which can be expanded as series of2 -particle spin couplings represented by Wigner's3j symbols [36], shown in Appendix A.By substituting the spin couplings provided in Appendix A into Eq. (19), we can then reduce the
T1 matrix element,⟨G1G2|T1|G⟩=−16γg√8EGEG1EG2(|⟨11,1−1|00⟩|2I1,0,1(K)+|⟨10,10|00⟩|2I0,0,0+|⟨1−1,11|00⟩|2I−1,0,−1(K))=−γg18√8EGEG1EG2(I1,0,1(K)+I0,0,0(K)+I−1,0,−1(K)) .

(20) With a lengthy calculation (some details are given in Appendix B) the momentum space integrals are obtained, of which
I1,0,1=I−1,0,−1=0 , andI0,0,0 is given by Eq. (B8). Writingδ3(KG−KG1−KG2)I≡I0,0,0 and considering Eqs. (16), (20) and (B8), we have⟨G1G2|T1|G⟩=δ3(KG−KG1−KG2)MMJGMJG1MJG21=−γg18√8EGEG1EG2I0,0,0=−γg18√8EGEG1EG2δ3(KG−KG1−KG2) I ,

(21) from which
MMJGMJG1MJG21=M0001 can be extracted out, i.e.M0001=−γg18 I √8EGEG1EG2 .

(22) The probable radius R of the HO wavefunction is estimated by the relation
R=1/α , withα=√μω/ℏ . Here,μ denotes the reduced mass,ω is the angular frequency of the HO satisfyingM=(2n+L+3/2)ℏω , with M being the glueball mass, n the radial quantum number, and L the orbital angular momentum. As discussed in Refs. [49, 50], the effective mass of the constituent gluon is about0.6 GeV, which meansμ∼0.3 GeV for glueballs. In the calculation, the inputs we adopt are:Mηc=2.98 GeV,Mηb=9.40 GeV,Mf0(1500)=1.50 GeV,Mf0(1710)=1.71 GeV andMη(1405)=1.41 GeV [51]. Therefore, using the equations above, we can calculate the corresponding radii:Rηc=2.24GeV−1 ,Rηb=1.26GeV−1 ,Rf0(1500)=2.79GeV−1 ,Rf0(1710)=2.61GeV−1 andRη(1405)=3.26GeV−1 .With above discussion and inputs, we can readily get I and
M0001 . Please note that, when⟨L0JMJG|JGMJG⟩=⟨L0J0|00⟩=⟨0000|00⟩=1,

(23) ⟨JG1MJG1JG2MJG2|JMJG⟩=⟨0000|00⟩=1,

(24) M001 can be obtained according to Eq. (18), as shown in Table 2.I (GeV)−3/2 

M001 

ηc→f0(1500)η(1405) 

0.409 

−0.166γg 

ηb→f0(1500)η(1405) 

−0.398 

0.901γg 

ηb→f0(1710)η(1405) 

−0.396 

0.897γg 

Table 2. The I and
M001 values for different processes. -
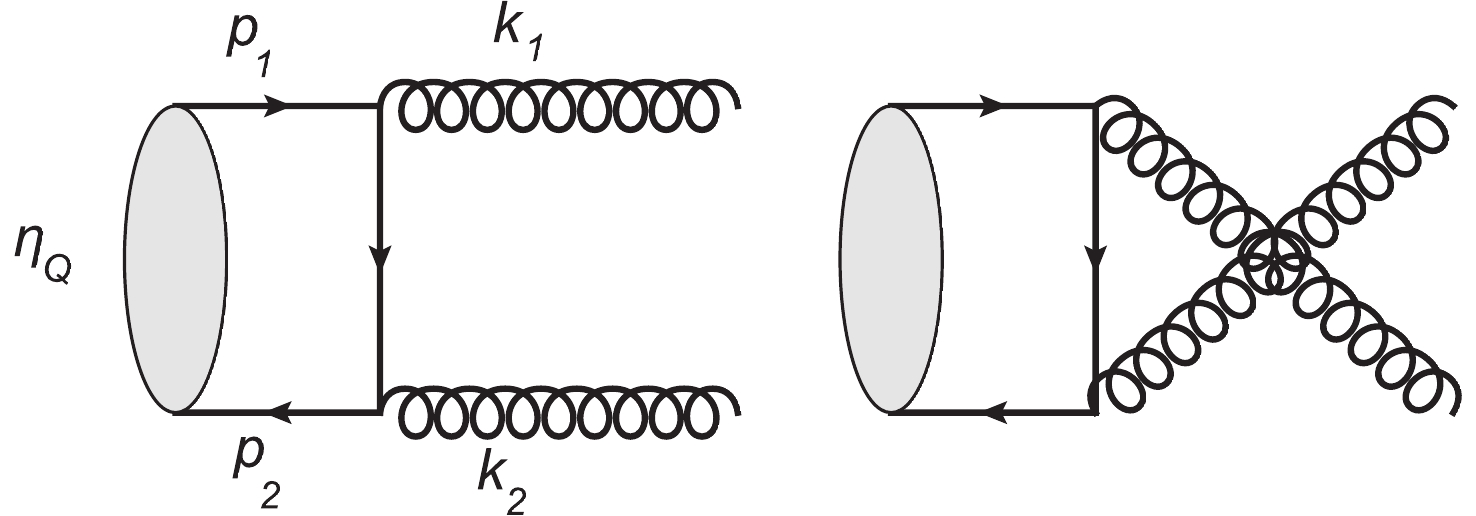
The calculation of the process
ηQ→gg is quite straightforward. At the leading order of perturbative QCD, there are only two types of decay paths, represented using Feynman diagrams in Fig. 3. Their decay amplitudes can be written as:iAμν,ab1ϵ∗μ(k1)ϵ∗ν(k2)=(igs)2ˉv(p2)γνtbip/1−k/1−mQ×γμtau(p1)ϵ∗μ(k1)ϵ∗ν(k2),

(25) iAμν,ab2ϵ∗μ(k1)ϵ∗ν(k2)=(igs)2ˉv(p2)γμtaip/1−k/2−mQ×γνtbu(p1)ϵ∗μ(k1)ϵ∗ν(k2),

(26) where u and
ˉv stand for heavy quark spinors,ϵμ denotes the gluon polarization, andgs is the strong coupling constant. For a quark pair to form a pseudoscalar quarkonium, one can realize it by performing the following projection [52]:u(p)ˉv(−p)→iγ5RηQ(0)2√2π×mQ(p/+mQ)⊗(1c√Nc) .

(27) Here,
mQ is the heavy quark mass,RηQ(0) denotes the radial wavefunction at the origin, and in aηQ center-of-mass systemp1=p2≡p . TheηQ→gg matrix element squared may be obtained through a straightforward calculation, i.e.|M2|2=4g4s|R(0)ηQ|23πmQ.

(28) -
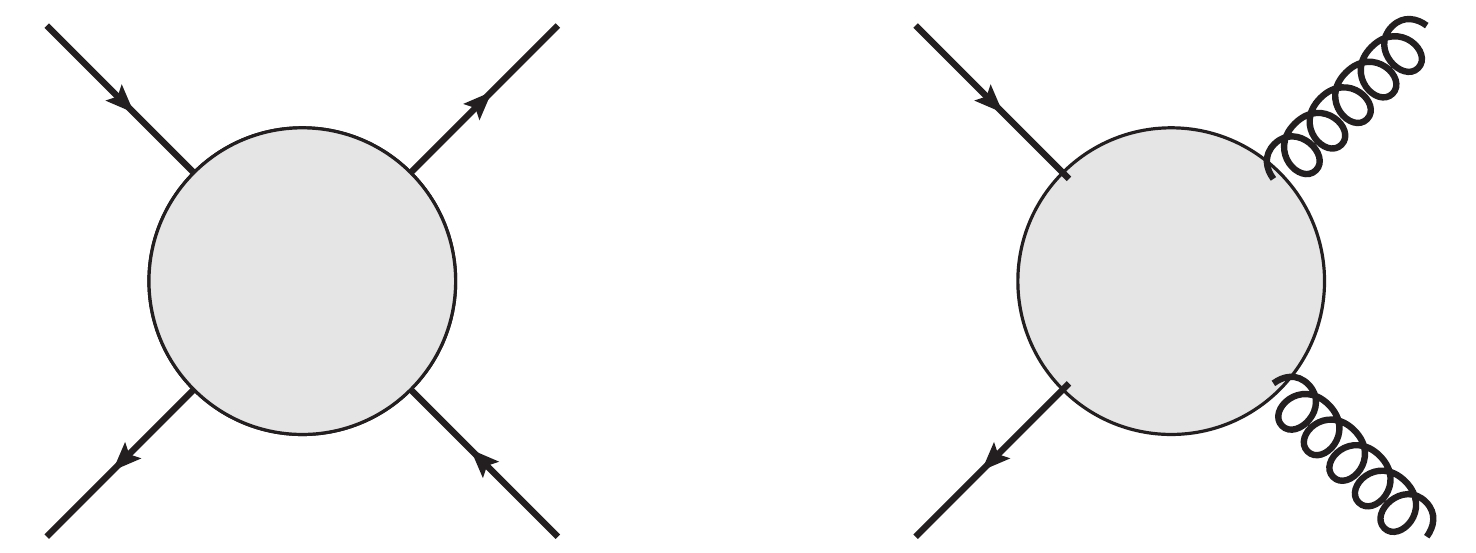
We estimate the strength of gluon-pair-vacuum coupling analogously to the
3P0 model, where the strength of quark pair creation in vacuum is represented byγq with dimensions of energy [40]. To avoid constructing a new model to mimic the nonperturbative process of the gluon pair production in the vacuum, we simply inferγg by comparing the relative strength of processesqˉq→gg andqˉq→qˉq , as shown in Fig. 4. The valueγ2g/γ2q is assumed to be the same order of magnitude as the relative interaction rate of these two processes.It is well known that at the tree level
|ˉM(qˉq→qˉq)|2=4g4s9(s2+u2t2+t2+u2s2−2u23st),

(29) |ˉM(qˉq→gg)|2=32g4s27(−9(t2+u2)4s2+tu+ut).

(30) Considering the relationship between Mandelstam variables, we find that
γ2g/γ2q≈σ(qˉq→gg)σ(qˉq→qˉq)≈(1.10±0.37)×10−2 ,

(31) where the interaction energy is set to be
μηc , the reduced mass of the quark− antiquark in the decaying meson. In the3P0 model,γq(μηc)=0.299×2mq√96π [40] withmq=220 MeV [39] the value of the light quark constituent mass. Hence we find thatγ2g(μηc)≈(5.74±1.93)×10−2 GeV2 . By the same method, we obtainγ2g(μηb)≈(2.57±0.86)×10−3 GeV2 . -
Using Eq. (4) and the relation
MJL=MJL1M22EG , we find thatMJL has only one nonzero matrix element,M001=−γg18I√8EGEG1EG2 , and that|M2|2=4g4s|R(0)ηQ|23πmQ . Substituting these values into Eq. (17), we can then calculate the decay width ofηc→f0(1500)η(1405) ,Γ=π2|K|M2ηc∑JL|MJL|2=π2|K|4M4ηc|M001|2|M2|2=2π2g4s|R(0)ηc|2γ2g|K|EGEG1EG2I235πmcM4ηc=27.41+11.02−10.12 keV.

(32) In the above calculation, we set the charm quark mass to be
mc=(1.27±0.03) GeV [51], strong coupling constant to beαs(ηc)=0.25 , and theηc radial wavefunction at the origin squared to be|R(0)ηc|2=0.527±0.013 GeV3 [52]. The branching fraction of theηc→f0(1500)η(1405) process is thenBrηc→f0(1500)η(1405)=Γηc→f0(1500)η(1405)Γtotal=8.62+3.77−3.32×10−4 .

(33) Analogous to the
ηc decay, theηb exclusive decay to glueball pairs can similarly be evaluated by the0++ model. We notice thatf0(1710) is glue rich [12, 53, 54], and evaluate the processηb→f0(1710)η(1405) as well. Using the same procedure as forηc , we haveΓηb→f0(1500)η(1405)=7.57+2.68−2.60 keV ,Brηb→f0(1500)η(1405)=7.57+9.50−4.26×10−4 ,

(34) Γηb→f0(1710)η(1405)=7.34+2.60−2.53 keV ,Brηb→f0(1710)η(1405)=7.35+9.23−4.14×10−4 .

(35) For these calculations, we took the bottom quark mass to be
mb=(4.18±0.03) GeV [51], the strong coupling constant to beαs(ηb)=0.18 , and theηb radial wavefunction at the origin squared to be|R(0)ηb|2=4.89±0.07 GeV3 [52]. It is worthwhile to mention that although there are mixings among thef0(1370) ,f0(1500) andf0(1710) states [12], they do not have significant influence on our calculation results.Moreover, from lattice QCD calculations [3-6, 26], we know that there might be scalar and pseudoscalar glueball candidates with masses of
1.75 GeV and2.39 GeV, respectively. For these potential glueball candidates, we can readily calculate the branching fractionΓηb→G0++G0−+=4.56+1.61−1.57 keV ,Brηb→G0++G0−+=4.56+5.72−2.56×10−4 .

(36) -
In this work, we analyzed the processes of exclusive glueball pair production in quarkonium decays by introducing a
0++ model. This model was employed to phenomenologically mimic the gluon-pair-vacuum interaction vertices and is applicable to studies of glueball and hybrid state production. It was assumed that a gluon pair is created homogeneously in space with equal probability. By virtue of the3P0 model, we formulated an explicit vacuum gluon-pair transition matrix and estimated the strength of the gluon-pair creation. We subsequently applied this method and the results for the calculation of theηc tof0(1500) η(1405) decay process, wheref0(1500) andη(1405) are respective scalar and pseudoscalar glueball candidates. We found that the decay width and branching fraction of this decay process are27.41 keV and8.62×10−3 respectively.In light of the
ηc decay, we also evaluated theηb→f0(1500)η(1405) andηb→f0(1710)η(1405) processes; using the same method, we found that the decay widths and branching fractions are7.57 keV and7.57×10−4 , and7.34 keV and7.35×10−2 , respectively. Having supposed that there exist heavier scalar and pseudoscalar glueballs with masses1.75 GeV and2.39 GeV, as per the lattice QCD calculation, we calculated that the corresponding decay width and branching fraction is4.56 keV and4.56×10−4 . Our results in this work indicate that glueball pair production in pseudoscalar quarkonium decays is marginally accessible in the presently running experiments BES III, BELLE II, and LHCb.It should be mentioned that the hadronic two-body decay modes of the scalar-isoscalar
f0(1370) ,f0(1500) andf0(1710) were investigated in Ref. [55], where the leading order processG0→G0G0 was also proposed, but neglected in the practical calculations. We believe that in future studies, the combination of the0++ model with the analysis in Ref. [55] would no doubt inform us further on the properties of glueballs and isoscalar mesons.Lastly, we acknowledge that the gluon-pair-vacuum coupling estimate here is quite premature, hence the estimation for pseudoscalar quarkonium exclusive decay to glueballs is far from accurate. However, qualitatively the physical picture of such a decay is reasonably sound. To make the
0++ mechanism trustworthy in a phenomenological study, or in other words to ascertain the coupling strength, an experimental measurement should first focus on theηc→η′(958)+f0(1500) process, since we know thatη′(958) is also a glue-rich object. With an increase in experimental measurements on glueball production and decay, this model will be refined, hence improving upon its predictability. Although the refining process of the model will no doubt require a copious amount of work, due to the importance of glueball physics, we believe this research avenue deserves further exploration.The authors are grateful to the anonymous reviewers' comments and suggestions, which are important and responsible for the completeness and improvement of the paper.
-
In Eq. (19), the Wigner's
3j and9j symbols are{j1j2jm1m2m}=(−1)j1−j2−m√2j+1⟨j1j2m1m2|j,−m⟩

(A1) and
{j1j2j12j3j4j34j13j24j}=∑m{j1j2j12m1m2m12}{j3j4j34m3m4m34}{j13j24jm13m24m}×{j1j3j13m1m3m13}{j2j4j24m2m4m24}{j12j34jm12m34m},

(A2) respectively. Applying them to Eq. (15) reduces the spin coupling term to
⟨χ1300χ241−M2|χ121−M0χ3400⟩=3∑S,MS⟨00;1−M2|SMS⟩⟨SMS|1−M0;00⟩{11011110S}.

(A3) In the above equation, evidently
⟨00;1−M2|SMS⟩ and⟨SMS|1−M0;00⟩ become nonzero only whenS=1 , which meansMS can be any of1 ,0 or−1 . Thus, the possible|SMS⟩ states are|1,−1⟩ ,|1,0⟩ , and|1,1⟩ . On the other hand,⟨00;1−M2|SMS⟩ and⟨SMS|1−M0;00⟩ will be zero unlessM0=M2=−MS .Given
M≡MS , Wigner's9j symbol can then be calculated as follows:{110111101}=∑M{110m1m30}{111m2m4−M}×{101M0−M}{111m1m2−M}×{110m3m40}{0110M−M}=19⟨1m1;1m3|00⟩⟨1m2;1m4|1M⟩⟨1M;00|1M⟩×⟨1m1;1m2|1M⟩⟨1m3;1m4|00⟩⟨00;1M|1M⟩.

(A4) Provided only the transverse polarization exists, every term in the above equation can be evaluated by a normal C-G coefficient. That is,
⟨1m1;1m3|00⟩=√12(δm11δm3,−1−δm1,−1δm31) ,

(A5) ⟨1M;00|1M⟩=√22 ,

(A6) ⟨00;1M|1M⟩=√22 ,

(A7) ⟨1m3;1m4|00⟩=√12(δm31δm4,−1−δm3,−1δm41),

(A8) ⟨1m2;1m4|1−1⟩=0 ,

(A9) ⟨1m1;1m2|1−1⟩=0 ,

(A10) ⟨1m2;1m4|10⟩=√22(δm21δm4,−1−δm2,−1δm41) ,

(A11) ⟨1m1;1m2|10⟩=√22(δm11δm2,−1−δm1,−1δm21) ,

(A12) ⟨1m2;1m4|11⟩=0 ,

(A13) ⟨1m1;1m2|11⟩=0 .

(A14) After inserting the above results into Eq. (A3), we discover there is only one nonzero spin coupling
⟨χ1300χ2410|χ1210χ3400⟩=148(δm11δm3,−1−δm1,−1δm31)(δm31δm4,−1−δm3,−1δm41)×(δm21δm4,−1−δm2,−1δm41)(δm11δm2,−1−δm1,−1δm21),

(A15) which equals
−148 form1=−1 ,m2=1 ,m3=1 ,m4=−1 orm1=1 ,m2=−1 ,m3=−1 ,m4=1 , and0 for all other cases. -
For a non-trivial situation, that is
M0=M2=−M , the momentum integralIMLG,MLG1,MLG2(K) in Eq. (20) reduces toIM,0,M(K)=∫d3k1d3k2d3k3d3k4δ3(k1+k2)δ3(k3+k4)×δ3(KG1−k1−k3)δ3(KG2−k2−k4)×ψ∗n100(k1,k3)ψ∗n21M(k2,k4)ψn01M(k1,k2)Y00(k3−k42) .

(B1) Provided the ground state dominance holds, namely the principal numbers
n0 ,n1 , andn2 are equal to1 , the wavefunctionψ then turns toψ100(k)=1π3/4R3/2exp(−R2k22) ,

(B2) ψ11M(k)=i√2π3/4R5/2kMexp(−R2k22) ,

(B3) where
kM ,k±1=∓(kx±iky)/√2 , andk0=kz are the spherical components of the vectork .Integrating out those dummy variables, we can simplify Eq. (B1),
IM,0,M(K)=δ3(KG−KG1−KG2)∫d3k1ψ1∗100(k1,K−k1)×ψ2∗11M(−k1,−K+k1)ψG11M(k1,−k1)Y00(k1).

(B4) In addition, in the
ηQ center-of-mass system which impliesKG=KηQ=0 andKG1=−KG2=K , the spatial wavefunctions given in (B2) and (B3) may be written asψ1∗100=R3/21π3/4exp(−R21(2k1−K)28) ,

(B5) ψ2∗11M=−iR5/22√2π3/4(2k1−K)M exp(−R22(2k1−K)28) ,

(B6) ψG11M=i√2R5/20π3/4(k1)M exp(−R20(k1)22) ,

(B7) with
Y00=1√4π . Here,R0 ,R1 , andR2 are the most probable radii ofηc ,f0(1500) , andη(1405) , respectively. After performing the integration, one finds that the statesM=1 andM=−1 do not make any contribution to the total value, i.e.I1,0,1=I−1,0,−1=0 , whileI0,0,0=−δ3(KG−KG1−KG2)R3/21R5/22R5/206√2π5/4(R20+R21+R22)9/2×exp(−K2R20(R21+R22)8(R20+R21+R22))×{R20(R21+R22)[K4(R21+R22)2−96]+12R40[K2(R21+R22)−4]−12(R21+R22)2[K2(R21+R22)+4]}.

(B8)
Gluon-pair-creation production model of strong interaction vertices
- Received Date: 2019-10-07
- Accepted Date: 2020-05-23
- Available Online: 2020-09-01
Abstract: By studying the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: