Nucleon effective mass splitting and density-dependent symmetry energy effects on elliptic flow in heavy ion collisions at E_lab= 0.09 ~ 1.5 GeV/nucleon

The in-medium nucleon effective mass, initially introduced by Brueckner, exerts a large impact on numerous aspects in nuclear physics and astrophysics [1–4]. Various definitions for the nucleon effective mass are provided in the literature [5–8], where the non-relativistic effective mass and relativistic Dirac mass are two popular scenarios. Different definitions of the nucleon effective mass may have different physical content. From a non-relativistic point of view, the nucleon effective mass characterizes either the momentum (k-mass) or the energy (E-mass) dependence of the single-particle potential. Meanwhile, the relativistic Dirac mass is defined through the nucleon scalar self-energy in the Dirac equation. In the present study, we focus on the nucleon effective k-mass, which has been widely discussed in the heavy-ion collision community [2–4, 9–14]. The nucleon effective k-mass can be defined from the momentum dependence of the single-particle potential $U_{n,p}(p,\rho,\delta)$ in a nuclear medium with density ρ and isospin asymmetry $\delta = (\rho_{n}-\rho_{p})/\rho$ via $m^{*}/m = [1+\frac{m }{p} \frac{\partial U(p,\rho,\delta) }{\partial p} ]^{-1}$. Numerous theoretical approaches predicted that proton and neutron single-particle potential $U_{n,p}(p,\rho,\delta)$ is different in the isospin asymmetric nuclear medium, which leads to the neutron-proton effective mass splitting $m_{n-p}^{*}$ = $\frac{m_{n}^{*}-m_{p}^{*}}{m}$.

Heavy-ion collisions (HICs) provide a unique opportunity to explore the $m_{n-p}^{*}$ and the nuclear symmetry energy, as nuclear medium with different densities and isospin asymmetries can be created during collision [15–23]. Usually, transport models that often incorporate phenomenological potentials as an input are applied to deduce $m_{n-p}^{*}$ and symmetry energy from experimental observables. Although the effects of $m_{n-p}^{*}$ on various observables in HICs have been widely studied using different transport models, uncertainties in the effective mass splitting and especially its density dependence remain an open challenge for further research [2–4]. For example, by comparing the transverse neutron and proton spectra from central $^{124}{\rm{Sn}}+^{124}{\rm{Sn}}$ collisions with the Boltzmann-Langevin transport model, the effective mass of neutrons being lower than that of protons ($m_{n}^{*}<m_{p}^{*}$) is favored [24]. Later on, with the newly measured data from both $^{124}{\rm{Sn}}+^{124}{\rm{Sn}}$ and $^{112}{\rm{Sn}}+^{112}{\rm{Sn}}$ collisions and simulations with the improved quantum molecular dynamics (ImQMD-Sky) model, calculations with SLy4 ($m_{n}^{*}<m_{p}^{*}$) were found to lie close to the experimental data [25]. Calculations from the other two QMD-type models also indicated that results with $m_{n}^{*}<m_{p}^{*}$ are significantly closer to the experimental data [26, 27]. However, with the isospin-dependent Boltzmann-Uehling-Uhlenbeck transport model, calculated results were found to be lower than the newly measured data [28]. Furthermore, with the analysis of the nucleon-nucleon elastic scattering data based on the optical model and recent constraints on the nuclear symmetry energy based on the Hugenholtz-Van Hove theorem, the mass splitting $m_{n}^{*}>m_{p}^{*}$ is preferred [29]. Furthermore, in view of the present status of transport model comparisons, results on commonly used observables in HICs are not always the same, even if the same physical input is required in different transport models [20, 30, 31]. Thus, a more systematical and detailed study of the effects of $m_{n-p}^{*}$ on various observables is necessary.

This paper is organized as follows: in the following section, the ultra-relativistic quantum molecular dynamics (UrQMD) model and the isospin- and momentum-dependent potential are introduced. Sec. 3 presents and discusses effects of the nuclear symmetry energy and neutron-proton effective mass splitting on the elliptic flow of protons and neutrons produced from $^{197} {{\rm{Au}}}$ + $^{197} {{\rm{Au}}}$ collisions at beam energies from 0.09 GeV/nucleon to 1.5 GeV/nucleon. Finally, a summary is provided in Sec. 4.

In the UrQMD model, each hadron is represented by a Gaussian wave packet with the width of $\sigma^2 =$ 2 ${\rm fm}^2$ for $^{197} {{\rm{Au}}}$ in the phase space [32–38]. The centroid ${{r}}_{i}$ and ${{p}}_{i}$ are propagated according to the Hamiltonian equations of motion via:

Here, H depicts the n-body total Hamiltonian of the system, which consists of the kinetic energy and the effective potential energy V. Within the present code, the potential energy V is composed of the Coulomb potential energy, local potential energy, and isospin- and momentum-dependent potential energy,

The Coulomb potential energy can be written as

Here, $r_{ij}$ is the distance between the i-th and the j-th charged particles. The ${\rm erf}$ is the error function, which is written as erf(t) = $\dfrac{2}{\sqrt{\pi}}\int_{0}^{t}{\rm e}^{-x^{2}}{\rm d}x$.

The local potential energy $V_{{\rm{loc}}}$ can be obtained with $V_{{\rm{loc}}}(\rho) = \int u_{{\rm{loc}}}{\rm d}{{r}}$. Here, $u_{{\rm{loc}}}$ is provided by the Skyrme potential energy density functional [35, 39]

Taking the isospin effects into consideration [40–43], the momentum-dependent potential energy $V_{{\rm{mom}}}$ can be written as $V_{{\rm{mom}}} = \int u_{{\rm{mom}}} {\rm d}{{r}}$, where

Here, $v({{p}},{{p}}^{\prime }) = 0.00157 \ln^{2}[1+500 ({{p}}-{{p}}^{\prime })^{2}]$ was widely used in QMD-like models [44]. Along with $\alpha = -396.4$ MeV, $\beta = 331.8$ MeV, and $\gamma = 1.14$, a soft equation of state can be obtained for the isospin symmetric nuclear matter with the compressibility K = 200 MeV. ${g}_{\rm{sur}}$ = 18.2 MeV fm² and ${g}_{\rm{sur,iso}}$ = 8.9 MeV fm² are employed, as in our previous study [37], to prevent the initialized nuclei disintegration. By setting x = $\pm0.6$, one can obtain different neutron and proton effective masses. For example, x = 0.6 represents $m_{n}^{*}<m_{p}^{*}$, while x = –0.6 represents $m_{n}^{*}>m_{p}^{*}$. $f_{\tau}$ is the phase-space density. For infinite nuclear matter at zero temperature, $f_{\tau}$ can be written as a step function $f_{\tau}({{r}},{{p}})$ = $\dfrac{2}{h^{3}}\Theta(p_{F_{\tau}}-p)$, in which $p_{F_{\tau}}$ is the Fermi momenta of baryons. They can be written as $p_{F_{n}} = \hbar c\left(\dfrac{3\pi^{2}\rho}{2}\right)^{\frac{1}{3}}\left(1+\delta\right)^{\frac{1}{3}}$, $p_{F_{p}} = \hbar c\left(\dfrac{3\pi^{2}\rho}{2}\right)^{\frac{1}{3}}\left(1-\delta\right)^{\frac{1}{3}}$, and $p_{F} = \hbar c\left(\dfrac{3\pi^{2}\rho}{2}\right)^{\frac{1}{3}}$.

In the mean field approximation, the above potential energy density yields the following single-particle potential:

The nucleon effective mass $m^{*}$ in nuclear medium is defined as

$m_0$ = 0.938 GeV/c² denotes the free mass. The effective mass as a function of momentum is plotted in Fig. 1.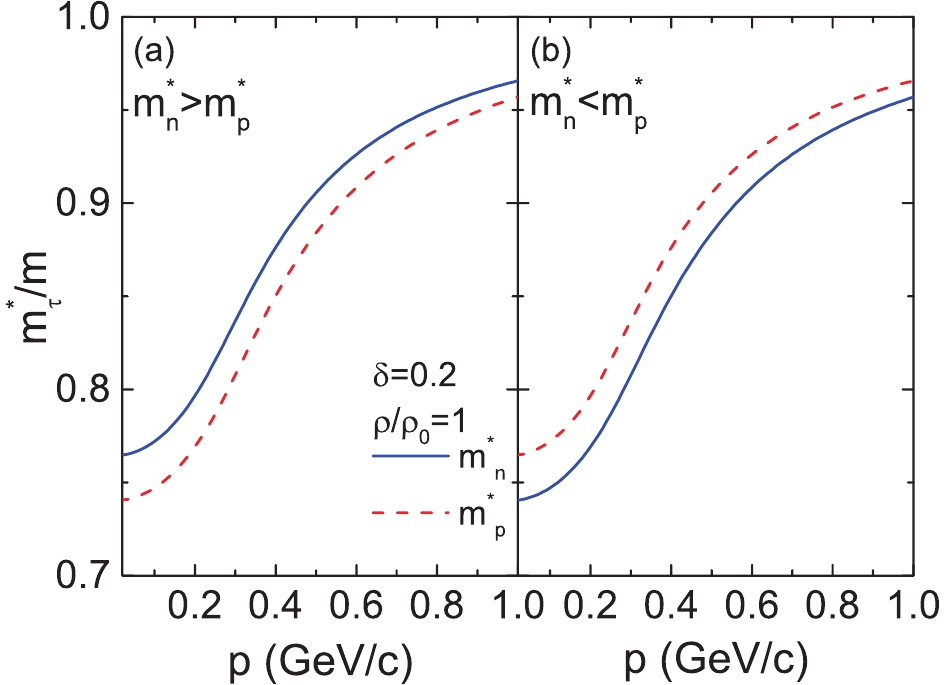

Figure 1.  (color online) Effective mass of neutron and proton as a function of momentum at $\delta = 0.2$ and $\rho = \rho_0$.

The energy per nucleon $E(\rho,\delta)$ of the isospin asymmetric nuclear matter, can be written as

Within the parabolic approximation ($E(\rho,\delta) = E(\rho,0) +$$E_{\rm sym}(\rho)\delta^{2} + {\cal{O}}(\delta^{4})$), which is widely used in the literature, the symmetry energy can be written as the following three parts,

The nuclear symmetry energy $S_0$ = $E_{\rm{sym}}(\rho_0)$ and its slope $L = 3\rho_{0}\frac{\partial E_{\rm{sym}}(\rho)}{\partial\rho}|_{\rho = \rho_{0}}$ at the saturation density are displayed in Table 1. The density dependence of nuclear symmetry energy with different parameter sets is shown in Fig. 2. To investigate the effect of $m_{n-p}^{*}$ on the elliptic flow in HICs, we need to minimize the impact of the nuclear symmetry energy. Thus, two parameter sets with different $m_{n-p}^{*}$, which correspond to almost the same density-dependent nuclear symmetry energy $E_{\rm{sym}}(\rho)$, are employed. Furthermore, parameter sets with the same $m_{n-p}^{*}$ but different $E_{\rm{sym}}(\rho)$ are also considered. Three different $E_{\rm{sym}}(\rho)$ given by SKz4, SKM*, and SV-sym34 interactions are also shown for comparison.

Para	$a_{\rm sym}$	$b_{\rm sym}$	${S}_{0}$	L	$m_n^*$	$m_p^*$
asy-hard ($m_{n}^{*} < m_{p}^{*}$)	5.6	8.0	31.0	108.8	0.81	0.84
asy-hard ($m_{n}^{*} > m_{p}^{*}$)	11.5	9.8	31.0	106.8	0.84	0.81
asy-soft ($m_{n}^{*} < m_{p}^{*}$)	30.6	−17.0	31.0	33.8	0.81	0.84
asy-soft ($m_{n}^{*} > m_{p}^{*}$)	36.5	−15.3	31.0	31.8	0.84	0.81

Table 1.  Saturation properties of nuclear matter as obtained with selected parameters of this study. Effective proton and neutron masses are calculated for neutron-rich nuclear matter at $\delta = 0.2$ and ρ = $\rho_{0}$ = 0.16 fm⁻³.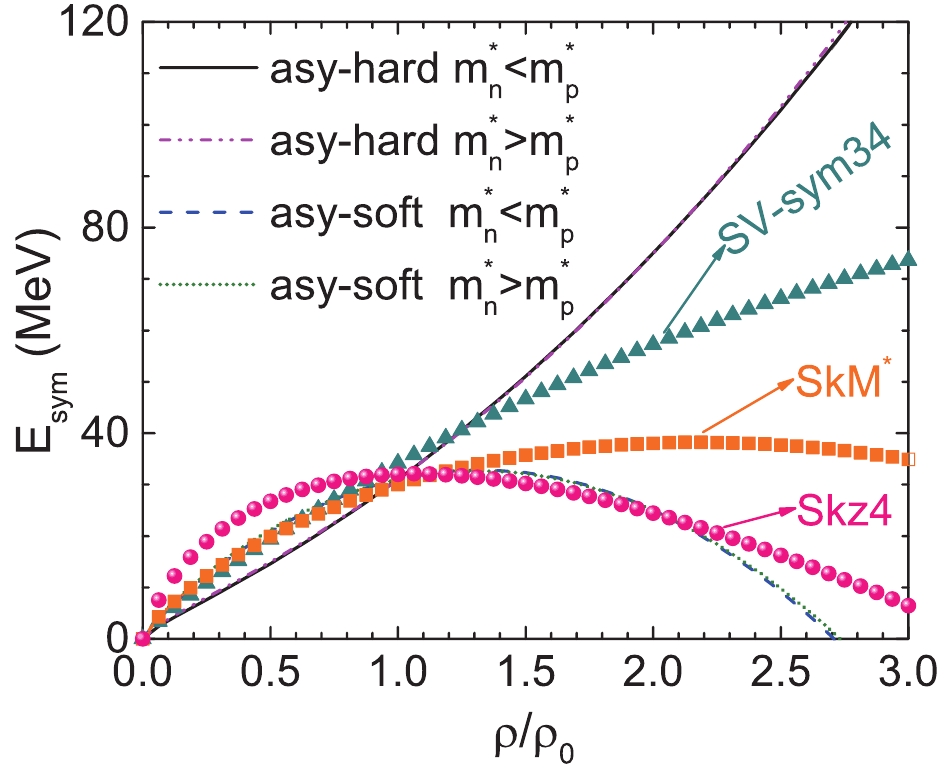

Figure 2.  (color online) Density dependence of nuclear symmetry energy. Lines depict symmetry energies incorporating isospin- and momentum-dependent interaction (iso-MDI). Symmetry energies (i.e., Skz4, SkM*, and SV-sym34) used in a previous UrQMD model [35, 36] incorporating the isospin-independent momentum-dependent interaction (MDI) are also shown for comparison.

In this study, 600000 events for $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions are simulated for each case. At the end of the reaction, fragments are recognized by employing the isospin-dependent minimum span tree (iso-MST) algorithm. By this method, if the relative distances and momenta of two nucleons are smaller than $R_{0}$ and $P_{0}$, respectively, they are considered to belong to the same fragment. With a proper set of $R_{0}$ and $P_{0}$, the fragment mass distribution in HICs at intermediate energies is efficiently reproduced [45–47]. The parameters adopted in this study are $R_{0}^{pp}$ = 2.8 fm, $R_{0}^{nn}$ = $R_{0}^{np}$ = 3.8 fm, and $P_{0}$ = 0.25 GeV/c. Notably, the collective flow was insensitive to reasonable ranges of $R_{0}$ and $P_{0}$ [35].

The collective flow in HICs was studied extensively to deduce properties of formed hot and dense matter. In this study, we focus on the elliptic flow $v_{2}$, which is the second-order coefficient in the Fourier expansion of the azimuthal distribution of emitted particles, $v_2 = \left \langle \frac{p_x^2-p_y^2}{p_t^2} \right \rangle$. Here, $p_x$ and $p_y$ are two components of the transverse momentum $p_t = \sqrt{p_x^2+p_y^2}$, and the angular bracket denotes an average over all considered particles from all events. Usually, for a certain species of particles generated in the nuclear reaction with a fixed collision system, beam energy, and impact parameter, $v_2$ depends on both the rapidity $y_z$ and the transverse momentum $p_t$. The scaled units $y_0\equiv y/y_{\rm{pro}}$ and $u_{t0}\equiv u_t/u_{\rm{pro}}$ (the transverse component of the four-velocity) are used instead of $y_z$ and $p_t$ throughout, as in the experiments [48]. The subscript $pro$ denotes the incident projectile in the center-of-mass system.

Figure 3 shows the rapidity dependence of $v_{2}$ of protons in semi-central $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at beam energies 0.4 GeV/nucleon (in plot (a)) and 0.6 GeV/nucleon (in plot (b)) with the cut $u_{t0}>0.4$. The calculated results are in a good agreement with the experimental data at both beam energies, especially at mid-rapidities. As expected, the effects of both the $E_{\rm{sym}}(\rho)$ and the $m_{n-p}^{*}$ on $v_{2}$ of protons are quite weak, because the isospin-dependent component of the nuclear interaction is relatively small compared to the isoscalar one when the isospin asymmetry is not too large. To highlight the effects of the nuclear symmetry energy and $m_{n-p}^{*}$, the elliptic flow ratio or difference between isospin partners (such as neutron and proton, $^{3}{\rm{H}}$ and $^{3}{\rm{He}}$) are utilized. Fig. 4 shows the elliptic flow ratio $v_{2}^{n}/v_{2}^{p}$ at mid-rapidity($\left|y_{0}\right|<0.2$) as a function of the slope parameter of the $E_{\rm sym}(\rho)$. To compare the elliptic flow calculated with the neutron-proton effective mass splitting to that without the splitting, $v_{2}^{n}/v_{2}^{p}$ is shown, calculated with $E_{\rm{sym}}(\rho)$ given by the three Skyrme interactions in combination with an isospin-independent (without nucleon effective mass splitting) form of the momentum dependent term $V_{md}$ = 1.57 [ln (500(Δp)²+1)]²ρ/$\rho_0$. First, the increase of $v_{2}^{n}$/$v_{2}^{p}$ with L was reported and discussed in Refs. [36, 45, 49–52]. The nuclear symmetry potential tends to expel neutrons, whereas it attracts protons in a neutron-rich environment. The repulsion for neutrons (attraction for protons) is significantly stronger for the hard, rather than the soft, symmetry energy at densities above $\rho_0$. Second, the $v_{2}^{n}/v_{2}^{p}$ obtained with effective mass splitting $m_{n}^{*}<m_{p}^{*}$ are larger than those with $m_{n}^{*}>m_{p}^{*}$, while calculations with the previous UrQMD version, where the isospin-independent form of momentum-dependent potential is used (without effective mass splitting), lie in between the results obtained with $m_{n}^{*}<m_{p}^{*}$ and $m_{n}^{*}>m_{p}^{*}$. This is attributed to nucleons with a smaller effective mass experiencing a larger repulsive force (leading to a stronger elliptic flow) than those with a larger effective mass. This finding is consistent with results from the LQMD model and the microscopic stochastic mean-field (SMF) model, although different forms of momentum-dependent symmetry potentials were used [9, 53–55]. However, this is different from the results presented in Refs. [43, 56, 57], where an improved IQMD model was employed. This might result from different contributions of the density- and momentum-dependent components of the nuclear symmetry energy in each model. Third, we observe that the $E_{\rm{sym}}(\rho)$ has a relatively larger influence than $m_{n-p}^{*}$ on the $v_{2}^{n}/v_{2}^{p}$ with the present parameter sets, i.e., the difference in the slopes of the two $E_{\rm{sym}}(\rho)$ is approximately 75 MeV, and the variation of $m_{n-p}^{*}$ ranges from –0.03 to 0.03 at $\delta = 0.2$ and ρ = 0.16 fm^-3. It is reasonable to infer that with a larger variation in $m_{n-p}^{*}$ (or with a smaller variation of the slope L), the $E_{\rm{sym}}(\rho)$ and the $m_{n-p}^{*}$ may contribute similarly to $v_{2}^{n}/v_{2}^{p}$. Furthermore, we note that the influence of $m_{n-p}^{*}$ on the $v_{2}^{n}/v_{2}^{p}$ is less evident with the stiff $E_{\rm{sym}}(\rho)$ than that with the soft one. This is because the contribution of the momentum-dependent component to the symmetry potential is smaller than that of the density-dependent component in the case of stiff symmetry energy, whereas in the soft case, the momentum-dependent component plays a more important role than the density-dependent component on $v_{2}^{n}/v_{2}^{p}$.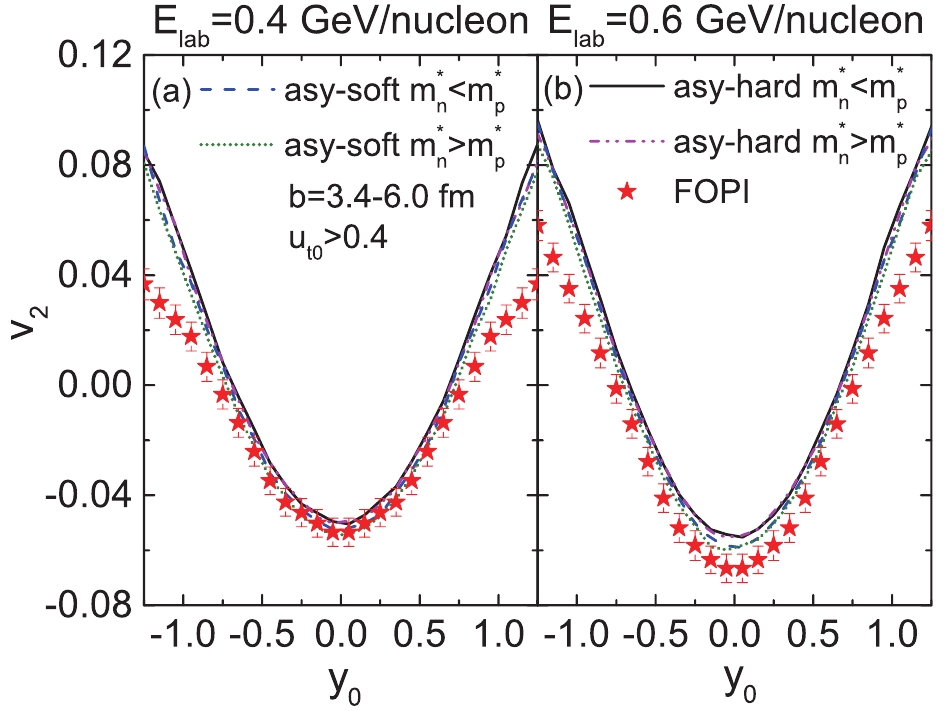

Figure 3.  (color online) Elliptic flow $v_{2}$ of protons in semicentral (3.4 < b < 6.0 fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at ${E}_{\rm lab}$ = 0.4 GeV/nucleon (a) and 0.6 GeV/nucleon (b) as a function of the reduced rapidity ${y} _{0}$. The cut $u_{t0}>0.4$ is chosen as the cut. Calculated results with two symmetry energies along with two different $m_{n-p}^{*}$ are presented by different lines. FOPI experimental data (stars) is provided by Ref. [48].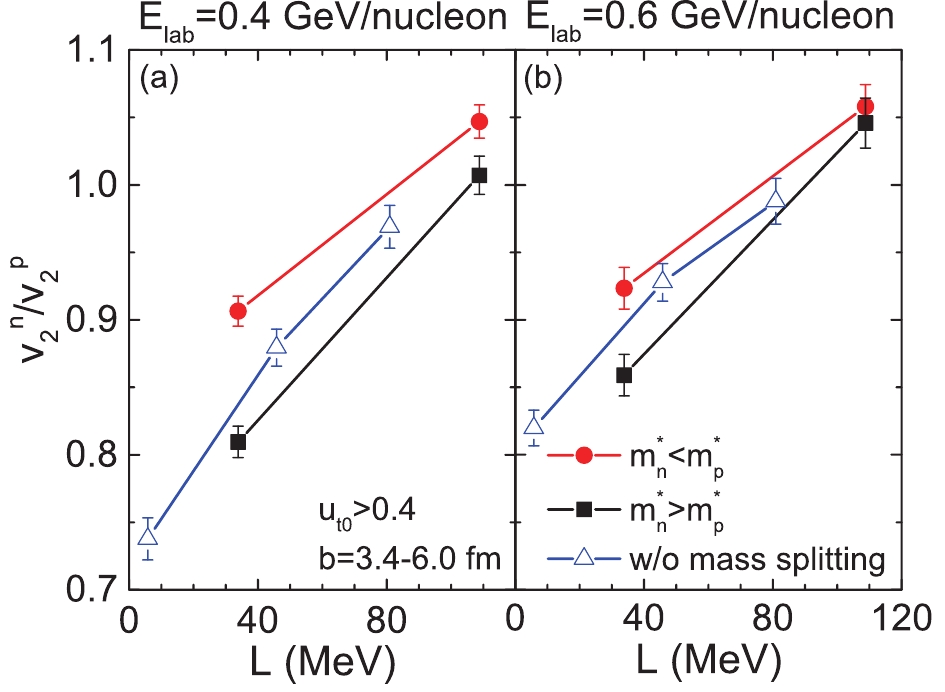

Figure 4.  (color online) Elliptic flow ratio between free neutrons and protons $v_{2}^{n}$/$v_{2}^{p}$ at mid-rapidity ($\left|y_{0}\right|<0.2$) produced in semi-central (3.4 < b < 6.0 fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at beam energies 0.4 (left panel) and 0.6 (right panel) GeV/nucleon as a function of the slope parameter L. $v_{2}^{n}/v_{2}^{p}$ values calculated with the previous UrQMD model, without consideration of the effects of $m_{n-p}^{*}$ are shown by open symbols.

The elliptic flow of free protons at mid-rapidity ($\left|y_{0}\right|<0.4$) as a function of the transverse velocity $u_{t0}$ is displayed in Fig. 5. The calculated results are in line with the FOPI experimental data, and the difference among different parameter sets is very small. To more clearly reveal the effects of $E_{\rm{sym}}(\rho)$ and $m_{n-p}^{*}$ on the $v_2$, the elliptic flow difference between free neutrons and protons $v_{2}^{n}$-$v_{2}^{p}$ is displayed in Fig. 6. The results are found to fall roughly into two distinct groups: the results with soft symmetry energies and those with stiff symmetry energies. The values of $v_{2}^{n}$-$v_{2}^{p}$ obtained with hard symmetry energies are smaller than those with soft symmetry energies. This is attributed to the harder symmetry energy yielding a stronger repulsive (attractive) potential for neutrons (protons) in the neutron-rich system, which leads to a more negative $v_2$ for neutrons, consequently a larger value of $v_{2}^{n}$-$v_{2}^{p}$. These findings are consistent with many previous studies [36, 49–52]. We establish once more that the impact of the $m_{n-p}^{*}$ on $v_{2}^{n}$–$v_{2}^{p}$ is more evident with the soft, rather than stiff, symmetry energy.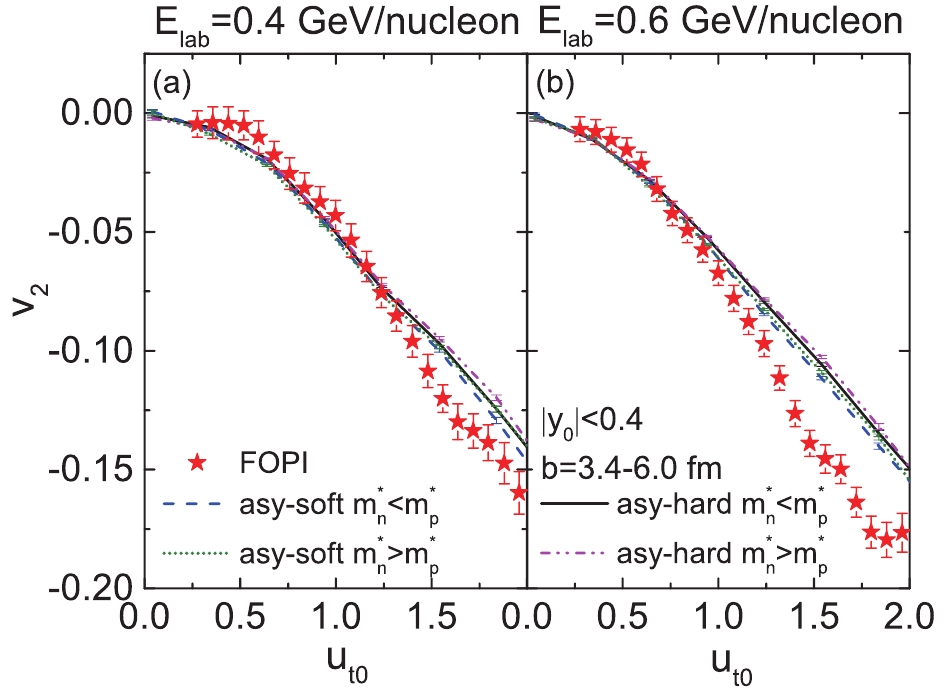

Figure 5.  (color online) Normalized transverse velocity $u_{t0}$ dependence of $v_{2}$ of free protons produced in semi-central (3.4 < b < 6.0 fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at beam energies 0.4 (a) and 0.6 (b) GeV/nucleon. Rapidity cut $\left|y_{0}\right|<0.4$ is chosen to be the same as in FOPI experimental data from Ref. [48].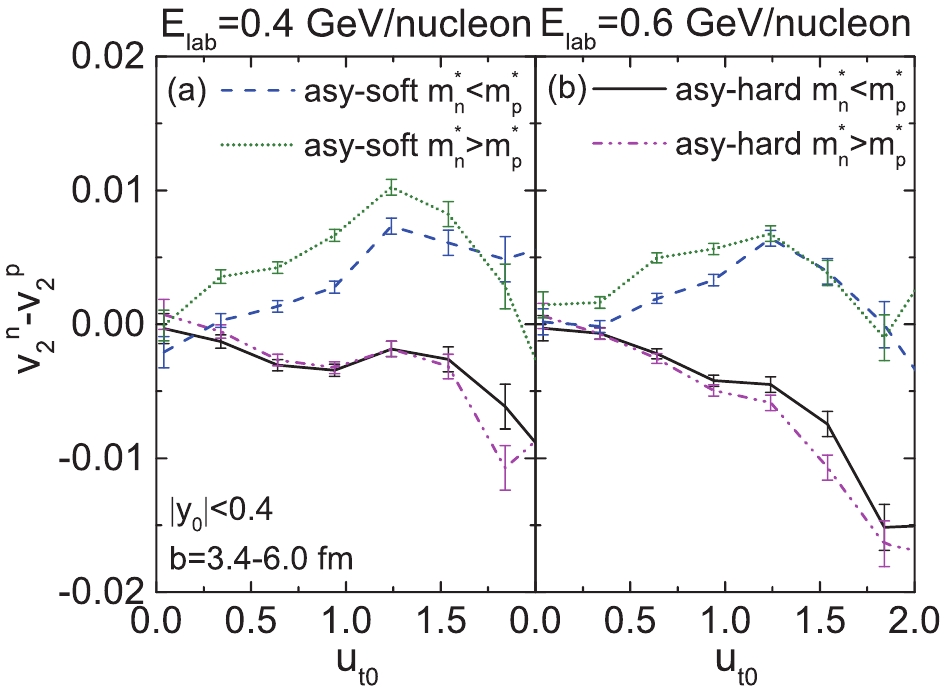

Figure 6.  (color online) Elliptic flow difference of free neutrons and free protons generated in semi-central ($3.4<b<6.0$ fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at beam energies 0.4 (a) and 0.6 GeV/nucleons (b) as a function of $u_{t0}$ with rapidity windows $\left|y_{0}\right|<0.4$.

Higher density nuclear matter can be created in HICs with higher beam energies, as displayed in the upper panel of Fig. 7, where the nuclear density at the central region in Au+Au collisions at various beam energies is plotted as a function of the reaction time. The central density reaches 2$\rho_0$ and 3$\rho_0$ at beam energies of 0.4 GeV/nucleon and 1.5 GeV/nucleon, respectively. The duration of the high density phase is gradually shortened by increasing the beam energy. To reveal the environment density of the free nucleons (which are recognized at the end of the reaction) experienced during the collision, the density profiles of free nucleons are traced back to t = 5, 10, 15, 20 fm/c and displayed in the lower panel of Fig. 7. At t = 10–15 fm/c (the moment of maximum compression stage at ${E}_{\rm lab}$ = 1.0 GeV/nucleon), most free nucleons (that are recognized at the end of the reaction) are located in an environment with a density larger than the saturation density. During this period, the momentum transfer is very large because of the nucleon-nucleon collision and high pressure. At t = 15 fm/c, the system begins to expand rapidly and the momentum of free nucleons are already close to their final values [58]. In addition, by applying rapidity and transverse velocity cuts, the selected nucleons will fly from the high-density to the low-density region and become free very rapidly, so as to only weakly interact with other nucleons after t = 15 fm/c. Accordingly, the elliptic flow of free nucleons can reflect high-density behavior of the mean-field potential.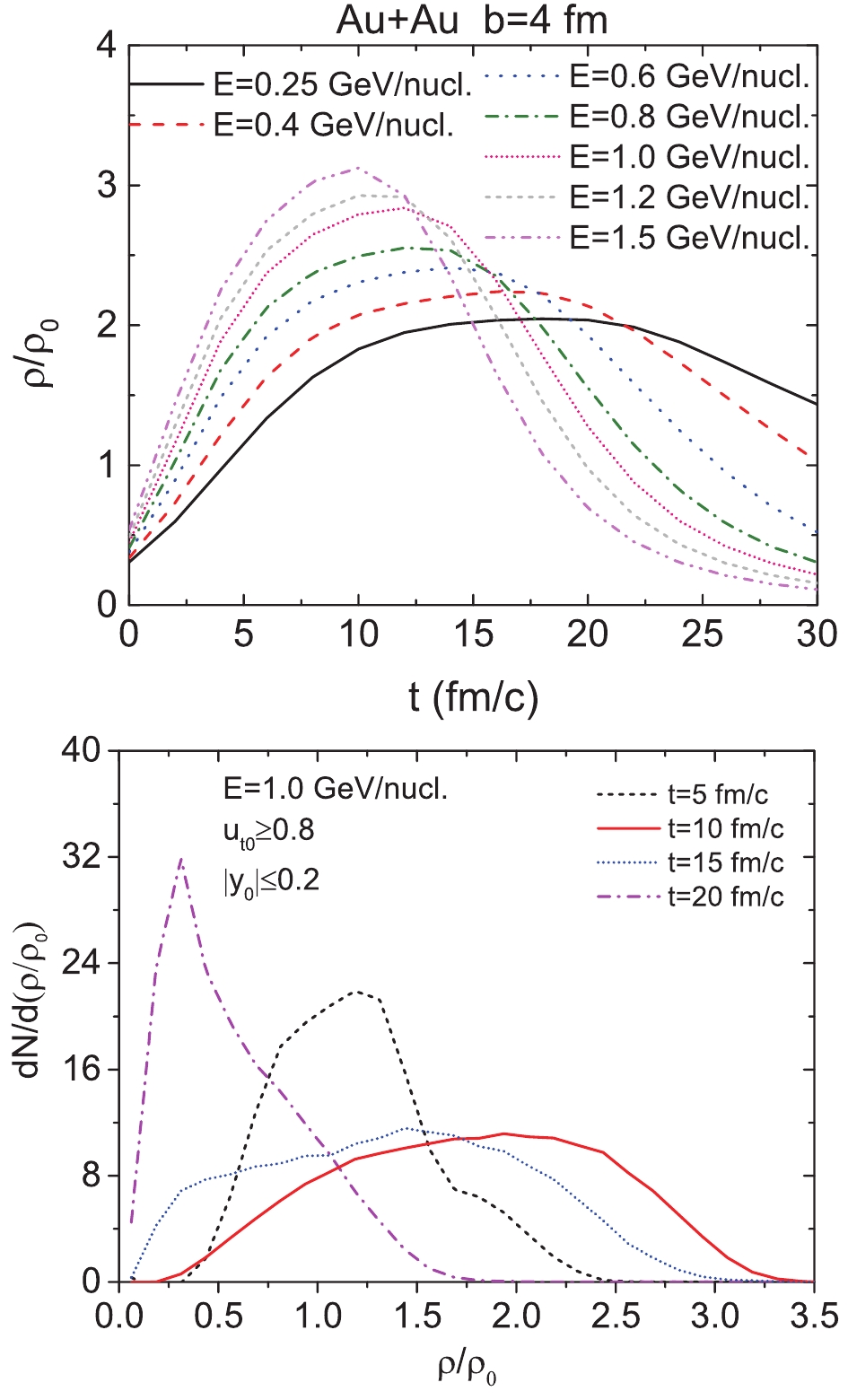

Figure 7.  (color online) Evolution of nuclear density with respect to time at central region (origin of coordinates) in Au+Au collisions with b = 4 fm and various beam energies (upper panel). Density profile of nucleons recognized as free nucleons at end of reaction (lower panel). Results from ${E} _{\rm lab}$ = 1.0 GeV/nucleon and at t = 5, 10, 15, 20 fm/c are displayed as an example.

It has been widely discussed that the elliptic flow ratio (difference) between neutrons and protons at mid-rapidity reflects the high density behavior of the nuclear symmetry energy [36, 45, 49–52]. On the one hand, the impact of $E_{\rm{sym}}(\rho)$ and the $m_{n-p}^{*}$ on observables is expected to be more pronounced at higher energies than at lower energies, because a larger difference exists at higher densities. On the other hand, the influence may be suppressed because of the more violent collisions at higher energies. To more systematically illustrate the influence of the $E_{\rm{sym}}(\rho)$ and $m_{n-p}^{*}$ on $v_{2}$ in a larger range of beam energy, the elliptic flow of free protons and neutrons, as well as their difference $v_{2}^{n}$–$v_{2}^{p}$ are plotted in Figs. 8 and 9, respectively, as a function of beam energy from 0.09 to 1.5 GeV/nucleon. The FOPI data of elliptic flow of free protons at mid-rapidity ($\left|y_{0}\right|$$\leqslant 0.2$) is reproduced fairly well. The elliptic flow first decreases to a minimum value at about 0.6 GeV/nucleon, then steadily increases with the beam energy. This phenomenon has been extensively studied and discussed, e.g., Refs. [58, 59]. The negative $v_2$ at intermediate energies originates from the fact that the presence of spectator matter leads to more nucleons emitted out of the plane. With further increase in the beam energy, $v_2$ increases to a positive value at the beam energy around 5 GeV/nucleon, because the spectator matter passes through the interaction region rapidly and no longer blocks expansion of the compressed matter [60]. At beam energies $\leqslant 0.15$ GeV/nucleon, $v_2$ becomes positive, which represents a preferential in-plane emission (rotational-like). Fig. 9 shows that with present variation ranges of $m_{n-p}^{*}$ and the symmetry energy slope parameter L, the impact of $E_{\rm{sym}}(\rho)$ is comparable to that of $m_{n-p}^{*}$ on $v_{2}^{n}$-$v_{2}^{p}$ at beam energies $\leqslant 0.25$ GeV/nucleon. Meanwhile, at higher beam energies, $E_{\rm{sym}}(\rho)$ has a stronger influence on $v_{2}^{n}-v_{2}^{p}$ than $m_{n-p}^{*}$. The main reason is that the contribution of the momentum-dependent component to the symmetry potential may be comparable to that of the density-dependent component at lower beam energies (lower density). With increasing beam energy, nuclear matter with higher densities and more energetic nucleons is produced, and the contribution from the density-dependent component may be more pronounced because of the near equivalence of the free and effective masses at the higher relative momenta prevailing at higher beam energies. Moreover, the impact of both $E_{\rm{sym}}(\rho)$ and $m_{n-p}^{*}$ on $v_{2}^{n}-v_{2}^{p}$ is gradually weakened by the increase of beam energy, as the mean field effects are weakened in more violent collisions occurring at higher energies. Thus, beam energies within $0.6 \sim 1.0$ GeV/nucleon are suggested to probe the $E_{\rm{sym}}(\rho)$, especially at supranormal densities, because the neutron-proton effective mass splitting effect is relatively weak, whereas the symmetry energy effect is remains significant.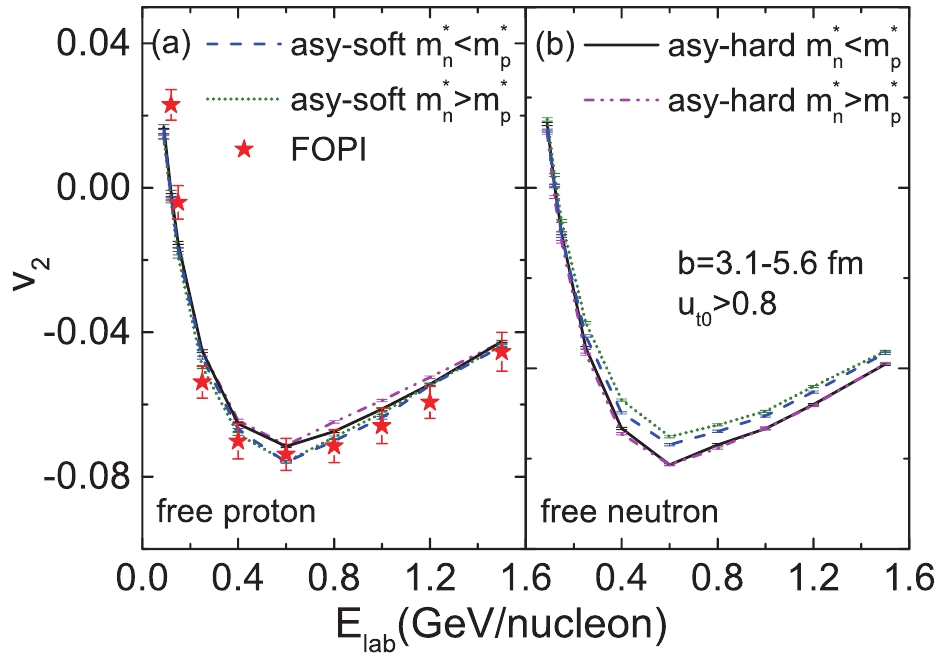

Figure 8.  (color online) Beam energy dependence of elliptic flow of free protons (a) and neutrons (b) at mid-rapidity ($\left|y_{0}\right|$$\leqslant 0.2$) from semicentral ($3.1\leqslant$b$\leqslant 5.6$ fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions. $u_{t0}$$\geqslant 0.8$ is chosen to be same as in FOPI experimental data provided by Ref. [58].

Figure 9.  (color online) Excitation function of elliptic flow difference between free neutrons and protons $v_{2}^{n}$-$v_{2}^{p}$ in semi-central ($3.1 \leqslant$b$\leqslant 5.6$ fm) $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions with $u_{t0}$$\geqslant 0.8$ cut.

The effects of the neutron-proton effective mass splitting $m_{n-p}^{*}$ and the density-dependent symmetry energy $E_{\rm{sym}}(\rho)$ on the elliptic flow in $^{197}{\rm{Au}}+^{197}{\rm{Au}}$ collisions at beam energies of 0.09-1.5 GeV/nucleon are investigated within the UrQMD model. The FOPI data of elliptic flow of free protons at mid-rapidity ($\left|y_{0}\right|$$\leqslant 0.2$) is reproduced fairly well. With present parameter sets, i.e., where the difference in the slopes of the two $E_{\rm{sym}}(\rho)$ is approximately 75 MeV, and the variation of $m_{n-p}^{*}$ ranges from –0.03 to 0.03 at saturation density of $\delta = 0.2$, at a lower beam energy ($\leqslant 0.25$ GeV/nucleon), the elliptic flow difference between neutrons and protons $v_{2}^{n}-v_{2}^{p}$ is sensitive to both the $E_{\rm{sym}}(\rho)$ and the $m_{n-p}^{*}$, and their influences are comparable with each other. Meanwhile, at higher beam energy ($\geqslant 0.25$ GeV/nucleon), the $v_{2}^{n}-v_{2}^{p}$ is more sensitive to $E_{\rm{sym}}(\rho)$ than $m_{n-p}^{*}$. To distinguish these two effects, we suggest that the high transverse-momentum particles from peripheral collisions may serve as a potential probe, as observables (e.g., elliptic flow) at high impact parameters and transverse momenta are sensitive to the momentum dependence of the mean-field potential [61]. Furthermore, the impact of $m_{n-p}^{*}$ on $v_{2}^{n}-v_{2}^{p}$ is more evident in the parameter set with the soft, rather than the stiff, symmetry energy. Beam energies within $0.6 \sim 1.0$ GeV/nucleon are suggested to probe the density-dependent symmetry energy at supranormal densities, as the neutron-proton effective mass splitting effect is relatively weak, whereas the symmetry energy effect remains significant.

The authors acknowledge support by the computing server C3S2 in Huzhou University.